今天给大家带来的是清华大学、阿里巴巴和蚂蚁集团共同发表于Usenix Security'23的工作. 更多内容请查看原文.
Abstract
本文专注于诚实大多数假设下面向二进制电路的恶意安全三方计算方案. 先前最优的方案是Boyle等人[7]在CCS'19给出的, 其均摊通信效率与CCS'16上Araki等人[3]给出的半诚实方案相同, 但具有较大的计算开销: 与Furukawa等人[21]在Eurocrypt'17提出的实现结果相比, 其通信开销是Araki等人方案的9倍, 但计算比Furukawa等人的方案慢约4.5倍. 本文通过Boneh等人在Crypto'19提出的分布式零知识证明来验证\(\mathbb{F}_2\)上计算的正确性, 并利用素数域的代数结构使得协议对传统CPU计算是友好的. 实验结果表明, 当面向AES电路时, 本文协议计算效率比Boyle等人的方案快3.5倍. 当应用于恶意安全的DNN推理中的二进制运算(如比较和截断)时, 本文所提方案可降低67%的计算时间. 此外, 本文还发现了现有概率截断协议中存在的一个安全性问题. 本文代码在Github开源: malicious_3pc_binary
Introduction & Contributions
诚实大多数假设下的三方计算(至多一方被腐化)由于其高效性和实用性备受关注, 但在恶意安全设定下, 腐化方可任意偏离协议, 使其实现高效率变得更具有挑战性, 特别是对于计算二进制电路而言. 先前的代表性工作有:
- 基于复制秘密共享的[2, 21]
- 遵循Beaver乘法三元组方法的[4]
- 依赖于cut-and-choose范式生成可验证AND三元组的[13]
[21]需要每方需要通信10比特来计算一个AND门, [2]通过取更小的桶进一步优化为每方仅需通信7比特, 但需要额外进行洗牌(shuffle). 尽管如此, 与目前最优的半诚实安全方案[3]相比(每方每个AND门仅需通信1比特), 这些方案在恶意安全下仍需要7倍的通信开销. Boyle等人[7]利用分布式零知识证明探索了一种不同的实现恶意安全的方法[6], 在均摊方式下, 每方计算每个AND门仅需1比特通信. 然而, 分布式零知识证明要求底层的计算域的足够大以满足可靠性(soundness)误差可忽略不计.
对于二进制电路的特殊情况, [7]的协议必需将数据的计算从二元域\(\mathbb{F}_2\)提升到扩域\(\mathbb{F}_{2^\kappa}\)(其中\(\kappa\)是安全参数), 这带来了巨大的计算开销, 严重影响协议的计算效率. [21]的协议大多数计算在\(\mathbb{F}_2\)上进行, 通信方面的节省使其在LAN设定下的计算时间减慢4.5倍, 也有利于其在WAN设定下的计算.
本文提出并回答了如下问题:
能否为二进制电路构造具有恶意安全性的高效三方计算协议, 使其通信复杂度符合半诚实安全协议[3], 同时具有与基于cut-and-choose方法[2, 21]相当的具体效率?
本文主要贡献如下:
Efficient 3PC for Binary Circuits with Malicious Security
本文通过使用分布式零知识证明在\(\mathbb{F}_2\)上设计高效的验证协议, 可看成是[7]的一个变种. 与基于扩域的方法[6, 7]相比, 本文所提方案具有亚线性的通信开销和轮复杂度, 以及更低的计算开销. 其提升主要原因如下:
-
与[7]中使用\(\mathbb{F}_{2^\kappa}\)不同, 本文提出在分布式零知识证明中使用素数域\(\mathbb{F}_p\)来验证二进制计算, 其中\(p=2^{61}-1\)为梅森素数. 这是由于在\(\mathbb{F}_{2^\kappa}\)上的算术运算比在大小相当的\(\mathbb{F}_p\)上的算术运算效率低. 然而, 将\(\mathbb{F}_{2^\kappa}\)上计算验证转化为\(\mathbb{F}_p\)上的验证并非易事, 本文给出了降低转换过程开销的方法, 使得在\(\mathbb{F}_p\)中需要验证的乘法次数仅为\(\mathbb{F}_{2^\kappa}\)的2倍.
-
本文利用素域的代数结构来进一步优化分布式零知识证明的计算复杂度. 标准的分布式零知识技术验证\(\mathbb{F}_p\)上\(m\)个乘法三元组的正确性需要的计算复杂度为\(\mathbb{F}_p\)上的\(O(m)\)个运算. 本文将AND三元组转换为\(\mathbb{F}_p\)上的乘法三元组, 展示了如何将\(\mathbb{F}_p\)上的大部分计算降低到\(\mathbb{F}_2\)上. 此外, 利用素数域的代数结构, 本文使用按位XOR和AND运算对计算进行批处理, 这对CPU计算时非常高效且友好的.
Applications to Maliciously Secure DNN Inference
在PPML中, 通常使用二进制电路计算比较、截断等非线性运算更有效. 本文使用MP-SPDZ框架实现了一个恶意安全的三方DNN推理的混合协议. 结果表明, 本文的协议在二进制部分获得恶意安全性的开销减少了67%以上. 与基于cut-and-choose的方法[21]相比, 本文协议不仅降低了9倍通信复杂度, 而且实现了更快的运行时间.
A Security Issue in Probabilistic Truncation Protocols
本文的一个额外发现是, 发现现有的概率截断协议中存在隐藏的安全问题, 其根本原因是使用相同的随机性来保护被截断秘密值的隐私, 并为截断值概率采样1比特舍入误差. 这在考虑多方交互的消息和协议输出的联合分布时是有问题的. 因此, 当需要使用精确截断协议时, 不得不引入更多的二进制门.
Preliminaries
Secret Sharing
本文是诚实大多数假设下的三方计算场景, 三方记为\(P_0,P_1,P_2\), 恶意敌手至多腐化1个参与方, 涉及两种秘密共享方案:
- 加法秘密共享(ASS)
- 复制秘密共享(RSS): 记秘密\(x\)在环\(\mathbb Z_{2^k}\)上的RSS方案为\([\![x]\!]^R=(x_0,x_1,x_2)\). 类似地, 记\([\![x]\!]^B\)为\(x\)在\(\mathbb{F}_2\)上的RSS方案, \([\![x]\!]^F\)为\(x\)在\(\mathbb{F}_p\)上的RSS方案.
Distributed Zero-Knowledge Proofs
为了实现恶意安全, 本文协议的关键在于秘密共享数的零知识证明. GMW协议指出, 将半诚实安全协议编译为恶意安全协议的方法是强制使用零知识证明来执行半诚实行为, 即要求每方提供一个零知识证明及其消息, 以证明该消息是根据半诚实协议如实计算得到的. 对于基于秘密共享的协议来说, 这样的声明(statement)在各方之间进行分发, 即声明的输入(如, 消息)在各方之间进行秘密共享. 本文采用分布式零知识证明[6]来实现恶意安全.
分布式零知识技术建立在完全线性证明(fully linear proofs)之上. 本文所依赖的主要底层技术是基于完全线性概率可检证明(fully linear probabilistic checkable proof, FLPCP)构造的完全线性交互预言证明(fully linear interactive oracle proof, FLIOP). 这一证明系统在有限域上工作且要求域的大小要足够大(因为可靠性要求误差正比于域大小的逆). 它采用递归的方法在每一轮中将电路规模减半, 并在下一轮将减半电路的评估再次委托给证明者. 在经过对数轮后, 电路规模减小到最小, 验证者可以直接对电路进行评估从而完成验证. 总体而言, FLIOP达到了对数级别的证明大小和轮复杂度, 本文将使用FLIOP来降低二进制计算的验证成本.
Ideal Functionalities
本文协议涉及如下理想功能:
- \(\mathcal{F}_\mathrm{rand}\): 生成随机份额, 可通过安全PRF实例化.
- \(\mathcal{F}_\mathrm{coin}\): 为所有参与方生成随机值\(r\), 可通过调用\(\mathcal{F}_\mathrm{rand}\)生成随机秘密值\(r\)的份额, 然后向所有参与方打开\(r\)来实例化;
- \(\mathcal{F}_\mathrm{input}\): 生成参与方的输入在\(\mathbb F_2\)上的安全分享, 协议的实例化方式如下:

Maliciously Secure 3PC for Binary Circuits
[7]中的整个恶意安全3PC协议工作原理可总结为:
- 运行基于RSS的半诚实安全协议;
- 调用检验的理想功能\(\mathcal{F}_\mathrm{vrfy}\)检查半诚实计算的正确性.
这里的理想功能\(\mathcal{F}_\mathrm{vrfy}\)用于验证各方发送的用于计算乘法门的消息的正确性. 本文中同样运用这一理想功能来检查各方执行AND计算的正确性.

在[7]中, 为在二进制电路中实例化\(\mathcal{F}_\mathrm{vrfy}\), 半诚实计算中涉及的数需要从\(\mathbb{F}_2\)提升到足够大的扩域\(\mathbb{F}_{2^\kappa}\)上(以保证可忽略的可靠性误差), 然后直接应用基于FLIOP的零知识证明[6]. 本文注意到这在计算上开销很大, 因此本文试图寻找一种有效的方法将\(\mathbb{F}_2\)上的半诚实计算转化为素数域\(\mathbb{F}_p\)上的计算.
The Overall Protocol: Achieving Malicious Security
为了将半诚实安全协议提升到恶意安全, [7]已经表明, 足以验证半诚实计算中各方的诚实行为. 在[7]中抽象出\(\mathcal{F}_\mathrm{vrfy}\)来检验各方发送的用于计算乘法门的消息的正确性. 在处理二进制电路时, \(\mathcal{F}_\mathrm{vrfy}\)检查AND门计算中各方消息的正确性. 下面介绍其在二进制电路中的工作原理.
给定\([\![x]\!]^B\)和\([\![y]\!]^B\), 为计算AND, \(P_i\)持有随机性\(\alpha_i=\rho_i\oplus\rho_{i-1}\), 其中\(\rho_i\)和\(\rho_{i-1}\)是由RPF和预分享的密钥生成的. \(P_i\)首先计算如下公式
\[z_i=x_i\cdot y_i\oplus x_i\cdot y_{i-1}\oplus x_{i-1}\cdot y_i\oplus \alpha_i,\tag1 \]然后发送给\(P_{i+1}\).
为了验证\(P_i\)的诚实行为, 理想功能\(\mathcal{F}_\mathrm{vrfy}\)需要在该电路的每个AND门检验\(z_i\)的正确性. 给定\(\mathcal{F}_\mathrm{vrfy}\), 本文按照[7]的方法构造了针对恶意敌手的安全计算二进制电路的协议. 具体来说, 在半诚实计算结束后的验证阶段, 每一方都充当证明者, 其他方充当验证者调用\(\mathcal{F}_\mathrm{vrfy}\)检验证明者消息的正确性.
完整协议过程如下:

Instantiating \(\mathcal{F}_\mathrm{vrfy}\) - Verifying AND Computations
为验证\(P_i\)的行为, 参与方需要电路中每个AND门检查公式\((1)\)是否成立, 其中证明者\(P_i\)持有输入份额\((x_i,x_{i-1})\), \((y_i,y_{i-1})\), 输出份额\(z_i\), 关联随机性\((\rho_i,\rho_{i-1})\). 关键之处在于在公式\((1)\)中, 每个变量由\(P_i\)和\(P_{i+1}\)或者\(P_i\)和\(P_{i-1}\)持有, 两个验证者\(P_{i-1}\)和\(P_{i+1}\)需要利用自己与证明者共有的部分数据来检验公式\((1)\)的关系是否成立.
分布式零知识证明[6]天然适用于这种数据在单个证明者和多个验证者之间共享的证明任务. 然而, [6]的证明系统要求底层的有限域足够大以达到可忽略的可靠性误差, 这种关系不适用于\(\mathbb{F}_2\), 如果将\(\mathbb{F}_2\)提升到\(\mathbb{F}_{2^\kappa}\)再进行验证, 则计算成本很高. 为了解决这个问题, 本文中将验证任务转换到素数域\(\mathbb{F}_p\), 如此仅涉及具有模运算的整数计算, 从而可达到减少分布式零知识证明计算开销的目的.
Step 1: Reduce the Relation
首先考虑一个AND门的情况, 定义公式\((1)\)中如下新变量:
\[a:=x_i,c:=y_i,e:=x_i\cdot y_i\oplus z_i\oplus\rho_i,\\ b:=y_{i-1},d:=x_{i-1},f:=\rho_{i-1}.\tag{2} \]其中, \(P_i,P_{i+1}\)已知\(a,c,e\), 而\(P_i,P_{i-1}\)已知\(b,d,f\). 因此, 验证公式\((1)\)归结为验证如下公式\((3)\):
\[a\cdot b\oplus c\cdot d\oplus e\oplus f=0.\tag3 \]Step 2: Transform to Prime Fields
下面将公式\((3)\)的关系从\(\mathbb{F}_2\)转换到\(\mathbb{F}_p\), 而不是提升到\(\mathbb{F}_{2^\kappa}\).
关键: 将\(\mathbb{F}_2\)上的每个值视为\(\mathbb{F}_p\)上的值, 然后通过域运算模拟\(\mathbb{F}_2\)上的XOR和乘法, 主要利用如下等式:
对于\(a,b\in\{0,1\}\)和\(p\geq3\), 有\(a\oplus b=a+b-2ab\bmod p=p(1-2b)+b\bmod p\).
根据公式\((3)\), 有
\[\begin{aligned} &a\cdot b\oplus c\cdot d\oplus e \oplus f\\ =&(a\cdot b\oplus e)\oplus (c\cdot d\oplus f)\\ =&(a\cdot b\cdot(1-2e)+e)\oplus (c\cdot d\cdot(1-2f)+f)\\ =&(a\cdot b\cdot(1-2e)+e)+(c\cdot d\cdot(1-2f)+f)-2(a\cdot b\cdot(1-2e)+e)\cdot(c\cdot d\cdot(1-2f)+f)\bmod p\\ =&-2(a\cdot c\cdot(1-2e))\cdot(b\cdot d\cdot(1-2f))+(c\cdot(1-2e))\cdot(d\cdot(1-2f))+(a\cdot(1-2e))\cdot(b\cdot(1-2f))-\\ &\frac{1}{2}((1-2e)\cdot(1-2f))+\frac{1}{2}\bmod p, \end{aligned}\notag \]其中, \(\frac{1}{2}\)表示\(2\)在\(\mathbb{F}_p\)上的逆元. 简单起见, 下文中省略\(\bmod p\). 由于\(P_i,P_{i+1}\)已知\(a,c,e\), 而\(P_i,P_{i-1}\)已知\(b,d,f\), 故有:
- \(P_i,P_{i+1}\)可本地计算\(g_1:=-2a\cdot c\cdot(1-2e)\), \(g_2:=c\cdot(1-2e)\), \(g_3:=a\cdot(1-2e)\), \(g_4:=-(1-2e)/2\);
- \(P_i\), \(P_{i-1}\)可本地计算\(h_1:=b\cdot d\cdot(1-2f)\), \(h_2:=d\cdot(1-2f)\), \(h_3:=b\cdot(1-2f)\), \(h_4:=1-2f\).
如此, 只需在\(\mathbb{F}_p\)上验证如下等式\((4)\):
\[\sum_{k=1}^4g_k\cdot h_k+\frac{1}{2}=0.\tag4 \]Step 3: Batch Verifying Multiple AND Gates
现在可以通过将基于FLIOP的分布式零知识证明系统[6]直接应用于评估整个电路时进行的所有AND计算来检验\(P_i\)的行为的正确性. 然而, 在[6, 7]中的第一步是通过乘以随机系数将\(m\)个内积关系转化为单个长度为\(4m\)的内积关系. 这样做是为了减少对单个内积关系的检查, 随机系数保证了如果原来的内积关系中有一个不正确, 那么得到的内积关系有压倒性的概率是不正确的. 但在本文的情况下不需要乘以随机系数, 这是因为若存在某个AND三元组使得公式\((1)\)不成立(意味着\(P_i\)计算AND门时偏离了协议), 则有\(\sum_{k=1}^4g_k\cdot h_k+1/2=a\cdot b\oplus c\cdot d\oplus e\oplus f=1\).
假设有\(m\)个AND三元组\(\{[\![x^{(\ell)}]\!]^B,[\![y^{(\ell)}]\!]^B,[\![z^{(\ell)}]\!]^B\}_{\ell=1}^m\)需要验证, 对于所有\(\ell\in[m]\), 若\(P_i\)遵循协议, 则有\(\sum_{k=1}^4g_k^{(\ell)}\cdot h_k^{(\ell)}+1/2=0\), 否则有\(\sum_{k=1}^4g_k^{(\ell)}\cdot h_k^{(\ell)}+1/2=1\). 下面考虑在\(\mathbb{F}_p\)上的总和:
\[\sum_{\ell=1}^m(\sum_{k=1}^4g_k^{(\ell)}\cdot h_k^{(\ell)}+\frac{1}{2}),\notag \]显然它等于\(P_i\)不遵循协议计算的AND门数量. 当\(m<p\)时, 若存在一个AND门, \(P_i\)没有遵循协议, 则有\(\sum_{\ell=1}^m(\sum_{k=1}^4g_k^{(\ell)}\cdot h_k^{(\ell)}+{1}/{2})\neq 0\), 这符合检验的需求. 此外, 容易看出这一技巧在\(\mathbb{F}_{2^\kappa}\)不能使用, 因为只要偶数个AND三元组不正确, 错误将被抵消.
因此, 若选择的素数域\(\mathbb{F}_p\)满足\(p>m\), 则只需简单验证如下关系:
\[\sum_{\ell=1}^m(\sum_{k=1}^4g_k^{(\ell)}\cdot h_k^{(\ell)}+\frac{1}{2})=0.\tag5 \]现在重新排列变量并定义如下两个长为\(4m\)的向量:
- \(\vec{u}:=(g_1^{(1)},g_2^{(1)},g_3^{(1)},g_4^{(1)},\cdots,g_1^{(m)},g_2^{(m)},g_3^{(m)},g_4^{(m)})\).
- \(\vec{v}:=(h_1^{(1)},h_2^{(1)},h_3^{(1)},h_4^{(1)},\cdots,h_1^{(m)},h_2^{(m)},h_3^{(m)},h_4^{(m)})\).
如此, 公式\((5)\)可以写成
\[\sum_{k=1}^{4m}u_k\cdot v_k=-\frac{m}{2}.\tag6 \]这样就把检验\(m\)个长为4的内积关系转化为在\(\mathbb{F}_p\)上检验1个长为\(4m\)的内积关系.
定理1: 设素域\(\mathbb{F}_p\)足够大, 在Setup步骤中, 随机性由伪随机函数生成. 协议C.2.1在\(\mathcal F_\mathrm{coin}\)-混合模型中存在一个恶意方的情况下, 实现具有(计算)中止安全的\(\mathcal F_\mathrm{vrfy}\), 其统计误差以\(\dfrac{2\lambda(\log_\lambda m+1)+1}{p-\lambda-1}\)为界.
Step 4: Applying Distributed Zero-Knowledge Proofs
下面遵循基于FLIOP的分布式零知识证明使各方在\(\mathbb{F}_p\)上检验公式\((6)\)是否成立. 本文通过引入压缩参数\(\lambda\)进行递归, 推广了基于FLIOP构造的分布式零知识证明系统. 内积关系通过插值转化为多项式方程, 然后以递归的方式, 在每一轮中将证明任务的大小以\(\lambda\)为因子进行压缩, 直到达到最小的大小, 验证者进行简单的最终检验来判定证明的正确性.
Step 4.1: Transform to Polynomials
需要证明的是公式\((6)\). 令\(m':=4m\), 定义一个计算长度为\(m'\)的内积电路\(C\), 包含\(m'\)个乘法门, 并将它们的输出求和. 定义\(\mathsf{out}:=-\frac{m}{2}\), 表示当输入为\(\vec{u}\)和\(\vec{v}\)时电路的输出, 即
\[\sum_{k=1}^{m'}u_kv_k=\mathsf{out}.\tag7 \]现在转而用多项式来表示这种关系, 将\(m'\)个乘法门排列成\(s\)组, 每组由\(\lambda\)个乘法门组成. 对\(k\in[\lambda]\), \(t\in[s]\), 第\(t\)组的第\(k\)个乘法门取左输入为\(u_{(t-1)\lambda+k}\)和右输入为\(v_{(t-1)\lambda+k}\). 对于每一组\(t\), 将输入导线上的值插值为一个多项式. 具体来说, 定义多项式\(p_1(X),\cdots,p_s(X)\)对应于左输入导线的值, \(q_1(X),\cdots,q_s(X)\)为右输入导线的值, 使得对\(t\in[s]\), \(k\in[\lambda]\), 有如下\(\lambda-1\)阶多项式:
\[p_t(k)=u_{(t-1)\lambda+k}, \qquad q_t(k)=v_{(t-1)\lambda+k}.\tag8 \]则可以通过定义如下多项式\(G(X)\)编码电路的输出:
\[G(X)=\sum_{t=1}^sp_t(X)\cdot q_t(X).\tag9 \]显然有
\[\sum_{k=1}^\lambda G(k)=\sum_{k=1}^\lambda\sum_{t=1}^sp_t(k)\cdot q_t(k)=\sum_{k=1}^{m'}u_kv_k=\mathsf{out}.\tag{10} \]若\(P_i\)诚实地执行所有AND门, 则意味着公式\((10)\)成立, 因此验证归结为检查以下两个条件:
- 条件1: 公式\((10)\)是否成立?
- 条件2: \(G(X)\)是否是通过公式\((9)\)正确构造得到的?
\(P_i\)首先通过RSS分享\(G(X)\)的系数, 下面说明如何检验上述两个条件.
Step 4.2: Check Polynomial Equations
对于条件1, 注意到对\(k\in[\lambda]\), \(G(k)\)是\(G(X)\)系数的线性组合, 由于所有参与方持有\(G(X)\)系数的RSS份额, 故可本地计算\([\![b]\!]^F=[\![\sum_{k=1}^\lambda G(k)-\mathsf{out}]\!]^F\). 然后, 各方可重构\(b\)并验证\(b=_?0\).
对于条件2, 注意到两个验证者分别持有\(\vec{u}\)和\(\vec{v}\), 因此可以各自计算\(p_t(X)\)和\(q_t(X)\), 其中\(t\in[s]\). 为了检验公式\((9)\)是否成立, 各方可以从\(\mathbb{F}_p\)中选择一个随机点\(r\)代入多项式看等式是否成立. 若在\(X=r\)处等式成立, 则只要域足够大, 根据Schwartz-Zipple 引理, 公式\((9)\)有压倒性的概率成立. 因此, 在验证者得到\(G(X)\)的系数\(\vec{c}\)的RSS份额后, 由于\(G(r)\)是\(G(X)\)系数的线性组合, 因而可计算\(G(r)\)的RSS份额. 又因为验证者可以各自计算\(p_t(X)\)和\(q_t(X)\), 故可以通过揭示\(G(r)\)的份额以及\(p_t(r)\)和\(q_t(t)\)来检验如下公式\((11)\):
\[\sum_{t=1}^sp_t(r)\cdot q_t(r)=G(r).\tag{11} \]Setp 4.3: Recursive Delegation
检验条件2需要验证者通信\(\{p_t(r),q_t(r)\}_{t\in[s]}\), 并评估一个长为\(s\)的内积. 为了进一步降低通信和计算复杂度, 各方可以利用递归范式对内积的评估再次委托证明者.
具体来说, 重定义\(m':=s\), 长为\(m'\)的向量\(\vec{v}:=(p_1(r),\cdots,p_s(r))\), \(\vec{u}:=(q_1(r),\cdots,q_s(r))\)以及\(\mathsf{out}:=G(r)\). 如此, 各方可以开始新一轮的长为\(m'\)内积关系\(\sum_{k=1}^{m'}u_kv_k=\mathsf{out}\)的证明任务, 恰如第一步中的公式\((7)\).
注意到在每一轮递归中, 要证明的内积长度减少了\(\lambda\)的因子, 故在经过\(\log_\lambda m\)轮后, 长度减为1, 即只需验证1次乘法关系. 此时, 验证者可以通过分别揭示其本地数据\(p_1(r)\)和\(q_1(r)\)来直接评估乘法门, 然后检查乘法关系完成验证.
An Omitted Security Issue
上述揭示\(p_1(r)\)和\(q_1(r)\)的做法是不安全的, 因为\(p_1(r)\)和\(q_1(r)\)与两个验证者的秘密输入有关. 为了保护\(p_1(r)\)和\(q_1(r)\), 设定\(p_1(0)\)和\(q_1(0)\)为随机值作为随机掩码, 如此\(p_1(X)\)和\(q_1(X)\)为\(\lambda\)阶多项式.
完整的验证协议如下:

Optimizations: Saving Computational Cost
下面介绍如何通过素域的代数结构来提高分布式零知识证明技术[6, 7]中的计算复杂度. 上述技术开销最大的部分发生在第一轮递归中, 给定压缩参数\(\lambda\)(通常为一个小常数), 本文将内积关系的长度从\(4m\)减少到\(4m/\lambda\). 本文首先回顾分布式零知识证明结构[6, 7]的第一轮递归中的计算任务.
Computation Task of First Round of Recursion
An Overview of First Round of Recursion
在本文方案下, 需要验证\(\langle\vec{u},\vec{v}\rangle=-\frac{m}{2}\), 其中\(m\)为AND门数量, \(\vec{u},\vec{v}\)是长为\(4m\)的向量, \(P_i,P_{i+1}\)持有\(\vec{u}\), 而\(P_{i},P_{i-1}\)持有\(\vec{v}\). 为了减少内积的长度, 本文首先将\(\vec{u},\vec{v}\)分解为长为\(4m/\lambda\)的子向量\(\vec{u}=(\vec{u}_1,\cdots,\vec{u}_\lambda)\)和\(\vec{v}=(\vec{v}_1,\cdots,\vec{v}_\lambda)\), 这里下标\(\{1,\cdots,\lambda\}\)表示子向量, 而不是向量元素. 然后, 证明者\(P_i\)定义两个\((\lambda-1)\)阶向量\(\vec{p}(X),\vec{q}(X)\), 使得对所有\(i\in[\lambda]\), 有\(\vec{p}(i)=\vec{u}_i\), \(\vec{q}(i)=\vec{v}\). 接下来\(P_i\)计算一个\(2(\lambda-1)\)阶多项式\(G(X)=\langle\vec{p}(X),\vec{v}(X)\rangle\). 注意到\(\langle\vec{u},\vec{v}\rangle=\sum_{i=1}^\lambda G(i)\). 现在\(P_i\)通过RSS分享\(G(X)\)的系数给其他两方. 注意到\(P_{i+1}\)可以本地计算\(\vec{p}(X)\), 而\(P_{i-1}\)可以本地计算\(\vec{q}(X)\), 故验证任务变为检查如下两点:
- \(G(X)=\langle\vec{p}(X),\vec{q}(X)\rangle\),
- \(\sum_{i=1}^\lambda G(i)=-\frac{m}{2}\).
对于第一项, 根据Schwartz-Zippel引理, 随机选取一个点\(r\), 验证\(G(r)=\langle\vec{p}(r),\vec{q}(r)\rangle\)是否成立. 注意到这归结为验证一个长度为\(4m/\lambda\)的内积关系, 因为\(\vec{p}(r),\vec{q}(r)\)两个向量的长度为\(4m/\lambda\).
对于第二项, 所有参与方可本地计算\(\sum_{i=1}^\lambda G(i)+\frac{m}{2}\)的RSS份额, 并检验其是否为0的RSS份额.
Computation Task of First Round of the Recursion
Step 1中计算开销最大的任务为计算\(G(X)\)的系数. 直接方法是首先计算\(\vec{p}(X),\vec{q}(X)\), 然后计算\(G(X)=\langle\vec{p}(X),\vec{q}(X)\rangle\). 然而, 插值一个\((\lambda-1)\)阶多项式约需\(\lambda^2\)次乘法运算. 每个\(\vec{p}(X),\vec{q}(X)\)的计算复杂度为\(4m/\lambda\cdot\lambda^2=4m\lambda\). 总的来说, 计算\(G(X)\)将需要\(8m\lambda\)次乘法运算.
注意到一个\(2(\lambda-1)\)阶多项式可以由\(2\lambda-1\)个点完全确定, 故与其分享\(G(X)\)的系数, 不如改为分享\(\{G(i)\}_{i=1}^{2\lambda-1}\), 这足以让各方计算\(G(r)\). 对每个\(i\in[2\lambda-1]\), \(G(i)=\langle\vec{p}(i),\vec{q}(i)\rangle\). 根据多项式的性质, \(\vec{p}(i)\)可表示成\(\{\vec{p}(j)=\vec{u}_j\}_{j=1}^\lambda\)的线性组合. 类似地, \(\vec{q}(i)\)可表示成\(\{\vec{q}(j)=\vec{v}_j\}_{j=1}^\lambda\)的线性组合. 因此, \(G(i)\)可通过计算\(\{\langle\vec{p}(j_1),\vec{q}(j_2)\rangle\}_{j_1,j_2\in[\lambda]}=\{\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\}_{j_1,j_2\in[\lambda]}\)的线性组合得到, 其中\(j_1,j_2\in[\lambda]\)表示子向量的索引. 本文在这里主要的观察是计算\(\{\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\}_{j_1,j_2\in[\lambda]}\)仅需要\(4m\lambda\)次乘法运算, 计算复杂度减少了一半, 本文通过这种方法来计算\(G(X)\), 而优化也高度依赖于这个观察.
总之, 第一轮的主要任务是计算\(\{\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\}_{j_1,j_2\in[\lambda]}\).
Main Optimizations
Computing \(\{\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\}\) Using Binary Operations
计算\(\{\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\}_{j_1,j_2\in[\lambda]}\)的一种直接方式是先将AND三元组转换为\(\mathbb{F}_p\)上的子向量\(\{\vec{u}_{j_1},\vec{v}_{j_2}\}_{j\in[\lambda]}\), 然后计算这些子向量的每个内积\(\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\). 然而, 在转换期间, 对每个AND三元组, 本文将验证\(a\cdot b\oplus c\cdot d\oplus e\oplus f=0\)(每个值为单个比特)转化为验证\(\sum_{k=1}^4g_k\cdot h_k+1/2=0\)(每个值为\(\mathbb{F}_p\)上的元素). 考虑到需要处理大量的AND三元组, 巨大的存储开销将会导致巨大的运行时间开销.
本文的第一个优化是使用原始数据计算\(\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle\), 而不需要显式地将它们转化为\(\mathbb{F}_p\)上的\(\vec{u}_{j_1},\vec{v}_{j_2}\). 简单起见, 本文设定\(\lambda=4\). 下面推广到\(\lambda\)是4的倍数的情形.
假设需要验证的AND三元组表示为\(\{[\![x^{(i)}]\!]^B,[\![y^{(i)}]\!]^B,[\![z^{(i)}]\!]^B\}_{i=1}^m\). 对所有\(i\in[m]\), 需要验证
\[a^{(i)}\cdot b^{(i)}\oplus c^{(i)}\cdot d^{(i)}\oplus e^{(i)}\oplus f^{(i)}=\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+\frac{1}{2}=0.\notag \]在\(\lambda=4\)的情况下, 对\(j\in[4]\), 本文设定\(\vec{u}_j=(g_j^{(i)})_{i=1}^m\)和\(\vec{v}_j=(h_j^{(i)})_{i=1}^m\).
本文观察到\(\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle=\sum_{i=1}^mg_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\). 因为每个\(g_{j_1}^{(i)},h_{j_2}^{(i)}\)都是由\(a^{(i)},b^{(i)},\cdots,f^{(i)}\)计算得到的, 故可通过原始数据来计算每个\(g_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\). 如此, 可节省转换比特值到域元素的成本.
Batching Computation for \(g_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\)
一般而言, 一个含有64个AND三元组可使用\(\texttt{uint64}\)数据类型批量存储. 具体来说, 对于每64个AND三元组, 值\(\mathbf{a}\in\mathbb Z_{2^{64}}\)用于存储\(a^{(1)},\cdots,a^{(64)}\), 同理\(\mathbf{b},\mathbf{c},\mathbf{d},\mathbf{e},\mathbf{f}\)类似.
本文的第二个优化是使用\(\mathbf{a},\cdots,\mathbf{f}\)批量计算\(g_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\). 以\(j_1=j_2=1\)为例(其他情况类似), 此时\(g_1^{(i)}=-2a^{(i)}c^{(i)}(1-2e^{(i)})\), \(h_1^{(i)}=b^{(i)}d^{(i)}(1-2f^{(i)})\). 则
\[g_1^{(i)}\cdot h_1^{(i)}=-2a^{(i)}b^{(i)}c^{(i)}d^{(i)}+4a^{(i)}b^{(i)}c^{(i)}d^{(i)}e^{(i)}+4a^{(i)}b^{(i)}c^{(i)}d^{(i)}f^{(i)}-8a^{(i)}b^{(i)}c^{(i)}d^{(i)}e^{(i)}f^{(i)}.\notag \]注意到\(\mathbf{abcd}\)可以通过首先按位AND运算, 然后将结果逐比特拆分得到. 类似地, 可先计算\(\mathbf{abcde},\mathbf{abcdf},\mathbf{abcdef}\)再逐比特拆分得到. 如此, 可加速每个\(g_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\)的计算.
Further Optimization with Carefully Chosen Coefficients
当计算\(\langle\vec{u}_{j_1},\vec{v}_{j_2}\rangle=\sum_{i=1}^mg_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\), 同时批计算\(\{g_{j_1}^{(i)}\cdot h_{j_2}^{(i)}\}_{i=1}^m\)时, 必须将结果逐比特拆分, 然后将所有比特相加.
本文的第三个优化是将一个适当的常数与每个\(m\)长内积关系相乘, 如此可以避免比特拆分. 同样以\(j_1=j_2=1\)为例, 并关注首个包含32个AND三元组的情况, 此时需要计算\(\sum_{i=1}^{32}g_1^{(i)}\cdot h_1^{(i)}\), 这要求计算\(\sum_{i=1}^{32}a^{(i)}b^{(i)}c^{(i)}d^{(i)}\), 则在计算\(\mathbf{abcd}\)之后, 还需要计算\(\mathbf{abcd}\)的最后32比特之和.
本文观察到, 若计算目标变为\(\sum_{i=1}^{32}2^{i-1}a^{(i)}b^{(i)}c^{(i)}d^{(i)}\), 则只需取最后32比特作为结果. 根据这一设想, 检验需从\(\sum_{i=1}^m(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2)=0\), 变为检验
\[\sum_{i=1}^m2^{(i-1)\bmod32}(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2)=0.\notag \]此外, 还需要保证累积误差以域大小\(p\)为界, 使得若存在某个\(i\), \(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2\neq 0\bmod p\), 则
\[\sum_{i=1}^m2^{(i-1)\bmod32}(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2)\neq0\bmod p.\notag \]因为\(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2\)的结果要么为0, 要么为1, 故有
\[\sum_{i=1}^m2^{(i-1)\bmod32}(\sum_{k=1}^4g_k^{(i)}\cdot h_k^{(i)}+1/2)\leq\sum_{i=1}^m2^{(i-1)\bmod32}<2^{27}m.\notag \]在本文中, 取\(p=2^{61}-1\), 足以验证\(2^{33}\)个AND门.
Other Optimizations
Using Mersenne Fields for Fast Arithmetic Computation
本文中将\(p\)取为梅森素数\(2^{61}-1\). 在\(\mathbb F_p\)上进行算术运算的主要瓶颈是模运算. 使用梅森素数可以通过移位和加法来加速模运算.
本文测试了\(\mathbb{F}_{2^{64}}\)和61比特梅森素数域\(\mathbb{F}_p\)上算术运算的运行时间, 主要测试两种运算: 乘法运算和内积运算, 均通过单线程测试. 结果如下表5. 可以看到, \(\mathbb{F}_p\)上的乘法运算比\(\mathbb{F}_{2^{64}}\)快7.6倍.
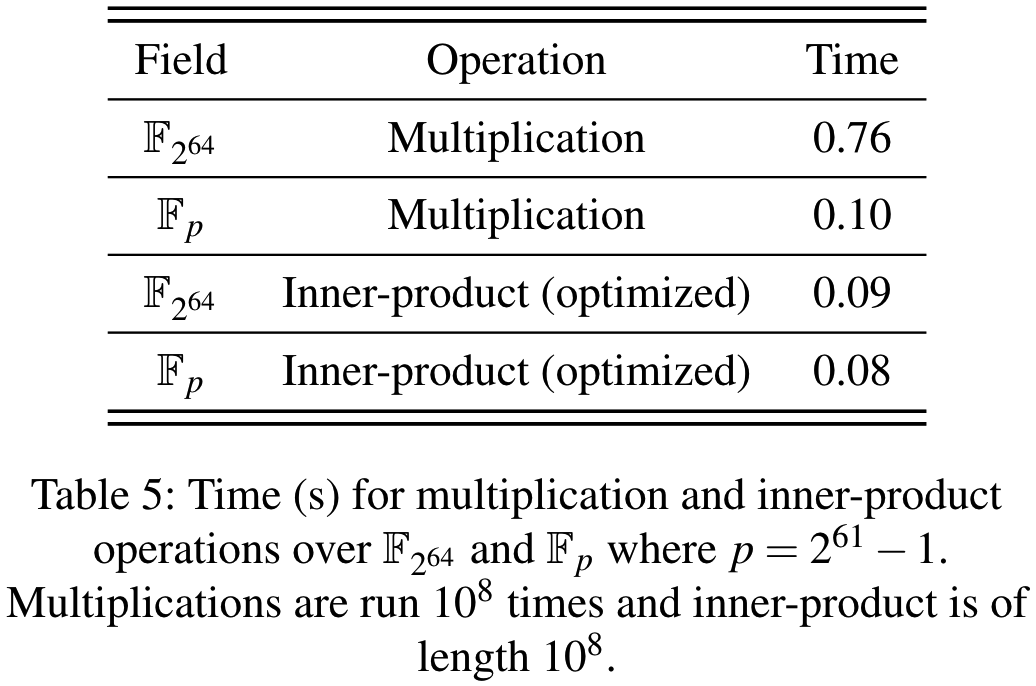
Speeding Up Inner-product Operations
分布式零知识证明[6, 7]需要在本地做很多内积运算, 为了加速内积运算, 可以先计算整数结果, 然后在最后进行一次模运算. 当需要计算多个值的加法时, 类似的技巧同样适用. 此外, 这种技巧也适用于\(\mathbb{F}_{2^{64}}\)上的点积运算, 这是因为\(\mathbb{F}_{2^{64}}\)上的乘法运算对应于将两个63阶多项式相乘, 然后对一个64阶不可约多项式进行模运算. 对于内积运算来说, 只在最后应用模运算就足够了.
Lookup Table for Computing \(\vec{p}(r),\vec{q}(r)\)
在重新解决\(G(X)\)系数的计算问题后, 计算的瓶颈变为计算\(\vec{p}(r),\vec{q}(r)\). 由于\(\vec{p}(X),\vec{q}(X)\)都是\((\lambda-1)\)阶多项式, 且向量长度为\(4m/\lambda\). 简单起见, 取\(\lambda=4\)为例(同样的方法可推广到\(\lambda\)是4的倍数的情况), 此时, \(\vec{p}(X),\vec{q}(X)\)的长度为\(4m/\lambda=m\).
令\(\vec{p}(X)=(p_1(X),\cdots,p_m(X))\), 则目标是对所有的\(i\in[m]\), 计算\(p_i(r)\). 对于每个\(p_i(r)\), 可表示为\(\{p_i(k)\}_{k=1}^4=\{g_k^{(i)}\}_{k=1}^4\)的一个固定线性组合. 本文注意到\(\{g_k^{(i)}\}_{k=1}^4\)是由\(\{a^{(i)},c^{(i)},e^{(i)}\}\)确定的, 故存在一个映射\(M:\{0,1\}^3\rightarrow\mathbb{F}_p\), 使得对于所有\(i\in[m]\), 都有\(M(a^{(i)},b^{(i)},c^{(i)})=p_i(r)\). 因此, 本文为\(M\)建立了一个大小为\(2^3=8\)的查找表(Lookup Table), 并通过输入\(a^{(i)},b^{(i)},c^{(i)}\)查表进行检验.
一般而言, 当\(\lambda=4\)时, 表的大小为\(2^{3\lambda/4}\). 本文实验中, 在递归的第一轮取\(\lambda=32\), 这是为了最大限度地利用上述优化带来的第一轮快速计算优势. 此时, 表的大小为\(2^{24}\). 为了减小表的大小, 本文构造了两个表, 其中一个用于\(\{p_i(k)\}_{k=1}^{16}\), 另一个用于\(\{p_i(k)\}_{k=17}^{32}\). 在这种方法下, 每个表的大小为\(2^{12}\), \(p_i(r)\)可以从两个表的结果加和得到.
Parameter Setup
与在协议最后检验所有AND三元组不同, 本文将AND三元组分成不同的批次, 并对每个批次并行应用本文的验证协议. 本文注意到批处理大小对运行时间影响很小, 选取批处理大小为\(\texttt{bs}=640000\)来达到协议的最佳运行时间.
由于第一轮计算得到了显著的改进, 本文的协议在第一轮使用压缩参数\(\lambda=32\), 其余轮使用\(\lambda'=8\). 在这种情况下, 本文协议能达到的可靠性误差为
\[\frac{2\lambda}{p-\lambda}+\frac{2\lambda'(\log_{\lambda'}(\texttt{bs}/\lambda)+1)+1}{p-\lambda'-1}\leq2^{-53},\notag \]对大多数应用来说已经足够.
Application: Secure DNN Inference
支持截断和比较等非线性运算的通用方案是基于二进制计算设计特定的协议, 对隐私保护机器学习(PPML)来说至关重要. 本文的协议可作为一个高效的原语来优化这一部分, 下文中本文将说明为什么在当前最先进的情况下, 非线性运算如此昂贵的原因, 本文仅关注诚实大多数三方计算的设置.
Fixed-Point Arithmetic
定点算术的思想是在有限域/环上模拟实数运算. 在定点表示中, 一个\(k\)比特的有符号定点数\(\tilde{x}\)由两部分组成: \(e\)比特的整数部分和\(d\)比特的小数部分, 满足\(k=e+d\). 可通过设定\(x:=2^d\cdot\tilde{x}\)将\(\tilde{x}\)映射为环\(\mathbb Z_{2^k}\)上的元素\(x\).
定点数的加法和乘法可以映射到环元素上的加法和乘法运算. 但是, 两个定点数的乘法的小数部分长度将翻倍. 为了继续计算, 乘法结果需要对小数部分进行适当的调整, 截断最后\(d\)比特, 使得小数部分保留\(d\)比特.
Comparison
比较是机器学习中的一个基本原语. 神经网络中的激活函数ReLU和最大池化层都可以分解为比较运算. 正如下面将要讨论的, 精确截断协议也需要安全的比较.
一个环\(\mathbb Z_{2^k}\)上的比较协议取份额\([\![x]\!]^R\)和\([\![y]\!]^R\)为输入, 输出\([\![z]\!]^R\), 其中当\(x\geq y\)时, \(z=0\), 否则\(z=1\). 文献中通常将安全比较问题转化为MSB提取问题. 首先, 将秘密份额从\(\mathbb{Z}_{2^k}\)转化到\(\mathbb Z_2\), 然后各方安全计算特定的二进制电路(如全加器或并行前缀加法器等)来提取两个秘密之差. 在目前最先进的解决方案SWIFT和ABY3中, \(\mathbb{Z}_{2^k}\)上两个元素的安全比较需要计算一个有\(3k\)个AND门的二进制电路.
Truncation
环上的截断协议输入整数\(x\in\mathbb{Z}_{2^k}\)的份额\([\![x]\!]^R\), 并输出\(x'\)的份额, 其中\(x'=[x/2^d]\).
在机器学习的安全计算协议中, 截断运算在每次算术乘法或算术点积后被调用, 应用广泛. 截断协议的设计有两种趋势: 达到精确截断(Exact Truncation)或者具有1比特误差的概率截断(Probabilistic Truncation).
Exact Truncation: 精确截断协议总是精确计算\(x'=\lfloor x/2^d\rfloor\). 实现精确截断需要计算比较.
Probabilistic Truncation: 概率截断协议计算\(x'=\lfloor x/2^d\rfloor+w\), 其中\(w=1\)的概率为\(\gamma:=\frac{x\bmod 2^d}{2^d}\), \(w=0\)的概率为\(1-\gamma\). 这里\(\gamma\)是\(x/2^d\)的小数部分到0的距离.
虽然概率截断的出发点是为了避免精确截断所需的安全比较, 但本文注意到, 已知的基于[11]的高效概率截断协议并不能安全地计算出所需的功能, 因而不得不使用昂贵的精确截断, 如此大大增加了AND门的数量. 在下表1中, 本文使用MP-SPDZ分别编译了具有/不具有概率截断的三个神经网络, 统计两种情况下使用概率截断和精确截断时所需的二进制AND门数量, 可见精确截断比概率截断需要更多的AND门.
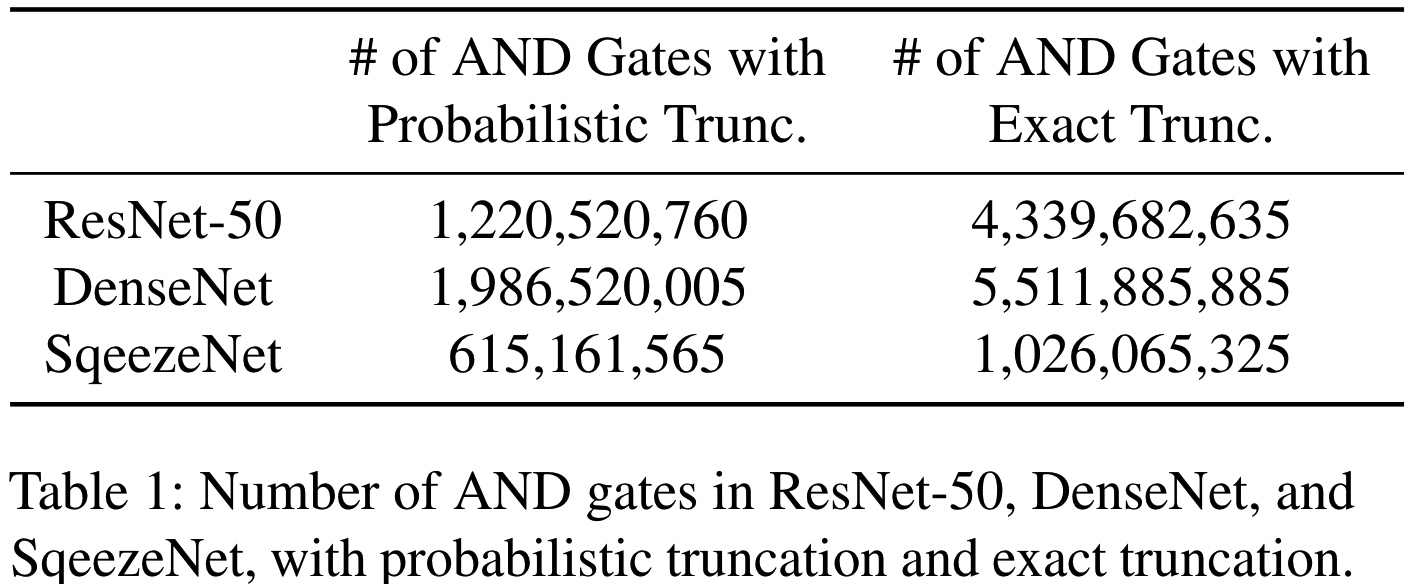
On the Security Issue of Probabilistic Truncation Protocols
Overview of the Approach in [11]
下面给出Catrina和Hoogh所提方案的概述. 考虑\(\mathbb Z_{2^k}\)上的一般线性秘密共享方案\(\Sigma\), 令\([x]\)表示\(x\)的\(\Sigma\)份额. 设起始时所有参与方持有\(x\)的秘密份额\([x]\), 并进一步假设\(x<2^{k-\tau}\), 其中\(\tau\)是安全参数. 假定目标是截断\(x\)的最后\(d\)比特的结果\(x^d\)的份额\([x^d]\), 则在\(\mathcal{F}_\mathrm{truncPair}\)混合模型下[11]的方法可总结为如下协议1, 其中\(\mathcal{F}_\mathrm{truncPair}\)选取一个随机\(r\), 生成\(([r],[r^d])\)并分发给所有参与方.

令\(x_d\)表示\(x\)的最后\(d\)比特. 当\(x+r<2^k\), 且以\(x/2^k<2^{-\tau}\)的概率发生时, 上述协议的结果份额与其发生概率\(p\)满足:
\[x'= \begin{cases} x^d+1,& p=\dfrac{x_d}{2^d},\\ x^d,& p=1-\dfrac{x_d}{2^d}. \end{cases}\notag \]原因: 当\(x+r<2^k\)时,
- 若\(x_d+r_d<2^d\), 则\(x+r=x_d+r_d+2^d(x^d+r^d)\). 故\((x+r)^d=x^d+r^d\), 且\(x'=(x+r)^d-r^d=x^d\);
- 若\(x_d+r_d\geq2^d\), 则\(x+r=(x_d+r_d-2^d)+2^d(x^d+r^d+1)\). 故\((x+r)^d=x^d+r^d+1\), 且\(x'=(x+r)^d-r^d=x^d+1\).
乍看之下, \(P_1\)恢复的值为\(x+r\), 被随机值\(r\)所盲化, 因此\(P_1\)不知道\(x\)的任何信息. 然而, 对于一个固定的输入\([x]\), 输出\(x'\)是向上取整还是向下取整完全取决于协议中唯一引入的随机数\(r\). 这是意味着在基于模拟安全性证明中给定\(P_1\)的视图, \(x'\)是固定的. 另一方面, 对于半诚实安全性来说, 预期\(x'\)被一个理想功能所截断, 这个功能应独立于\(P_1\)的视图.
Security Issue
为了证明[11]中方法的安全性问题, 首先需要为其定义理想功能, 考虑如下理想功能\(\mathcal{F}_\mathrm{truncPr}\).

定理2: 设\(\Sigma\)是\(\mathbb{Z}_{2^k}\)上的线性秘密共享方案, 满足任意\(t\)个份额不能得到秘密的任何信息. 令\(\tau\)是安全参数. 对所有\(\varepsilon=\texttt{negl}(\tau)\), 协议TruncPR对于具有统计误差\(\varepsilon\)的\(\mathcal{F}_\mathrm{truncPr}\)不是\(t\)-隐私的.
证明: 反证法, 假设TruncPR对\(\mathcal F_\mathrm{truncPr}\)是\(t\)-隐私的. 根据定义, 存在一个理想敌手\(\mathcal S\), 使得对所有满足\(x<2^{k-\tau}\)的输入份额\([x]\), 都有
\[([\tilde{x}'],\texttt{View}_\mathcal C([x]))\approx_\varepsilon([x'],\mathcal S(\mathcal C,[x]_\mathcal C,[x']_\mathcal{C})),\notag \]其中\([\tilde{x}']\)表示在现实世界中的输出份额, \([x']\)表示在理想世界中的输出份额, \([x']_\mathcal C\)表示腐化方持有的\([x']\)的份额. 这可以推知
\[(\tilde{x}',\texttt{View}_\mathcal C([x]))\approx_\varepsilon(x',\mathcal S(\mathcal{C},[x]_\mathcal C,[x']_\mathcal C)).\tag{12} \]考虑\(x=2^{d-1}\), \(P_1\)被腐化的情况. 首先断言在理想世界中, \(\tilde{x}'\)由\(\texttt{View}_\mathcal C([x])\)确定. 注意到在现实世界中, \(\tilde{x}'=(x+r)^d-r^d\). 因此\(\tilde{x}'\)由\(x\)和\(r\)确定. 由于输入\([x]\)是固定的, 且腐化方\(P_1\)能得到\(x+r\), 故给定腐化方的视图, \(\tilde{x}'\)是固定的. 总之, 对于\((\tilde{x}',\texttt{View}_\mathcal C([x]))\)的分布, 给定\(\texttt{View}_\mathcal C([x])\), \(x'\)是固定的.
下面分析\((x',\mathcal S(\mathcal{C},[x]_\mathcal C,[x']_\mathcal C))\)的分布. 因为\(\Sigma\)是\(\mathbb{Z}_{2^k}\)上的线性秘密共享方案, 满足任意\(t\)个份额不能得到秘密的任何信息, 故腐化方持有的\([x']\)份额与秘密\(x'\)相互独立. 由于\(x=2^{d-1}\), \(\mathcal F_\mathrm{truncPr}\)将以\(1/2\)的概率设定\(x'=x^d=0\)或者\(x'=x^d+1=1\). 而用于确定\(x'\)的随机性与腐化方持有的\([x]\)和\([x']\)的份额无关, 因此给定\(\mathcal S(\mathcal{C},[x]_\mathcal C,[x']_\mathcal C)\), \(x'\)是一个随机比特. 总之, 对于分布\((x',\mathcal S(\mathcal{C},[x]_\mathcal C,[x']_\mathcal C))\), 给定\(\mathcal S(\mathcal{C},[x]_\mathcal C,[x']_\mathcal C)\), \(x'\)是一个随机比特.
这意味着公式\((12)\)不成立, 故不存在这样的理想敌手\(\mathcal S\). 即协议TruncPR对\(\mathcal F_\mathrm{truncPr}\)不是\(t\)-隐私的. 证毕.
Evaluation
本节展示本文协议的实现及其在DNN推理中的应用, 以及与之前最好的工作进行比较的基准结果. 本文的实现基于MP-SPDZ, 开源地址: malicious_3pc_binary.
下文中, BGIN19指文献[7]的在\(\mathbb{F}_{2^{64}}\)上基于FLIOP的验证方案, FLNW17指文献[21]基于cut-and-choose的方案, Semi指文献[3]的半诚实安全方案, SW指文献[1]基于RSS的最先进的恶意安全三方计算协议SpdzWise.
Benchmarks for Binary Circuits
Binary Circuits with Different Depths
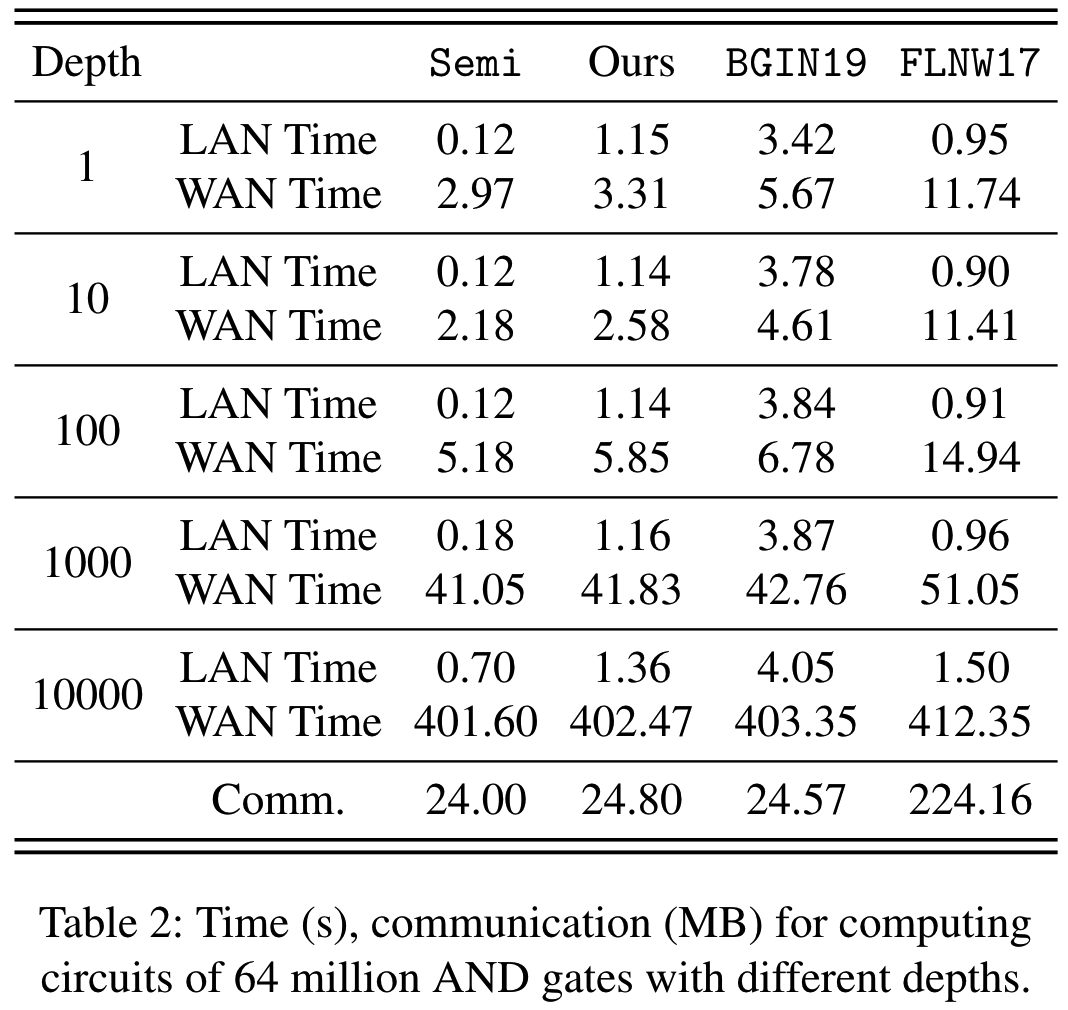
构造1~10000个不同深度的纯二进制电路, 每个电路在随机输入下计算6400万个AND门, 则不同方案的协议运行时间和全局通信开销如下表2. 在LAN下的运行时间上, 本文协议比BGIN19快3~3.4倍, 比FLNW17慢1~1.3倍. 在WAN下, 本文协议比BGIN19快1~1.8倍. 这里的差距比LAN下小, 因为在WAN环境下, 通信复杂度成为主要瓶颈, 而本文协议与BGIN19的通信复杂度非常接近. 由于节省了通信复杂度, 本文协议比FLNW17在1~100的深度下快2.6~4.2倍. 对于深度为1000~10000的电路, 由于网络延迟成本占主导地位, 所有协议的性能都很接近.
AES Circuit
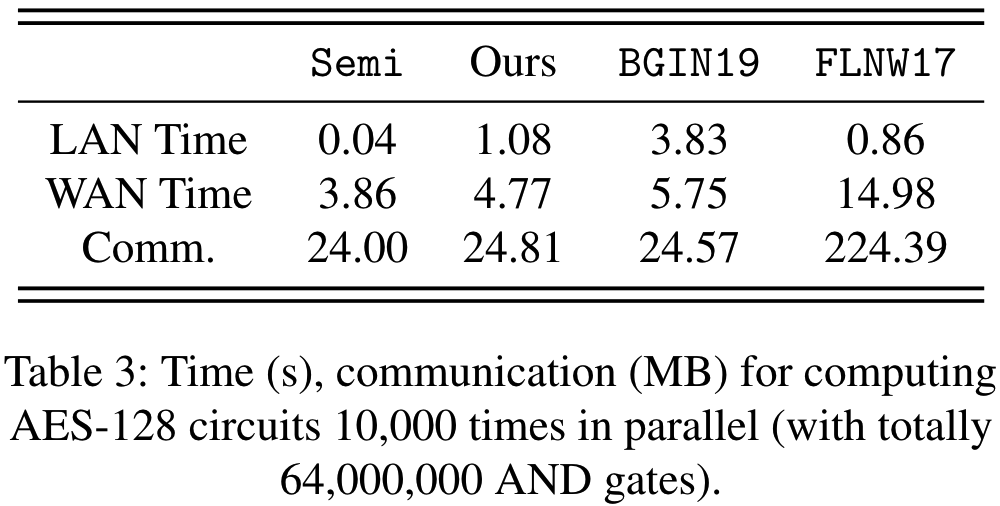
本文并行MP-SPDZ提供的AES-128电路10000次以测试效率, 其中每个AES-128电路包含6400个AND门, 28176个XOR门和2087个INV门, 深度为60. 测试结果如下表3. 可以看到, 在LAN设定下, 本文的协议比BGIN19快3.5倍, 比FLNW17慢1.25倍. 在WAN设定下, 本文的协议比BGIN快1.2倍, 比FLNW17快3.1倍. 总体来看, 本文协议在LAN下比BGIN19快3倍, 且接近FLNW17, 在通信开销上比FLNW17节省了9倍.
Maliciously Secure DNN Inference
本文运行了三个业界常用的深度神经网络: ResNet-50, DenseNet, SqeezeNet. 考虑不同安全模型的比较, 结果如下表4.
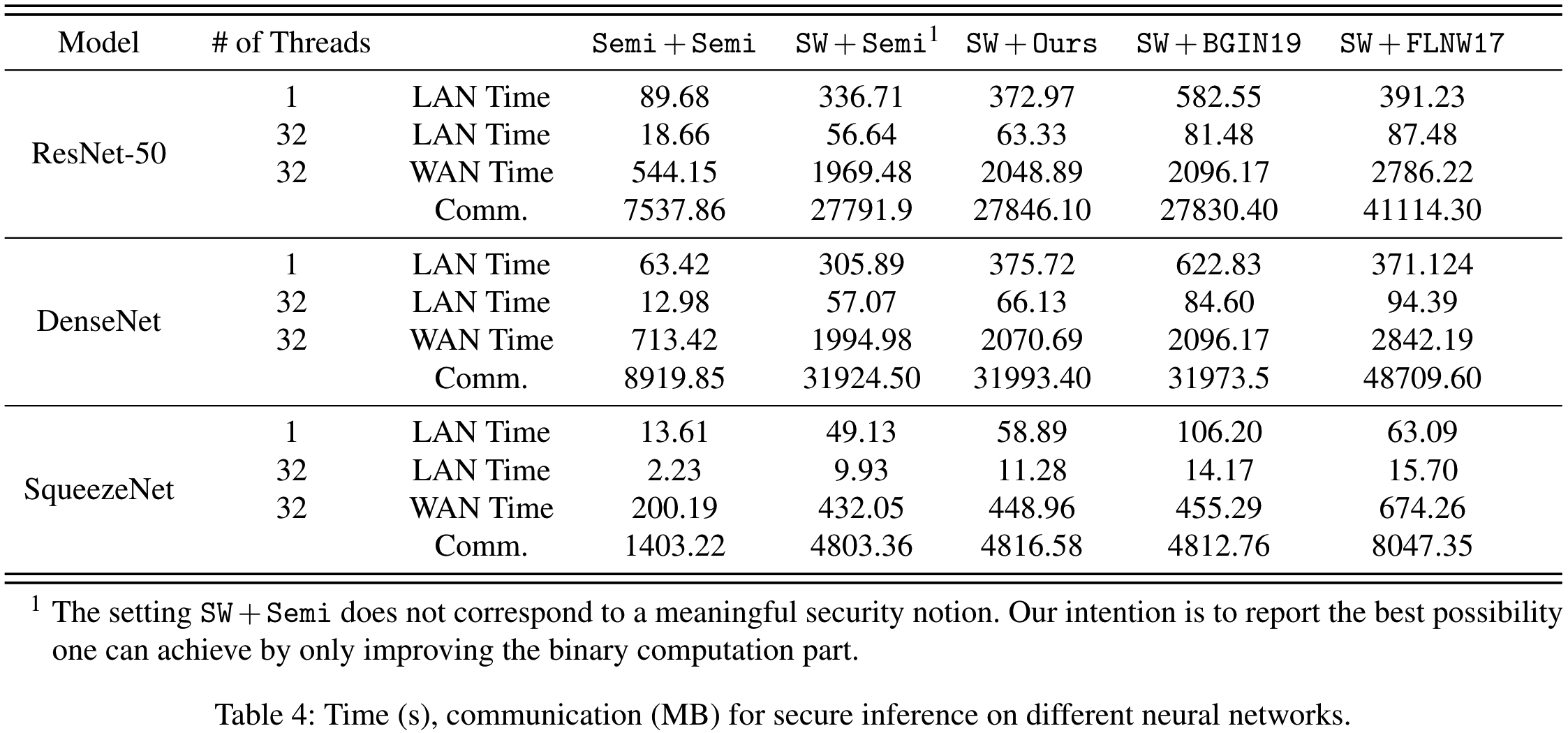
对于总通信量来说, SW+Ours和SW+BGIN19与基准SW+Semi相近. 另一方面, 与SW+Ours和SW+BGIN19相比之下, SW+FLNW17需要多1.5~1.7倍的通信开销. SW+FLNW17的额外通信开销是由于二进制部分的协议FLNW17造成的.
在LAN设定下, SW+Ours比SW+BGIN19快1.3~1.8倍, 比SW+FLNW17快1~1.4倍. 在WAN设定下, SW+Ours几乎与SW+BGIN19一样快, 同时比SW+FLNW17快1.4~1.5倍.
对于通信复杂度, SW+Ours和SW+BGIN19实现恶意安全的开销为完全半诚实协议的3.4~3.7倍, SW+FLNW17则为6.1~6.5倍. 与SW+Semi的对比来看, 可以看到SW+Ours和SW+BGIN19的主要额外通信成本来自于对DNN推理中二进制部分以外的计算实现恶意安全, 这部分计算包括使用SW进行算术运算, 使用dabits技术进行算术份额与二进制份额之间的转换等等. 另一方面, 对于SW+FLNW17, 由于使用FLNW17进行二进制运算, 额外的成本也来源于二进制部分.
对于运行时间, 与完全半诚实协议相比, 在LAN设定下SW+Ours慢3.4~5.9倍, SW+BGIN19慢4.2~9.8倍, SW+FLNW17慢3.7~6.2倍. 在WAN设定下, 差距缩小, SW+Ours慢2.2~3.8倍, SW+BGIN19慢2.3~3.9倍, SW+FLNW17慢4.2~5.4倍.
Conclusion
本文面向诚实大多数的二进制电路提出了具有恶意安全的三方计算协议. 本文使用的分布式零知识证明来验证在\(\mathbb F_2\)进行的半诚实计算. 但不同的是, 本文将\(\mathbb{F}_2\)上的半诚实计算的验证转化为\(\mathbb{F}_p\)上的计算, 并利用素域的代数结构来加速计算. 因此可实现比[7]更低的计算开销, 以及亚线性级别的额外通信开销.
References
[1] Mark Abspoel, Anders Dalskov, Daniel Escudero, and Ariel Nof. An efficient passive-to-active compiler for honest-majority mpc over rings. In International Conference on Applied Cryptography and Network Security, pages 122–152. Springer, 2021.
[2] Toshinori Araki, Assi Barak, Jun Furukawa, Tamar Lichter, Yehuda Lindell, Ariel Nof, Kazuma Ohara, Adi Watzman, and Or Weinstein. Optimized honest-majority mpc for malicious adversaries — breaking the 1 billiongate per second barrier. In 2017 IEEE Symposium on Security and Privacy (SP), pages 843–862, 2017.
[3] Toshinori Araki, Jun Furukawa, Yehuda Lindell, Ariel Nof, and Kazuma Ohara. High-throughput semi-honest secure three-party computation with an honest majority. In Edgar R. Weippl, Stefan Katzenbeisser, Christopher Kruegel, Andrew C. Myers, and Shai Halevi, editors, Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, October 24-28, 2016, pages 805–817. ACM, 2016.
[4] Donald Beaver. Efficient multiparty protocols using circuit randomization. In Annual International Cryptology Conference, pages 420–432. Springer, 1991.
[6] Dan Boneh, Elette Boyle, Henry Corrigan-Gibbs, Niv Gilboa, and Yuval Ishai. Zero-knowledge proofs on secret-shared data via fully linear pcps. In Annual International Cryptology Conference, pages 67–97. Springer, 2019.
[7] Elette Boyle, Niv Gilboa, Yuval Ishai, and Ariel Nof. Practical fully secure three-party computation via sublinear distributed zero-knowledge proofs. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, pages 869–886, 2019.
[11] Octavian Catrina and Sebastiaan de Hoogh. Improved primitives for secure multiparty integer computation. In International Conference on Security and Cryptography for Networks, pages 182–199. Springer, 2010.
[13] David Chaum. Blind signature system. In Advances in cryptology, pages 153–153. Springer, 1984.
[21] Jun Furukawa, Yehuda Lindell, Ariel Nof, and Or Weinstein. High-throughput secure three-party computation for malicious adversaries and an honest majority. In Annual international conference on the theory and applications of cryptographic techniques, pages 225–255. Springer, 2017.
本文标题: Efficient 3PC for Binary Circuits with Application to Maliciously-Secure DNN Inference
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16877849945247.html
本站文章采用 知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间: 2023-06-26T21:09:54+08:00