云中雨雾

    Towards Practical Secure Neural Network Inference: The Journey So Far and the Road Ahead

    2022/11/04 09:13 上午 标签: #隐私保护机器学习

    最近在eprint上看到一篇关于神经网络安全推理的非常不错的综述性文章Towards Practical Secure Neural Network Inference: The Journey So Far and the Road Ahead, 概述了迄今为止面向安全推理提出的主要方法、不同方法之间的特性以及所使用的技术. 最后还总结了大规模部署时所面临的挑战. 这里只摘录了其中的一些要点和案例与大家分享, 更多的内容请查看原文.

    1. 简介

    神经网络(Neural Networks, NN)包含两个主要阶段: 训练阶段和推理阶段. 这两个阶段所进行的运算是类似的, 主要不同是训练需要通过反向传播来调整神经网络不同层中的权重参数, 而后者权重已经给出, 此外, 当考虑安全性和隐私性时, 两者要求也不相同, 对于推理阶段来说, 主要考虑如下两个要点:

    1. 低时延(low latency): 推理应是快速的.
    2. 高准确性(high accuracy): 推理结果应尽可能是正确的.

    推理常见于MLaaS服务场景中, 模型提供商(Server)负责提供已经训练好的NN模型\(f\)作为服务提供给客户(Client), 客户持有输入\(x\), 希望得到\(f(x)\), 但是客户希望\(x\)是保密的, 而模型提供商也不希望与客户共享NN模型\(f\)的信息. 安全神经网络推理(secure neural networks inference, SNNI)问题即是在满足这些安全需求的同时计算\(f(x)\). 有些文献也把安全推理称为隐私保护推理(privacy-preserving inference), 不经意预测(oblivious prediction).

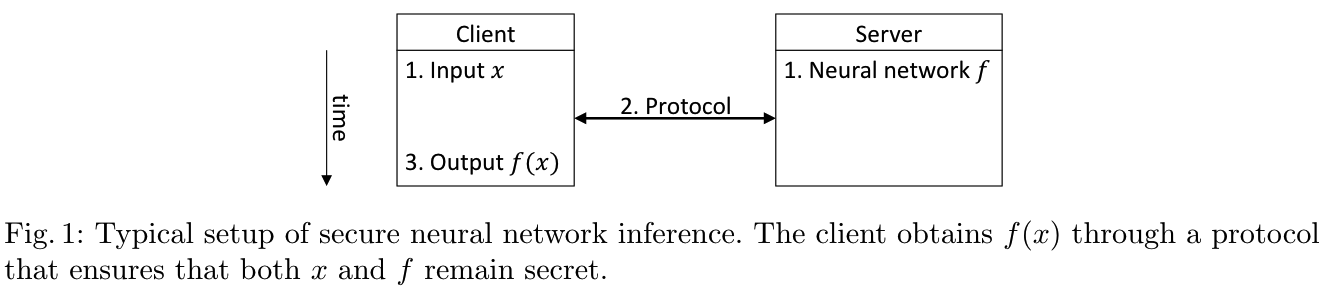
    image-20221031092831892

    目前安全推理已有的解决方案有两种:

    • 基于密码学技术: 同态加密(HE)、安全多方计算(MPC)
    • 基于可信硬件: 可信执行环境(TEE)

    这些方法通常需要在高效性、安全性、准确性和可用性等方面进行权衡.

    传统意义上的神经网络是由神经元组成的, 一个神经元包含一系列权重(weight)\(w_1,\cdots,w_n\in\mathbb R\)和偏置项(bias)\(b\in\mathbb R\), 神经元首先计算\(y=\sum_{i=1}^nw_ix_i+b\), 然后将\(y\)作为非线性激活函数\(f:\mathbb R\rightarrow\mathbb{R}\)来计算输出\(z=f(y)\).

    image-20221031100013634

    NN由一系列层组成, 第一层称为输入层, 最后一层称为输出层, 其余层被称为隐藏层, 隐藏层通常由神经元组成, 第\(i\)层的输出是第\(i+1\)层的输入. 现代NN中不再局限于单个神经元, 而是使用了许多不同类型的层, 例如:

    • 全联接层(Fully-connected layer, FC): 包含权重矩阵. 通过计算输入向量与权重矩阵的乘积来计算输出向量.
    • 卷积层(Convolutional layer, Conv): 包含一组比输入小的特征图(feature map)的权重矩阵, 通过在输入上移动特征图大小的窗口(sliding window)来计算特征图与滑动窗口中输入部分的点积来计算输出结果. 卷积层是卷积神经网络(CNN)中非常重要的组成部分, CNN广泛应用于图像处理任务.
    • 激活层(Activation layer): 将\(\mathbb{R}\rightarrow\mathbb{R}\)的激活函数应用于输入的每个元素, 以此计算输出. 根据函数不同, 可分为ReLU激活层、tanh激活层等.
    • 池化层(Pooling layer): 通过在输入上滑动大小为\(k\)的窗口并应用\(\mathbb{R}^k\rightarrow\mathbb{R}\)池化函数来计算输出结果. 最常见的池化函数是最大值函数, 对应于最大池化层(Max-Pool layer).

    FC层和Conv层称为线性层, 因为输出是其输入的线性函数, Conv层可以用矩阵乘法来表示. 而其他大多数层都是非线性层.

    神经网络架构通常包含层的数量、类型和大小等信息, 以下是Chameleon中给出的一个CNN架构的例子.

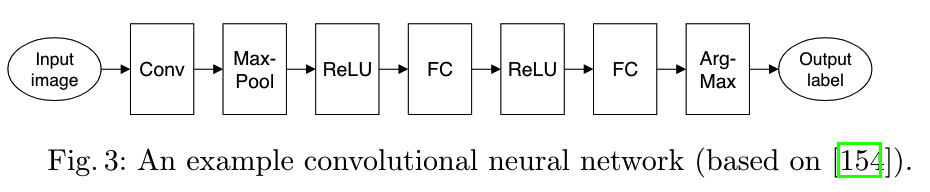
    image-20221031134237622

    2. 安全推理方案的特征

    下表中给出了现有SNNI方案的特征.

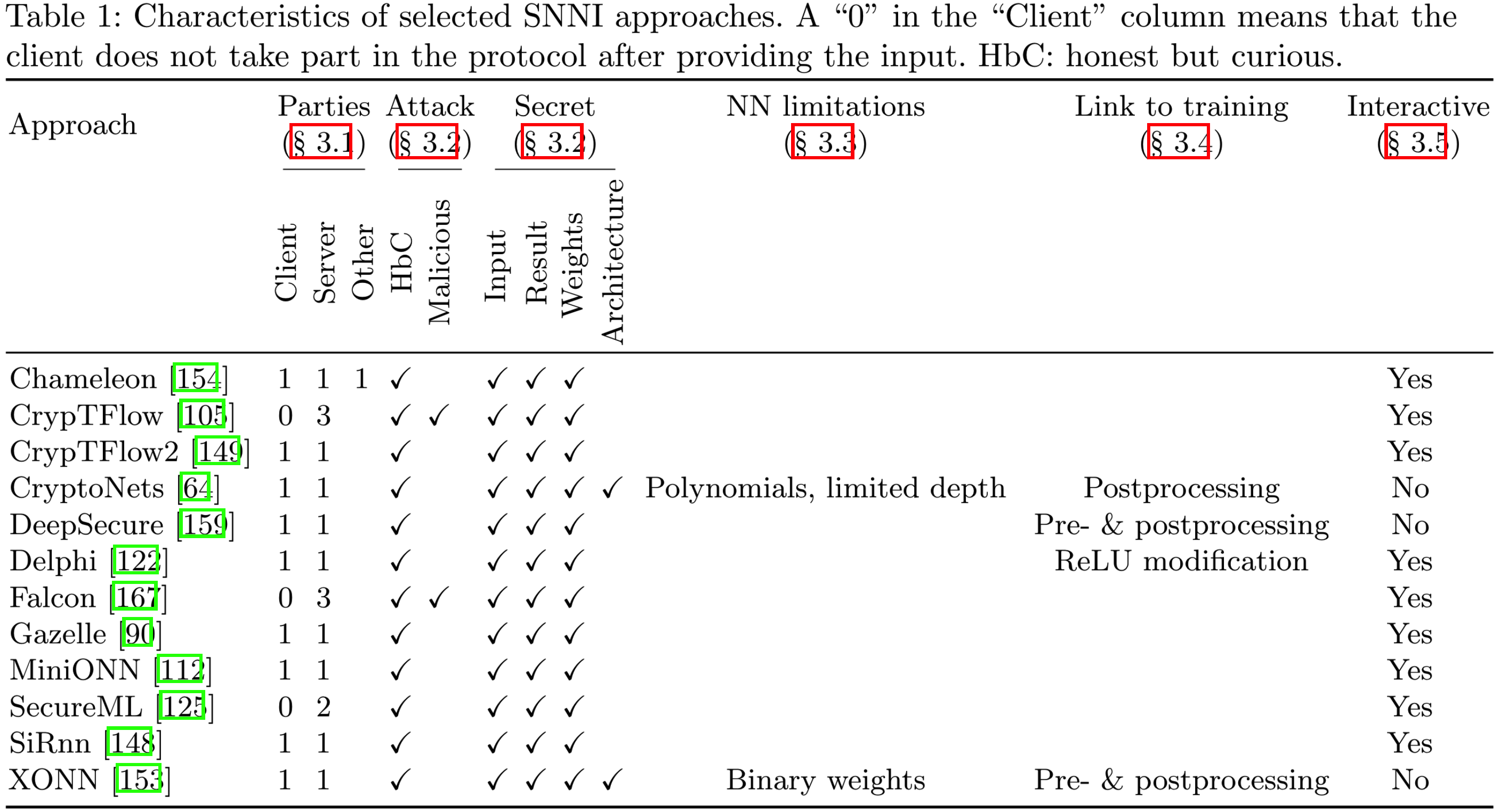
    image-20221031142037663

    2.1 参与方数量与角色

    通常SNNI是个两方计算问题, 即Client持有输入, Server持有神经网络. 但还有三方、甚至四方等更多参与方设定下的方案, 此时不共谋假设是确保协议安全性中非常重要的一环. 这些参与方设定可总结如下:

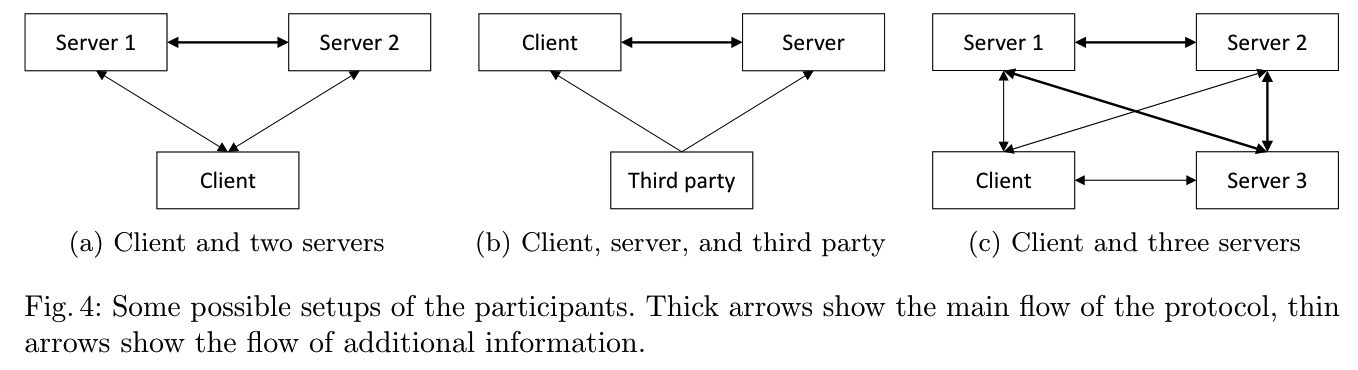
    image-20221031142727497

    • (a) 2个不共谋的Servers, 例如: SecureML
    • (b) 1个Server, 但引入不涉及输入的第三方(如TEE)生成必要的随机性加速推理, 例如: Chameleon
    • (c) 3个不共谋的Servers, 例如: ABY3, Falcon, ASTRA, BLAZE, SecureNN, SWIFT
    • (d) 4个不共谋的Servers, 这些方案认为协议上的效率提升有利于减少部署成本, 例如FALSH, Trident, Tetrad

    2.2 安全属性

    2.2.1 敌手模型

    • Semi-honest model: 敌手不会破坏协议, 在SNNI问题中更常见.
    • Malicious model: 敌手可能发送错误消息从而破坏协议, 研究较少. 例如:
      • CrypTFlow的Aramis组件: 依赖于具有完整性保证的可信硬件实现(Intel SGX), 为消息签名来验证是否遵守协议, 由此产生的额外开销大约是Semi-honest模型的\(3\times\);
      • ABY3、XONN都可实现恶意安全, 但没有提供性能评估.
      • Falcon实现了具有中止安全性的恶意安全, 当发现恶意行为时, 协议中止(Security with abort).
      • FALSH、SWIFT、Trident和Tetrad对至多存在1个腐化方的情况下实现了恶意安全, 同时还达到了公平性(Fairness)和输出可达性(Robustness/Guaranteed output delivery, GOD).

    此外还有一些方法假设Client是恶意的情况, 例如MUSE.

    2.2.2 保密目标

    根据应用场景的不同, 不同类型信息的保密性非常重要, 典型的保密目标如下:

    1. Client的秘密输入.
    2. Client得到的推理结果.
    3. Server的神经网络权重和偏置项.
    4. Server的神经网络架构(层数、层的类型、层的大小等).

    SNNI方案通常只考虑1-3, 而4通常不考虑, 只在通信模式中才考虑.

    2.2.3 黑盒攻击

    如果能实现上述保密目标, 则Client无法获知除了推理结果之外的其他信息. 但通过足够数量的查询推理, 推理结果仍可能泄漏NN的某些信息. 这涉及如下几种攻击:

    • 模型提取攻击(model extraction attack): Client尝试提取模型的参数.
    • 模型反演攻击(model inversion attack): 确定给定标签的原型样本.
    • 成员推理攻击(membership inference attack): 找出给定的输入是否出现在训练集中.

    这些是MLaaS的固有属性, 与确保推理过程安全的特定技术无关. 通常可以限制Client进行的查询数或限制Client从推理中获取的信息来避免这些攻击. 但是大部分SNNI方案不考虑这些攻击.

    2.3 受支持的神经网络

    目前暂不清楚有效支持所有类型NN的安全计算的通用技术. SNNI的多数工作都集中在开发适用于某种神经网络类型的特定技术, 要么受限于所支持的层类型, 有么受限于权重的范围.

    2.3.1 受支持的层类型

    理想的SNNI方案应支持FC层、Conv层、激活函数层、最大池化层、softmax或argmax. 常见方案支持的层类型如下:

    image-20221031160001379

    2.3.2 受支持的权重范围

    有一些SNNI方案限制了NN中处理的数据类型, 从而加快推理效率. 例如:

    • 离散化的神经网络(Discretized NN): 权重都是整数, 神经元的输入和输出都在\(\{1,-1\}\)中;
    • 二值神经网络(Binary NN): 权重和激活值都只能取\(\{1,-1\}\). 例如XONN.

    这些限制方法可以高效地实现NN中所涉及的算术运算, 但NN的准确率将降低.

    2.4 与训练的联系

    SNNI方法与训练存在很大的差异, 如下图所示,

    • (a) 涵盖了同一框架下的安全训练和安全推理, 例如: Falcon.
    • (b) 从预训练的模型开始, 完全与训练无关, 不需要对模型进行修改, 例如: CrypTFlow.
    • (c) 对预训练的模型进行转换, 使其更适合SNNI, 例如: CryptoNets.
    • (d) 对训练过程进行大幅修改从而提高效率, 例如: Delphi、XONN.

    image-20221031162036945

    尽管这些优化有助于提高效率, 但可能会影响现有机器学习模型的可用性.

    2.5 交互性

    轮复杂度(Round complexity): Client和Server通信的轮数. 大多数现有SNNI方法的通信模式有如下两种:

    • 交互式(interactive): Client和Server在评估NN的每一层后都进行通信, 交互式方案需要通信\(O(n)\)轮, 其中\(n\)为层数;
      • 优点: 可对不同类型的层选用最合适的协议, 实现更高的效率;
      • 缺点: 会泄漏NN架构信息给Client, 且要求Client全程参与, 不利于移动设备.
      • 例子: 基于秘密共享的SNNI方案、混合方案.
    • 非交互式(non-interactive): Client和Server的通信只发生在协议开始时和结束时, 非交互式方案只需通信\(O(1)\)轮.
      • 优点: NN架构信息对Client保密.
      • 例子: 基于混淆电路和同态加密的SNNI方案.

    2.6 离线预处理

    许多方法中协议的某些部分独立于Client的输入, 因此可将协议分为独立于Client输入的离线预处理阶段和依赖于输入的在线阶段. 使用这种离线/在线范式的方法有SecureML, MiniONN, Chameleon, Delphi, Falcon等等. 离线阶段的常见活动有: 生成Beaver三元组, 或者其他用于茫化秘密的关联随机数.

    离线/在线范式优缺点如下:

    • 优点: 适合Client与Server是长期关系, 但推理请求只是偶尔发生的场景, 此时系统有充足的时间进行预处理, 因此方案的优化目标在于减少在线阶段的处理时间.
    • 缺点: 不太适合新Client加入和推理请求频繁发生的场景, 此时系统没有空闲时间进行预处理, 因此方案的优化目标在于减少计算消耗的总时间.

    3. 解决方案

    3.1 同态加密(HE)

    早期将HE用于SNNI问题的工作是[1-2]. 使用HE的优点是可以满足所有保密目标, 其主要的难点则在于非线性函数的计算和全同态加密方案的选取.

    3.1.1 非线性函数的计算

    1. 使用该函数的多项式近似, 因为多项式计算只涉及FHE方案支持的乘法和加法, 尽管这仍然非常昂贵. 这里的“昂贵”指的是: 计算时间的增加、噪音的大幅增加和消息空间大小的增加.
    2. 使用简化的激活函数. 例如CryptoNets使用平方函数代替激活函数, 求和代替池化; FHE-DiNN使用符号函数作为激活函数等.

    由于HE评估非线性层很困难, 故一些方案建议仅对网络中的线性层使用HE, 而对非线性层使用其他MPC技术.

    3.1.2 同态加密方案的选取

    • 第一代FHE: Gentry所提出的方案, 噪音增长太快, 降低噪音的自举开销巨大;
    • 第二代FHE: BGV、BFV、yashe, 噪音增长变慢, 比第一代高效;
    • 第三代FHE: 改善了自举的时间;
    • 第四代FHE: CKKS方案, 可用于浮点数运算, 适合NN. 使用FHE解决SNNI问题的方案有: CryptoNets, LoLa, SHE等. 这些方案对比如下:

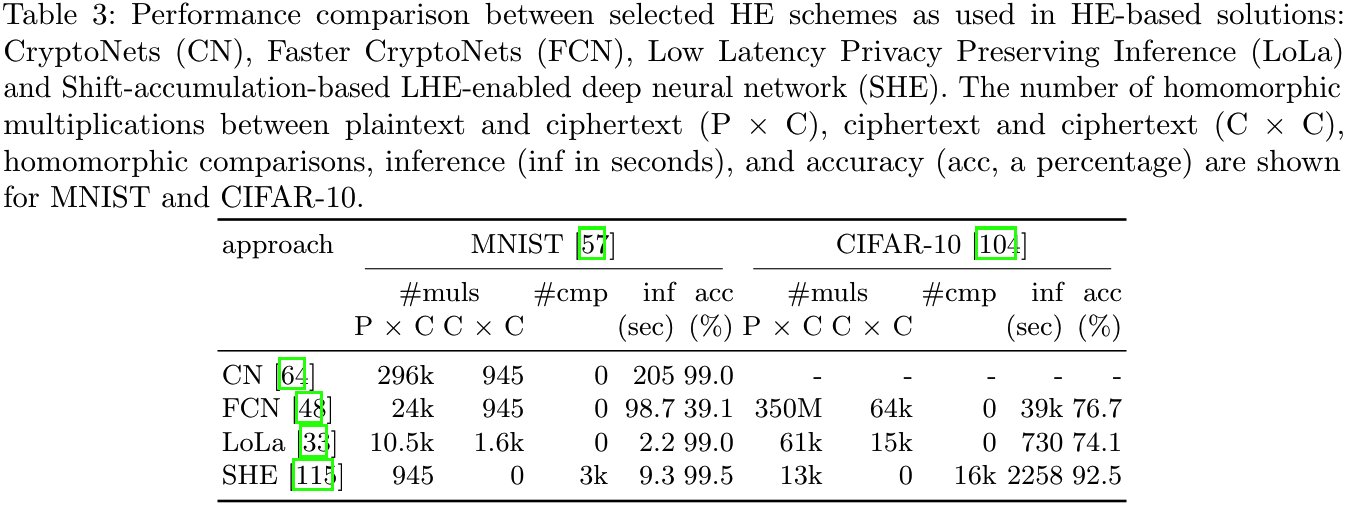
    image-20221031203518030

    从SHE来看, 虽然FHE变得越来越快, 准确度也在提高, 但单次推理所消耗的时间仍比较长, 因此实用性较差.

    3.2 混淆电路(GC)

    如果所涉及的数据都是定长的, 则NN的所有运算都可以用布尔电路来实现, 并使用混淆电路来解决SNNI问题, 此时不能保护NN架构信息, 安全性由混淆电路保证, 但效率可能会很低. 第一个主要使用GC来解决SNNI问题的工作是DeepSecure[3], 使用了Free-XOR和独立于GC的预处理技术, 利用尽可能少数量的非XOR门的基本模块来构造经典NN. 此外, 还有基于二值NN的工作XONN, 利用GC来评估非线性层的Dephi.

    3.3 加法秘密共享(ASS)

    评估非线性层需要秘密份额之间的加法和乘法. 两方计算时秘密份额的加法是平凡的, 秘密份额的乘法则需要借助Bever三元组.

    3.3.1 生成Beaver三元组

    Beaver三元组不依赖于输入, 因此可以在离线预处理阶段生成. 如果只有两方, 生成Beaver三元组的方式有两种: 同态加密和不经意传输. 此外, 如果有额外的不参与在线阶段计算的第三方, 则可让其生成Beaver三元组提高计算效率, 如Chameleon. 若使用2-out-of-3秘密共享, 则不需要Beaver三元组即可计算乘法, 如Falcon.

    3.3.2 评估非线性层

    • 多项式近似, 例子: SecureML、Delphi等;
    • 把通用密码协议用于某个特定功能, 但主要方法仍是ASS, 例子: SecureML, MiniONN使用了GC, CrypTFlow2使用了OT;
    • 其他专用方案, 例子: SiRnn使用lookup table和迭代近似(iterative approximation)来计算指数函数和反函数, 从而可通过ASS来计算Sigmoid函数, Faclon使用迭代近似来计算除法, 使用二叉搜索(binary search)来计算max-pooling.

    3.4 混合协议方案

    HE、GC、ASS都有一些缺点, 限制了某些层的适用性, 由于这些缺点与不同类型层相关, 因此可以考虑将多种技术进行组合, 使得NN的每层都使用最合适的技术, 尽管这将使得方案变成交互式的. 多数情况下ASS被用作框架, 辅以其他技术, 用于在线阶段不同类型的层的安全计算, 例子:

    • SecureML和MiniONN将ASS用于线性层, 将GC用于非线性层;
    • Chameleon对线性层使用ASS, 对ReLU激活函数使用GMW协议, 对argmax使用GC;
    • Gazelle将HE用于线性层, 将GC用于非线性层;
    • CrypTFlow2将HE或OT用于线性层, 将ASS与专用子协议用于非线性层;
    • Delphi使用ASS用于线性层和平方激活, 使用GC进行ReLU激活.

    3.5 其他方面

    3.5.1 不经意传输的使用

    OT通常是许多SNNI方法的重要组成部分:

    • 混淆电路的计算;
    • 生成Beaver三元组;
    • 可构造专用子协议, 用于评估秘密共享形式的非线性层, 如CrypTFlow2.

    3.5.2 数字编码

    理论上NN的输入和输出以及权重和其他参数可以是任何实数, 但在计算机实现中, 所有这些数字都使用有限位来表示, 选择数字表示方案取决于如下几个方面:

    • 表示类型: 浮点(floating-point)、定点(fixed-point)、整数(integer);
    • 有符号(signed)/无符号(unsigned);
    • 位宽(bitwidth, 总位长);
    • 比例(scale, 也称为精度, 小数部分的位数).

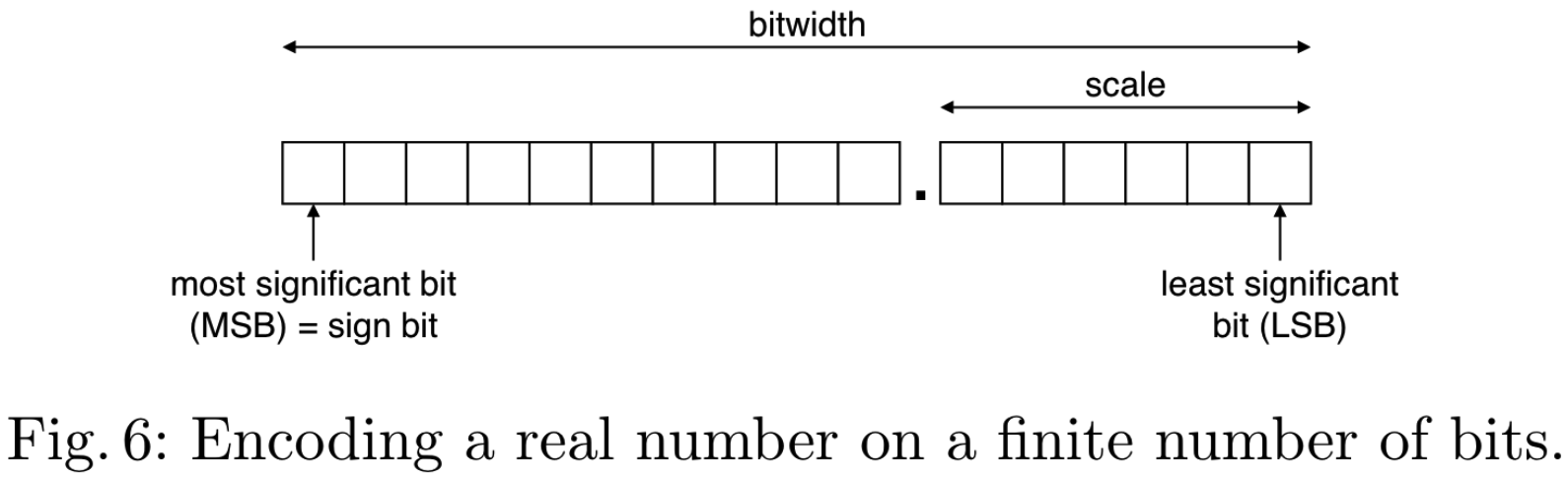
    image-20221031222913369

    这些方面的不同选择可能会造成重大影响, 从而导致效率和准确性之间的不同权衡. 特别是减小位宽可以显著提高效率, 这取决于所使用的技术, 例如使用GC时减少位宽可使电路规模减小, 从而只需更少的计算和更少的通信, 但可能会限制可实现的准确性.

    计算机通常天然支持给定位宽运算, 利用这种硬件支持的位宽可以实现更简单高效的方案. 例如: Delphi和Falcon使用32位的固定位宽, 而SecureML和SecureNN使用64位的固定位宽, 此外位宽不需要在整个NN中都是均匀的, 例如SiRnn引入的动态调整位宽的协议. 某些运算可能会改变位宽, 此时需要额外进行截断运算.

    对于小数部分的精度, 有不同的解决方案, 例如具有统一精度的定点表示的有Delphi和Falcon, 动态确定精度的有CrypTFlow2, 还有一些方案使用整数以固定位数表示, 但要确保没有溢出, 例如MiniONN.

    对于有符号数的编码, 通常使用二进制补码(two's complement), 在评估ReLU时需要确定数字是否为正数, 在二进制补码中这归结为确定数字的最高有效位.

    在HE情况下, 几种加密方案都基于多项式, 明文被编码为多项式系数. 为充分利用消息空间, 一些方法(如CryptoNets)通过中国剩余定理将多个数字打包为一个系数, 用多个系数来表示一个数字. 通过使用FHE方法, 可以通过以定点表示来处理这些数字, 这需要将数字映射到实践中所使用的多项式环中, [4]给出了一种为同态函数评估设计的定点数有效编码方法.

    3.5.3 并行化

    使用密码学协议使得利用并行化计算更具挑战性. 一些同态加密方案支持SIMD处理, 从而对同一批次不同输入执行相同的操作. 离线阶段也可以利用并行化计算, 例如SecureML中生成向量化的Beaver三元组, MiniONN也使用了类似的方法.

    3.5.4 关联随机性

    为了茫化秘密, 有些方案使用了关联随机数, 即由不同方拥有满足某种关系的随机数. 典型的例子是Beaver三元组、ABY3和Falcon中使用的Zero sharing.

    生成关联随机性主要有两种方法:

    • 使用PRG, PRF, HE或OT等密码学协议来生成, 例如Falcon使用预共享密钥的PRF来生成不同类型的关联随机性;
    • 使用额外第三方来生成, 例如Chameleon使用半诚实第三方生成随机种子发给两方, 然后两方本地通过PRG生成.

    3.5.5 神经架构搜索(NAS)

    SNNI的一些方案也对NN架构进行了修改, 事实上在普通环境中使用表现良好的架构可能不是SNNI的最佳选择. 找到最佳的NN架构是一个繁琐的过程, 涉及尝试许多不同的候选架构、训练并评估实现的准确性. 此过程可以通过神经网络架构搜索(Neural Architecture Search, NAS)算法自动执行.

    例如: Delphi将NAS用于特定目的: 它使用平方函数替换了NN中的一些ReLU激活, 旨在找到准确性和推理效率之间的良好权衡, 要替换哪些ReLU由NAS决定. NASS进一步使用NAS, 在寻找安全推理的最佳神经架构时, NASS会考虑不同密码原语的开销, 作为搜索过程的一部分, NASS还会自动调整用于NN线性层的HE参数[5]. 此外, HEMET也遵循类似的方法[6].

    3.5.6 多项式近似

    HE和ASS适合评估多项式. 对于非多项式函数, 可以使用适当的多项式近似代替, 但这将会导致高阶多项式开销大的问题, 因为乘法所需的开销大, 而低阶多项式近似效果很差. 解决这个问题的唯一可能方法是使用分段多项式近似. 例子: SecureML, MiniONN, Delphi.

    3.5.7 加速卷积

    卷积可以用矩阵乘法表示, 从而可以像处理全联接层一样处理卷积层, 理论上很方便, 但可能导致实现效率低下, 特别是在ASS的框架下使用Beaver三元组来实现矩阵乘法, 相同的矩阵元素被多个Beaver三元组所茫化从而导致Beaver三元组的浪费. CryTFlow的Porthos组件对此进行了优化, 以减少卷积所需的Beaver三元组数量. 而CrypTFlow2中的卷积使用了HE实现, 通过巧妙地使用SIMD, 减少HE rotation操作次数来加速卷积计算.

    3.5.8 安全性分析

    在大多数情况下, 基于MPC的解决方案的安全性(输入隐私性)建立在通用可组合(Universal Composability, UC)框架下, 依赖于其构造模块的安全性和可组合性. 而基于HE的解决方案的安全性通常基于困难问题, 如Ring-LWE问题等.

    3.6 其他方法

    • 模型拆分: 将NN拆分为多个部分分配给不同的参与方, 从而限制每方得到的知识.
    • 可信执行环境: 可在不受信任的环境中实现安全计算, 使用硬件隔离和加密技术来保证数据机密性和执行的完整性, 几乎没有通信开销, 能以原生速度运行. 缺点: 存在侧信道攻击且必须信任设备的生产厂商. 例子: Intel SGX和面向移动设备部署的ARM TrustZone.
    • 编译器: 将机器学习代码转换为安全协议代码的编译器. 例子: Rosetta, secureTF, MP2ML, CHET, EzPC, CrypTen. 还有一些编译器将高级编程语言转换为电路格式, 然后可以基于HE, GC和ASS的安全计算框架进行评估. 例子: HyCC.

    4. SNNI方法的实现

    image-20221101104935350

    5. 实验评估

    5.1 机器学习问题, NN和数据集

    大多数SNNI的工作集中在图像分类问题上, 因此CNN更常见. 根据CNN规模, 常见的CNN可以分为:

    • 小规模: LeNet(7层), AlexNet(8层);
    • 大规模: VGG16、VGG19、ResNet50、DenseNet121和SqueezeNet.

    常用数据集: MNIST, CIFAR-10.

    其他类型的NN还有:

    • 循环神经网络(Recurrent Neural Networks, RNN): 对顺序数据(如音频/传感器数据等)进行分类.
    • 图神经网络(Graph Neural Networks, GNN): 对节点组成的数据及其空间位置信息进行分类.

    5.2 技术设置

    实验环境: 本地模拟LAN/WAN、云服务器环境的LAN/WAN.

    • WAN: 带宽9~70MB/s, 延迟60ms;
    • LAN: 带宽1GB/s, 延迟<1ms.

    5.3 评估指标

    • 执行时间/时延(execution time/latency): 执行一次推理所消耗的时间. 此外, 批处理方法可用平均时间.
    • 通信量(communication): 各参与方之间传输的总字节量. 此外, 批处理方法可用平均通信量.
    • 吞吐量(throughput): 单位时间内的推理次数, 衡量批处理效果的指标.
    • 准确率(accuracy): 限制和修改NN可能会影响准确性, 因此需要对方法的准确率进行评估.

    5.4 对比

    当要说明一种新方法改进了现有技术时, 需要对两者进行对比, 此时需要面临如下问题:

    • 比较维度应一致
    • 安全属性难以量化
    • 只进行少量实验或只考虑效率和准确性难以表明方案的优劣

    6. 未来研究方向

    1. SNNI方法的特征:
      • 安全性与效率的权衡: 如何同时实现高效性和高安全级别?
      • 具体应用场景的影响: 具体应用如何影响不同方法的适用性?
      • 物联网和边缘计算中的SNNI: 当可用资源受限时SNNI方案的构造?
      • 安全推理友好的NN和训练: 安全推理与安全训练的集成优化问题?
      • 抵御黑盒攻击: 大多数SNNI方法不能防止黑盒攻击?
    2. 解决方案:
      • 新的构造模块? 例如: Silent OT的应用.
      • 模块化解决方案: 将模块化方案扩展到支持任意数量的计算方, 支持不同敌手模型和保密目标, 使用广泛的模型架构等, 提升用户需求的灵活性?
      • 解决方案的可扩展性: 现有SNNI方案的内存、计算和通信要求很高, 如何扩展到多方? 如何在多个节点之间摊销这些开销?
    3. 实现:
      • ML框架集成和统一的API
      • GPU支持
      • 容器构建: 容易重现实验并对性能进行公平比较
    4. 解决方案的评估:
      • 改善对比方法, 确保公平比较
      • 更多样的基准
      • 现实技术设置
      • 考虑超越效率的指标: 包括能耗、安全性、隐私性和可用性.

    参考文献

    [1] Barni, M., Orlandi, C., and Piva, A. A privacy-preserving protocol for neural-network-based computation. In MM&Sec (2006), ACM, pp. 146–151.

    [2] Barni, M., Orlandi, C., and Piva, A. A privacy-preserving protocol for neural-network-based computation. In MM&Sec (2006), ACM, pp. 146–151.

    [3] Rouhani, B. D., Riazi, M. S., and Koushanfar, F. Deepsecure: scalable provably-secure deep learning. In DAC (2018), ACM, pp. 2:1–2:6.

    [4] Bonte, C., Bootland, C., Bos, J. W., Castryck, W., Iliashenko, I., and Vercauteren, F. Faster homomorphic function evaluation using non-integral base encoding. In CHES (2017), Springer, pp. 579–600.

    [5] Bian, S., Jiang, W., Lu, Q., Shi, Y., and Sato, T. NASS: optimizing secure inference via neural architecture search. In ECAI (2020), vol. 325 of Frontiers in Artificial Intelligence and Applications, IOS Press, pp. 1746–1753.

    [6] Lou, Q., and Jiang, L. HEMET: A homomorphic-encryption-friendly privacy-preserving mobile neural network architecture. In ICML (2021), vol. 139 of Proceedings of Machine Learning Research, PMLR, pp. 7102–7110.


    本文标题: Towards Practical Secure Neural Network Inference: The Journey So Far and the Road Ahead
    本文作者: 云中雨雾
    本文链接: https://weiviming.github.io/16675243955254.html
    本站文章采用 知识共享署名4.0 国际许可协议进行许可
    除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
    最后编辑时间: 2022-11-04T09:13:15+08:00