Communication-Efficient (Client-Aided) Secure Two-Party Protocols and Its Application

今天给大家带来的是发表于Financial Cryptography and Data Security 2020 (FC'20)的文章Communication-Efficient (Client-Aided) Secure Two-Party Protocols and Its Application, 原文链接: https://arxiv.org/pdf/1907.03415

Abstract

基于秘密共享的多方计算协议(SS-MPC)可以很容易实现高吞吐量, 但通常通信轮次较大, 是WAN高延迟网络环境的主要性能瓶颈, 故减少SS-MPC协议的通信轮次是提升MPC效率的关键所在, 换而言之, 应让MPC的电路尽可能地浅. 为此, 本文主要专注于减少通信轮次, 利用Beaver三元组扩展(Beaver triple extension, BTE)构造了半诚实安全的通信高效的两方计算协议, 可对多扇入门(mult-fan-in gates)进行高效计算, 并给出了一些应用. 例如, 对于比较协议, 只需通信3轮, 比之前相同设定下的工作通信量也减少了38.4%, 总在线执行时间减少了56.1%, 虽然计算开销比以往工作要高, 但本文表明在WAN下这对整体在线性能影响很小.

Preliminaries

秘密共享方案: $\mathbb Z_{2^n}$上的两方加法秘密共享$(2,2)$-additive secret sharing, $[\![x]\!]=([\![x]\!]_0,[\![x]\!]_1)$.
安全模型: 两方半诚实安全模型
客户端辅助(client-aided)模型, 设客户端不与任何计算方共谋, 主要负责生成并分发Beaver三元组以提升离线阶段的效率.

Core Tools for Round-Efficient Protocols

$N$-fan-in MULT/AND via $N$-Beaver Triple Extension

令$N$是正整数, $\mathcal M=\mathbb Z_{M}$, 其中$M=2^n$. 记$[1,N]=\{1,2,\cdots,N\}$. 定义客户端辅助协议来生成$N$-BTE的方法如下:

对于$\ell=1,\cdots,N$, 客户端从$\mathcal M$中随机选取$[\![a_{\{\ell\}}]\!]_0$和$[\![a_{\{\ell\}}]\!]_1$, 设$a_{\{\ell\}}\leftarrow[\![a_{\{\ell\}}]\!]_0+[\![a_{\{\ell\}}]\!]_1$. 对于满足$|I|\geq2$的每个$I\subseteq[1,N]$, 通过设定$a_I\leftarrow\prod_{\ell\in I}a_{\{\ell\}}$, 客户端随机选取$[\![a_I]\!]_0\in\mathcal M$, 并设定$[\![a_I]\!]_1\leftarrow a_I-[\![a_I]\!]_0$.
客户端发送所有的$[\![a_I]\!]_0$给$P_0$和所有的$[\![a_I]\!]_1$给$P_1$.

对于$\ell=1,\cdots,N$, 令$([\![x_\ell]\!]_0,[\![x_\ell]\!]_1)$为给定第$\ell$个秘密输入值$x_\ell\in\mathcal M$的份额, 则多扇入MULT/AND门的计算协议的计算方式如下:

客户端利用上述协议生成并分发$N$-BTE$([\![a_I]\!]_0)_I$和$([\![a_I]\!]_1)_I$给两方.
对于$k=0,1$, $P_k$计算并发送$[\![x_\ell']\!]\leftarrow[\![x_\ell]\!]_k-[\![a_{\{\ell\}}]\!]$给$P_{1-k}$.
对于$k=0,1$, $P_k$计算$x_\ell'\leftarrow[\![x_\ell']\!]_{1-k}+[\![x_\ell']\!]_k$.
$P_0$计算并输出$[\![y_0]\!]\leftarrow\prod_{\ell=1}^Nx_{\ell}'+\sum_{\emptyset\neq I\subseteq[1,N]}(\prod_{\ell\in[1,N]\setminus I}x_\ell')[\![a_I]\!]_0$, $P_1$计算并输出$[\![y_1]\!]\leftarrow\sum_{\emptyset\neq I\subseteq[1,N]}(\prod_{\ell\in[1,N]\setminus I}x_\ell')[\![a_I]\!]_1$.

可以看到上述协议只需1轮通信, 且不依赖于$N$, 适合WAN设定, 但缺点是内存消耗和计算开销与$N$成指数级别增长, 因此本文在实际应用中取$N\leq 9$. 当使用$L$扇入MULT/AND门($L\leq N$)时, 需要$\frac{\lceil\log N\rceil}{\lfloor \log L\rfloor}$轮通信来计算$N$扇入MULT/AND.

More Techniques for Reducing Communication Rounds

One Weights At Most One: 设$P_0$和$P_1$分别持有$x$的份额布尔份额$[\![x]\!]_0^\mathsf B$和$[\![x]\!]_1^\mathsf B$, 若$x$的汉明重量至多为1, 则两方可以通过本地计算其份额比特的$\mathsf{XOR}$来得到$x=_?0$的份额. 因为若$x\neq0$, 则$P_0$计算的$\bigoplus[\![x]\!]_0^\mathsf B$和$P_1$计算的$\bigoplus[\![x]\!]_1^\mathsf B$之中至少有一个为1, 从而两者份额比特的$\mathsf{XOR}$结果为1.
Arithmetic Blinding: 设两个客户端也是计算参与方, 则当它们执行计算时已知秘密本身, 与客户端辅助2PC计算的情况不同, 此时$P_0$和$P_1$随机将其各自持有的秘密$x$和$y$分割为$x_0,x_1$和$y_0,y_1$, 然后$P_0$发送$x_1$给$P_1$, $P_1$发送$x_0$给$P_0$. 若$P_0$和$P_1$在之前已经分别得到了$a_0,b_0,c_0$和$a_1,b_1,c_1$, 则$P_0$和$P_1$可通过标准乘法协议来计算$[\![z]\!]=xy$, 过程如下:
1. (预计算阶段)$P_0$将$b_0$发给$P_1$, $P_1$将$a_1$发给$P_0$;
2. (在线阶段)$P_0$本地计算$x-a=x-(a_0+a_1)$并发给$P_1$, $P_1$本地计算$y-b=y-(b_0+b_1)$并发给$P_0$.
3. 对$i=0,1$, $P_i$本地计算$[\![z]\!]_i=i(x-a)(y-b)+(x-a)b+(y-b)a+c_i$.
可以看到在线阶段的通信量相比客户端不为计算方的情况减少了一半.
Trivial Sharing: 考虑输入方不为计算方的设定, 则此时与标准的客户端辅助2PC相同. 这种情况下可以使用份额$[\![b]\!]_i(i\in\{0,1\})$本身作为计算的秘密值, 另一方的份额看成$[\![0]\!]_{1-i}$. 这可以结合BTE进一步优化2PC计算协议的通信轮次.

Communication-Efficient Protocols

下面只考虑$\mathbb Z_{2^{16}}$上$N\leq5$的情况, 类似地可以实现相同通信轮次的$\mathbb Z_{2^{32}}$上$N\leq7$和$\mathbb Z_{2^{64}}$上$N\leq9$的情况.

Equality Check Protocol

给定$[\![x]\!]^\mathsf A$和$[\![y]\!]^\mathsf A$, 相等检测协议计算$[\![z]\!]^\mathsf B\leftarrow\mathsf{Equality}([\![x]\!]^\mathsf A,[\![y]\!]^\mathsf A)$, 其中$z=1$当且仅当$x=y$. 协议的主要设计思路是首先计算$t=x-y$, 然后计算$t$的所有比特的OR是否为0. 直接使用$16\text{-}\mathsf{OR}$来计算是不现实的, 本文中使用$4\text{-}\mathsf{OR}$, 如此协议只需通信$\log_{4}16=2$轮. 一般而言, 当秘密份额空间为$\mathbb Z_{2^n}$, 并使用$N\leq L$的$N\text{-}\mathsf{OR}$时, $\mathsf{Equality}$所需的通信轮次为$\frac{\lceil\log n\rceil}{\lfloor \log L\rfloor}$. 协议构造如下:

Overflow Detection Protocol

为了构造算术溢出检测协议$\mathsf{Overflow}$, 首先需要构造最高位非零比特抽取协议$\mathsf{MSNZB}$, 即$\mathsf{MSNZB}([\![x]\!]^\mathsf B=[[\![x[15]]\!]^\mathsf B,\cdots,[\![x[0]]\!]^\mathsf B])$, 查找$x$的第一个1所在位置, 输出布尔份额向量$[\![z]\!]^\mathsf B=[[\![z[15]]\!]^\mathsf B,\cdots,[\![z[0]]\!]^\mathsf B]$. 例如$x=00101$, 则$z=00100$.

为了秘密计算$x$中第一个1的位置, 引入prefix-$\mathsf{OR}$运算, 步骤如下:

通过$2\text{-}\mathsf{OR}$将最左边的1后面的比特全部置为1, 得到$x'=0\cdots011\cdots1$.
计算$z=x'\oplus(x'\gg1)$.

例如: $x=00101$, 则$x'=00111$, 于是有$z=00111\oplus00011=00100$.

通过$2\text{-}\mathsf{OR}$, 即使并行也需要通信4轮, 若改为$4\text{-}\mathsf{OR}$, 使用多扇入prefix-$\mathsf{OR}$运算则只需2轮通信, 但由于需要计算多次$4\text{-}\mathsf{OR}$, 因此计算成本将显著增大. 为在保留通信轮次的前提下优化计算, 使用分块的思想, 将比特串进行分块, 然后分别计算每块的$\mathsf{MSNZB}$. 完整协议过程如下:

有了$\mathsf{MSNZB}$, 则可根据输出所对应明文的汉明重量至多为1的特点来构造算术溢出检测协议$\mathsf{Overflow}([\![x]\!]^\mathsf A,k)$, 该协议输出$[\![z]\!]^\mathsf B$, 其中$z=1$当且仅当$([\![x]\!]_0^\mathsf A\bmod2^k+[\![x]\!]_1^\mathsf A\bmod2^k)\geq2^k$.

[1]的做法: 检查$u=(-[\![x]\!]_1\bmod2^k)$中是否存在1, 若存在则看1的位置与$d=(([\![x]\!]_0\bmod2^k)\oplus(-[\![x]\!]_1\bmod2^k))$的$\mathsf{MSNZB}$是否相同. 使用本文的两轮$\mathsf{MSNZB}$, 这种做法仍需要通信3轮, 额外的一轮是需要计算$2\text{-}\mathsf{AND}$.

本文的做法如下:

可以看到上述协议通过使用$N\text{-}\mathsf{AND}$, 步骤2和步骤6各需1轮通信, 因此总通信轮次为2. 类似地,

若份额空间为$\mathbb Z_{2^{32}}$, 则需要$N\leq7$的$N\text{-}\mathsf{AND}$门来构造两轮$\mathsf{Overflow}$;
若份额空间为$\mathbb Z_{2^{64}}$, 则需要$N\leq9$的$N\text{-}\mathsf{AND}$门来构造两轮$\mathsf{Overflow}$.

此外, 可以构造只需通信1轮的$\mathsf{Overflow}$协议, 设$\chi[P]$是表示条件$P$是否成立的比特值, 若成立则取值为1. 令$\mathsf{Overflow}(a,b;c)=\chi[a+b\geq c]$, 并设$n_1$和$n_2$是满足$n=n_1+n_2$的参数, 则1轮的$\mathsf{Overflow}$协议过程如下:

对于$i=0,1$, $P_i$记$[\![x]\!]_i^\mathsf A=y_i||z_i$, 其中$y_i=\mathsf{MSB}(x_i)$, $z_i=\mathsf{LSB}(x_i)$;
对于每个$a_1=1,\cdots,2^{n_1}-1$,
- $P_0$设定$\alpha_0^{\langle a_1;1\rangle}\leftarrow\chi[y_0=a_1]$, $\alpha_0^{\langle a_1;2\rangle}\leftarrow0$;
- $P_1$设定$\alpha_1^{\langle a_1;1\rangle}\leftarrow0$, $\alpha_1^{\langle a_1;2\rangle}\leftarrow\chi[y_1\geq2^{n_1}-a_1]$.
- 对$j=1,2$, 令$[\![\alpha^{\langle a_1;j\rangle}]\!]^\mathsf B=(\alpha_0^{\langle a_1;j\rangle},\alpha_1^{\langle a_1;j\rangle})$.
对每个$a_2=1,\cdots,2^{n_2}-1$和$j=0,\cdots,n_1-1$,
- $P_0$设定$\beta_0^{\langle\alpha_2;j\rangle}\leftarrow\begin{cases}y_0[j],&\text{if }y_0\neq0\text{ and }z_0=a_2,\\1,&\text{otherwise},\end{cases}$, 其中$y_0[j]$表示$y_0$的第$j$个比特.
- $P_1$设定$\beta_1^{\langle\alpha_2;j\rangle}\leftarrow\begin{cases}y_1[j],&\text{if }y_1\neq0\text{ and }z_1\geq2^{n_2}-a_2,\\1,&\text{otherwise},\end{cases}$.
- 令$[\![\beta^{\langle\alpha_2;j\rangle}]\!]^\mathsf{B}=(\beta_0^{\langle\alpha_2;j\rangle},\beta_1^{\langle\alpha_2;j\rangle})$.
对于每个$a_3=1,\cdots,2^{n_2}-1$,
- $P_0$设定$\gamma_0^{\langle a_3;1\rangle}\leftarrow\chi[y_0=0]$, $\gamma_0^{\langle a_3;2\rangle}\leftarrow\chi[y_0=2^{n_1}-1]$, $\gamma_0^{\langle a_3;3\rangle}\leftarrow\chi[z_0=a_3]$, $\gamma_0^{\langle a_3;4\rangle}\leftarrow0$;
- $P_1$设定$\gamma_1^{\langle a_3;1\rangle}\leftarrow\chi[y_1=0]$, $\gamma_1^{\langle a_3;2\rangle}\leftarrow\chi[y_1=2^{n_1}-1]$, $\gamma_1^{\langle a_3;3\rangle}\leftarrow0$, $\gamma_1^{\langle a_3;4\rangle}\leftarrow\chi[z_1\geq2^{n_2}-a_3]$.
- 对$j=1,2,3,4$, 令$[\![\gamma^{\langle a_3;j\rangle}]\!]^\mathsf B=(\gamma_0^{\langle a_3;j\rangle},\gamma_1^{\langle a_3;j\rangle})$.
两方并行计算如下:
- 对于每个$a_1=1,\cdots,2^{n_1}-1$, 计算$[\![b_1^{\langle a_1\rangle}]\!]^\mathsf B\leftarrow2\text{-}\mathsf{AND}([\![\alpha^{\langle a_1;1\rangle}]\!]^\mathsf B,[\![\alpha^{\langle a_1;2\rangle}]\!]^\mathsf B)$;
- 对于每个$a_2=1,\cdots,2^{n_2}-1$, 计算$[\![b_2^{\langle a_2\rangle}]\!]^\mathsf B\leftarrow n_1\text{-}\mathsf{AND}([\![\beta^{\langle \alpha_2;0\rangle}]\!]^\mathsf B,[\![\beta^{\langle \alpha_2;1\rangle}]\!]^\mathsf B,\cdots,[\![\beta^{\langle \alpha_2;n_1-1\rangle}]\!]^\mathsf B)$;
- 对于每个$a_3=1,\cdots,2^{n_3}-1$, 计算$[\![b_3^{\langle a_3\rangle}]\!]^\mathsf B\leftarrow4\text{-}\mathsf{AND}([\![\gamma^{\langle a_3;1\rangle}]\!]^\mathsf B,[\![\gamma^{\langle a_3;2\rangle}]\!]^\mathsf B,[\![\gamma^{\langle a_3;3\rangle}]\!]^\mathsf B,[\![\gamma^{\langle a_3;4\rangle}]\!]^\mathsf B)$;
$P_i$本地计算并输出$[\![d_i]\!]^\mathsf B\leftarrow\bigoplus_{a_1=1}^{2^{n_1}-1}[\![b_1^{\langle a_1\rangle}]\!]_{i}^\mathsf B\oplus\bigoplus_{a_2=1}^{2^{n_2}-1}[\![b_2^{\langle a_2\rangle}]\!]_{i}^\mathsf B\bigoplus_{a_3=1}^{2^{n_2}-1}[\![b_3^{\langle a_3\rangle}]\!]_{i}^\mathsf B$.

可以看到上述协议只有步骤5需要1轮通信, 但计算开销和通信量开销都很大.

Less-Than Comparison Protocol

给定$[\![x]\!]^\mathsf{A},[\![y]\!]^\mathsf A$, Less-Than比较协议计算$[\![z]\!]^\mathsf{B}\leftarrow\mathsf{Comparison}([\![x]\!]^\mathsf A,[\![y]\!]^\mathsf{A})$, 其中$z=1$当且仅当$x<y$. 对$i\in\{0,1\}$, 协议过程如下:

对于$x,y,d=x-y$, $P_i$分别计算
- $[\![x']\!]^\mathsf B=[\![\mathsf{Overflow}(x,2^{n-1})]\!]^\mathsf B\oplus[\![\mathsf{MSB}(x)]\!]^\mathsf B$,
- $[\![y']\!]^\mathsf B=[\![\mathsf{Overflow}(y,2^{n-1})]\!]^\mathsf B\oplus[\![\mathsf{MSB}(y)]\!]^\mathsf B$,
- $[\![d']\!]^\mathsf B=[\![\mathsf{Overflow}(d,2^{n-1})]\!]^\mathsf B\oplus[\![\mathsf{MSB}(d)]\!]^\mathsf B$.
$P_i$计算$[\![v]\!]^\mathsf B\leftarrow2\text{-}\mathsf{AND}(([\![x']\!]^\mathsf B\oplus[\![y']\!]^\mathsf B),[\![y']\!]^\mathsf B)$, $[\![w]\!]^\mathsf B\leftarrow2\text{-}\mathsf{AND}(\neg([\![x']\!]^\mathsf B\oplus[\![y']\!]^\mathsf B),[\![y']\!]^\mathsf B)$.
$P_i$计算$[\![z]\!]^\mathsf B=[\![v]\!]^\mathsf B\oplus[\![w]\!]^\mathsf B$.

如上协议需要3轮通信.

Boolean-to-Arithmetic Conversion Protocol and Extensions

B2A转换协议计算$[\![z]\!]^\mathsf A\leftarrow\mathsf{B2A}([\![x]\!]^\mathsf B)$, 其中$z=x$. 由于这种情况下两方已知$x$的其中一个份额, 故可以通过一个算术茫化三元组来完成转换, 其中算术茫化三元组$(a,b,c)$满足$c=ab$, $P_0$得到$(a,c_0)$, $P_1$得到$(b,c_1)$.

协议过程如下:

可以看到计算方只需1轮通信. 可以利用同样的思想来构造如下协议:

$\mathsf{BX2A}$: $[\![b]\!]^\mathsf B\times[\![x]\!]^\mathsf A=[\![bx]\!]^\mathsf A$. 过程如下:
1. $P_i$设定$[\![b]\!]_i^\mathsf A=[\![b]\!]_i^\mathsf B$.
2. $P_0$设定$[\![b']\!]_0^\mathsf A=[\![b]\!]_0^\mathsf B$, $[\![b'']\!]_0^\mathsf A=0$, $P_1$设定$[\![b']\!]_1^\mathsf A=0$, $[\![b'']\!]_1^\mathsf A=[\![b]\!]_1^\mathsf B$.
3. $P_i$计算$[\![s]\!]_i^\mathsf A\leftarrow2\text{-}\mathsf{MULT}([\![b]\!]^\mathsf A,[\![x]\!]^\mathsf A)$和$[\![t]\!]_i^\mathsf A\leftarrow3\text{-}\mathsf{MULT}([\![b']\!]^\mathsf A,[\![b'']\!]^\mathsf A,[\![x]\!]^\mathsf A)$.
4. $P_i$计算$[\![z]\!]_i^\mathsf A=[\![s]\!]_i^\mathsf A-2[\![t]\!]_i^\mathsf A$.
只需1轮通信, 记以上计算为$[\![b-2b_0b_1x]\!]^\mathsf A$. 可用于构造查表协议$\mathsf{TLU}$(结合$\mathsf{Equality}$)以及计算神经网络中的$\mathsf{ReLU}$函数.
$\mathsf{BC2A}$: $[\![b]\!]^\mathsf B\times[\![c]\!]^\mathsf B=[\![bc]\!]^\mathsf A$. 过程与$\mathsf{BX2A}$类似, 通过使用$2\text{-}\mathsf{MULT}$和$4\text{-}\mathsf{MULT}$来构造1轮通信的计算协议, 记为$[\![bc-2b_0b_1-2c_0c_1+2b_0\bar{c_0}b_1\bar{c_1}+2\bar{b_0}c_0\bar{b_1}c_1]\!]^\mathsf A$. 可用于构造三数最值索引计算协议$3\text{-}\mathsf{Argmax}$/$3\text{-}\mathsf{Argmin}$.
$\mathsf{BCX2A}$: $[\![b]\!]^\mathsf B\times[\![c]\!]^\mathsf B\times[\![x]\!]^\mathsf A=[\![bcx]\!]^\mathsf A$. 过程类似, 通过使用$3\text{-}\mathsf{MULT}$和$5\text{-}\mathsf{MULT}$来构造1轮通信的计算协议, 记为$[\![bcx-2b_0b_1x-2c_0c_1x+2b_0\bar{c_0}b_1\bar{c_1}x+2\bar{b_0}c_0\bar{b_1}c_1x]\!]^\mathsf A$. 可用于构造最值计算协议$\mathsf{Max}/\mathsf{Min}$.

The Maximum Value Extraction Protocol and Extensions

最大值抽取协议计算$[\![z]\!]^\mathsf A\leftarrow\mathsf{Max}([\![{\mathbf x}]\!]^\mathsf A)$, 其中$z$是向量$\mathbf x$中分量的最大值. 简单起见, 假设向量$\mathbf x$中有三个分量, 相应的计算协议记为$3\text{-}\mathsf{Max}$, 若直接两两比较来求解, 利用本文提出的3轮$\mathsf{Comparison}$协议和1轮$\mathsf{BX2A}$协议, 所得协议的总通信轮次为$(3+1)\times 2=8$. 主要原因是$\mathsf{Comparison}$不能并行. 为此, 本文的做法是首先用$\mathsf{Comparison}$比较所有元素的大小关系, 然后利用$\mathsf{BCX2A}$提取最大值, 如此只需4轮通信. 协议过程如下:

类似的思路可以构造最小值提取协议$3\text{-}\mathsf{Min}$. 此外, 适当修改算法5中的相应步骤, 可以得到计算最值所在索引的$\mathsf{Argmax}/\mathsf{Argmin}$协议, 修改方式如下:

将算法5第3步中计算的$[\![t[j]]\!]^\mathsf A\leftarrow\mathsf{BCX2A}([\![*]\!]^\mathsf B,[\![**]\!]^\mathsf B,[\![x]\!]^\mathsf A)$替换为$[\![t'[j]]\!]^\mathsf A\leftarrow\mathsf{BC2A}([\![*]\!]^\mathsf B,[\![**]\!]^\mathsf{B})$;
将算法5第4步修改为$P_i$计算$[\![z]\!]_i^\mathsf A\leftarrow\sum_{j=0}^2(j\cdot[\![t'[j]]\!]_i^\mathsf A)$, 这一步中$j$是公开的, 因此不需要通信.

所需通信轮次为3.

对于$N>3$时计算$N\text{-}\mathsf{Max}/\mathsf{Min}$的情形, 可以用类似的思路来构造轮高效的计算协议, 但需注意如下两点:

在$N\text{-}\mathsf{Max}/\mathsf{Min}$中需要并行执行$\mathsf{Comparison}$协议$\frac{N(N-1)}{2}$次, 而两两比较的方法只需执行$\lceil\log N\rceil$次, 因此, 本文方案的计算开销和通信量开销与$N$成指数关系.
对于较大的$N$, 不能直接使用$\mathsf{BCX2A}$或$\mathsf{BC2A}$, 若用构造$\mathsf{BCX2A}$的类似协议来计算, 则计算开销将非常巨大. 为此, 可以将算法5中的第3步分解为其他协议, 例如$(N-1)\text{-}\mathsf{AND}$和$\mathsf{BX2A}$, 如此需要更多的通信轮次来计算$N\text{-}\mathsf{Max}/\mathsf{Min}$.

Perfermance Evaluation

WAN设定: 10MB/s(=80000bits/ms)带宽, 40ms RRT延迟.

Performance of Basic Gates

下图是不同$N$下计算$N\text{-}\mathsf{AND}$的开销, 可以看到随着$N$的增大, 预处理所需时间也随之指数级膨胀. 此外, 当批次较小时, WAN的延迟主导了在线运行时间. 因此本文方案适合具有低延迟的WAN场景下的相对小的批次的2PC计算, 例如批次$\leq10^5$.

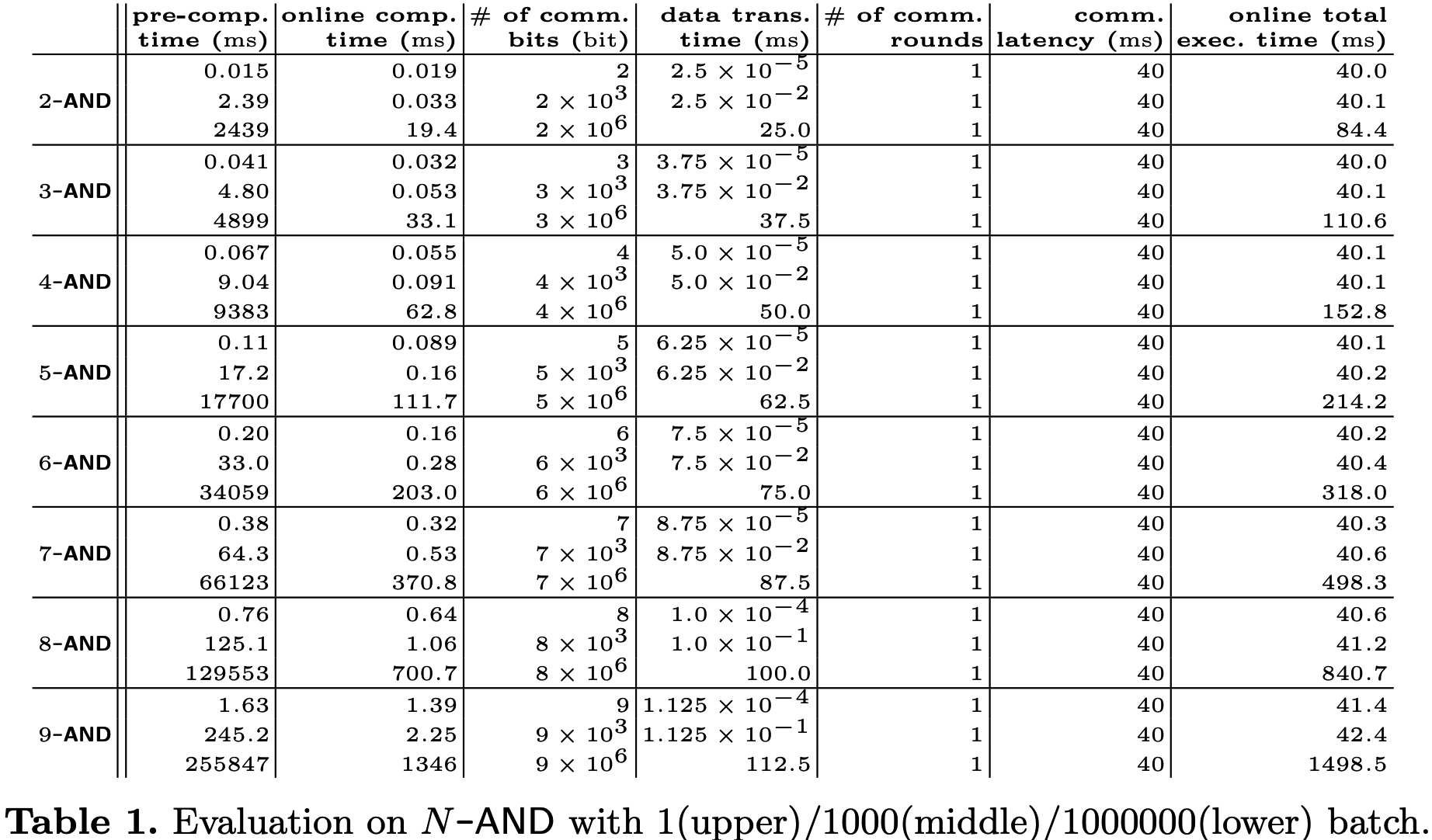
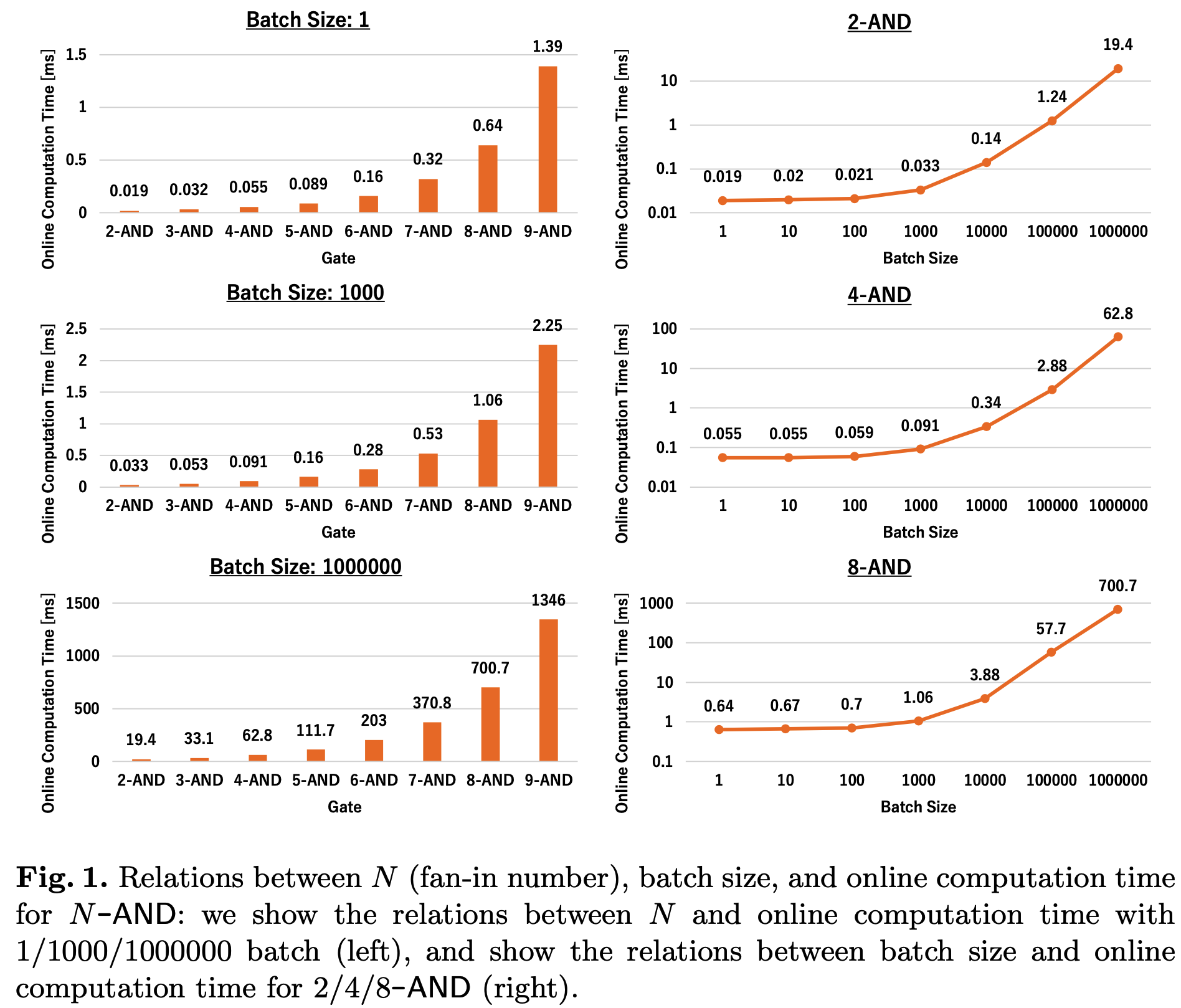
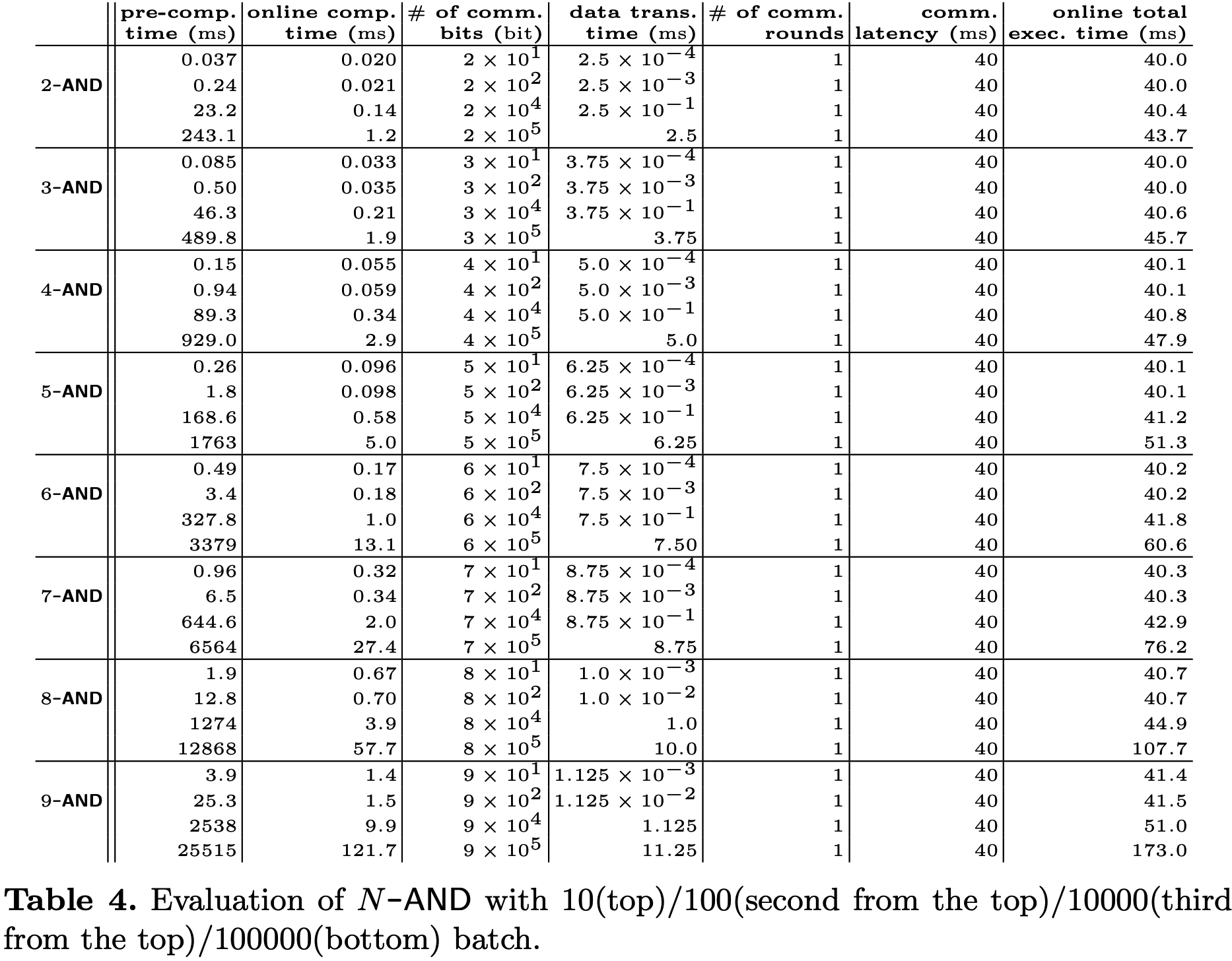
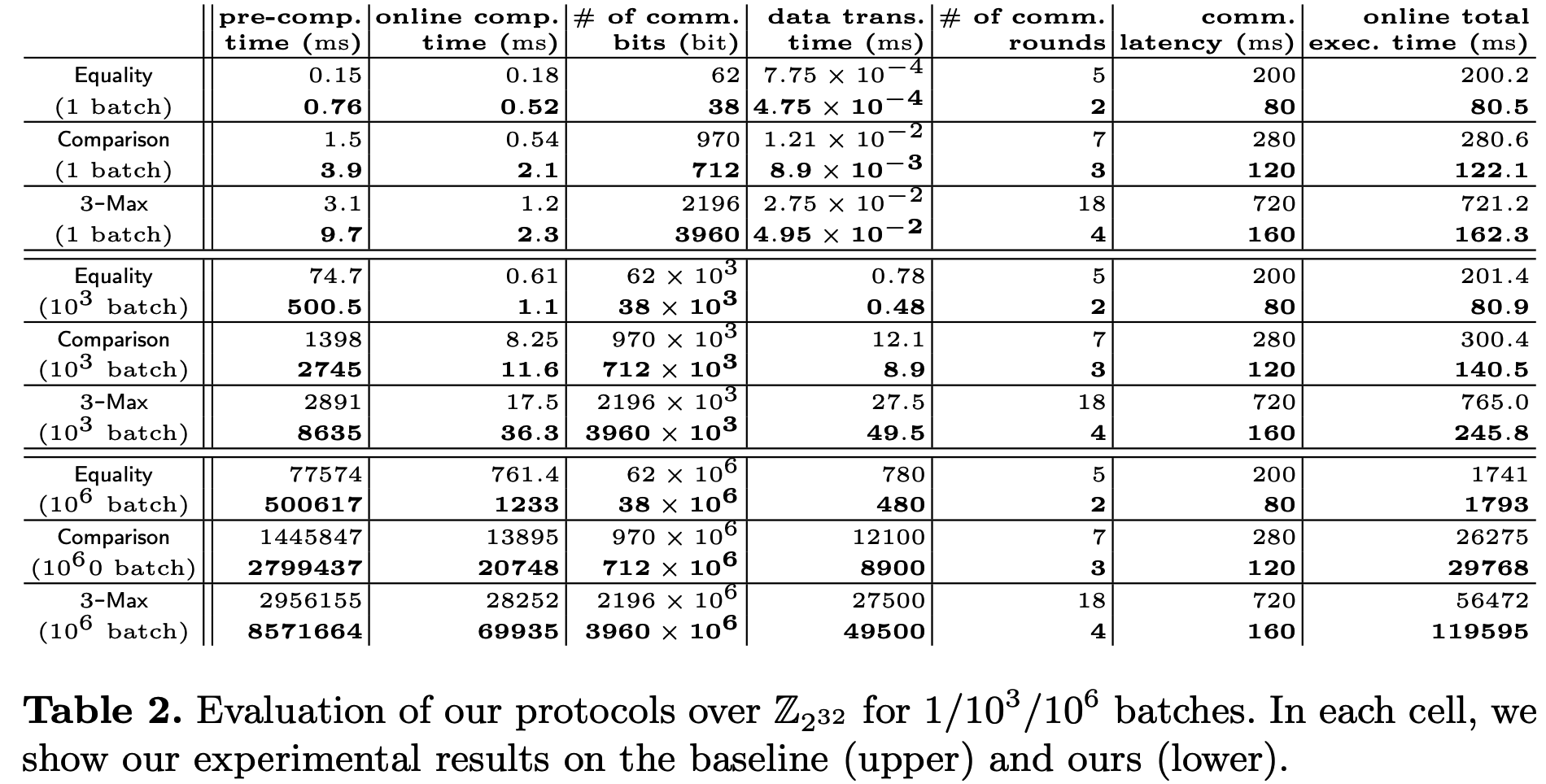
Performance of Our Protocols

协议实现方面, 主要考察了$\mathsf{Equality}$, $\mathsf{Comparison}$和$3\text{-}\mathsf{Max}$与[1]的对比. 结果如下, 可以看到在线总执行时间主导因素为WAN的延迟. 对于批次$\leq10^4$的情况下, 本文的协议比基准线更快, 主要原因是本文需要的通信轮次更少, 但由于计算开销太大, 本文方案不适合批次较大的情形.

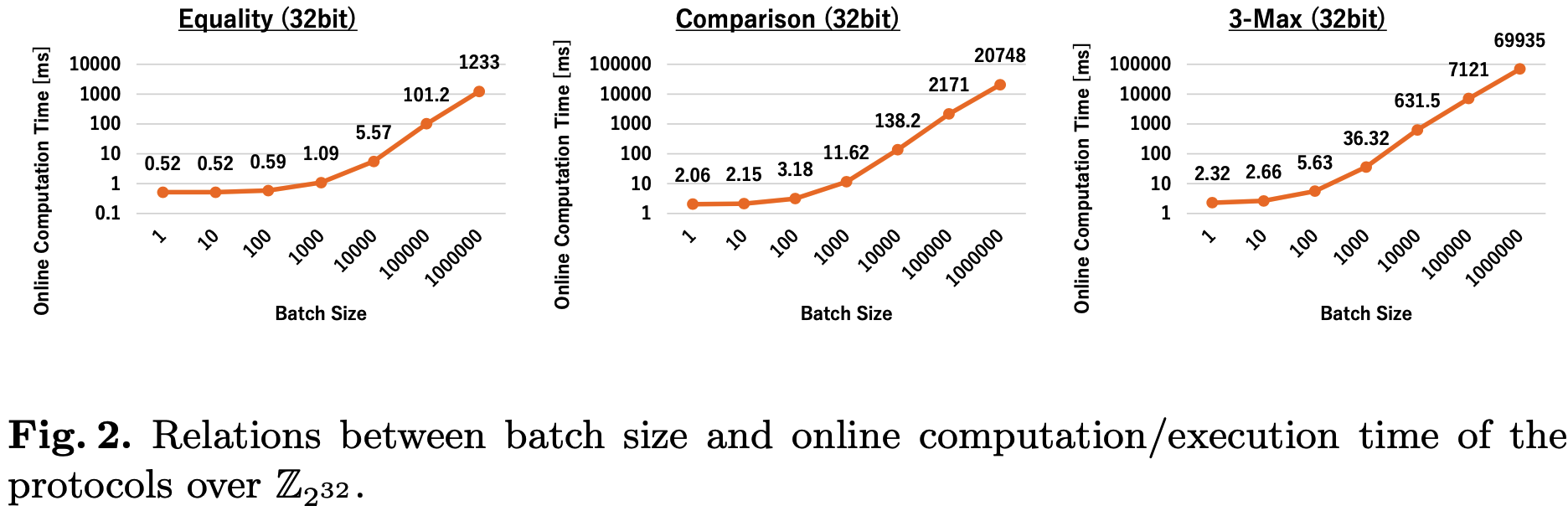
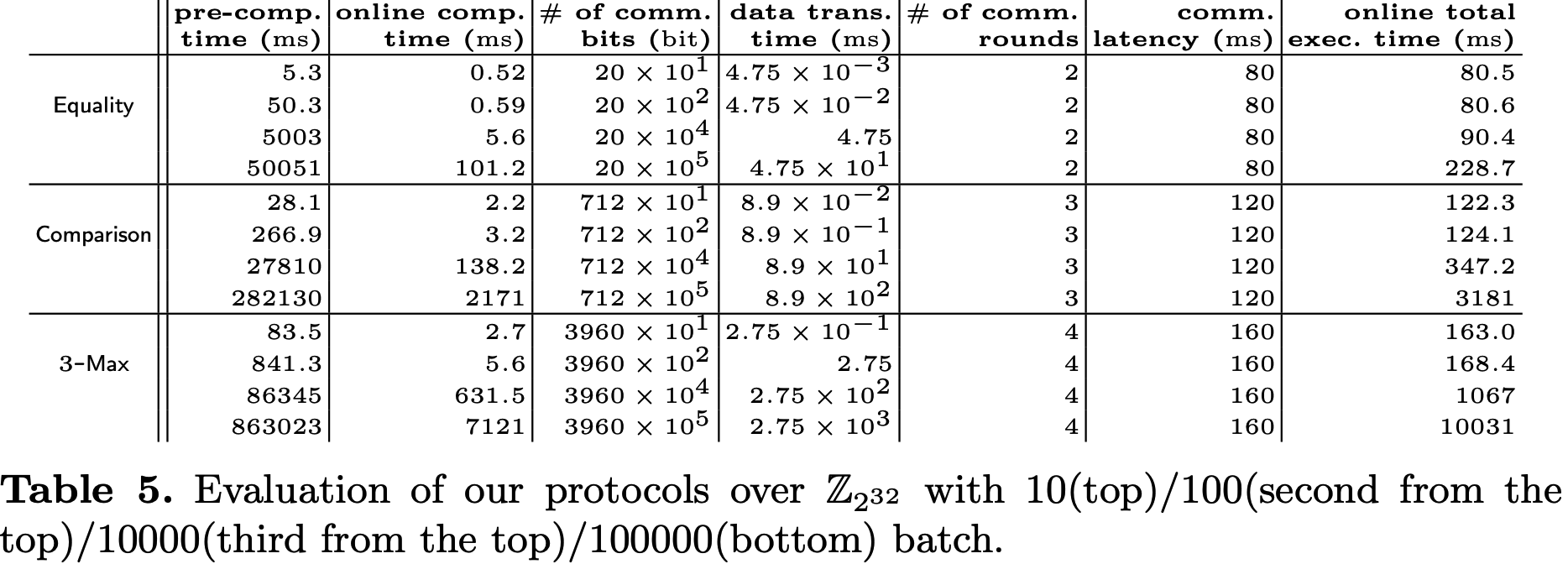
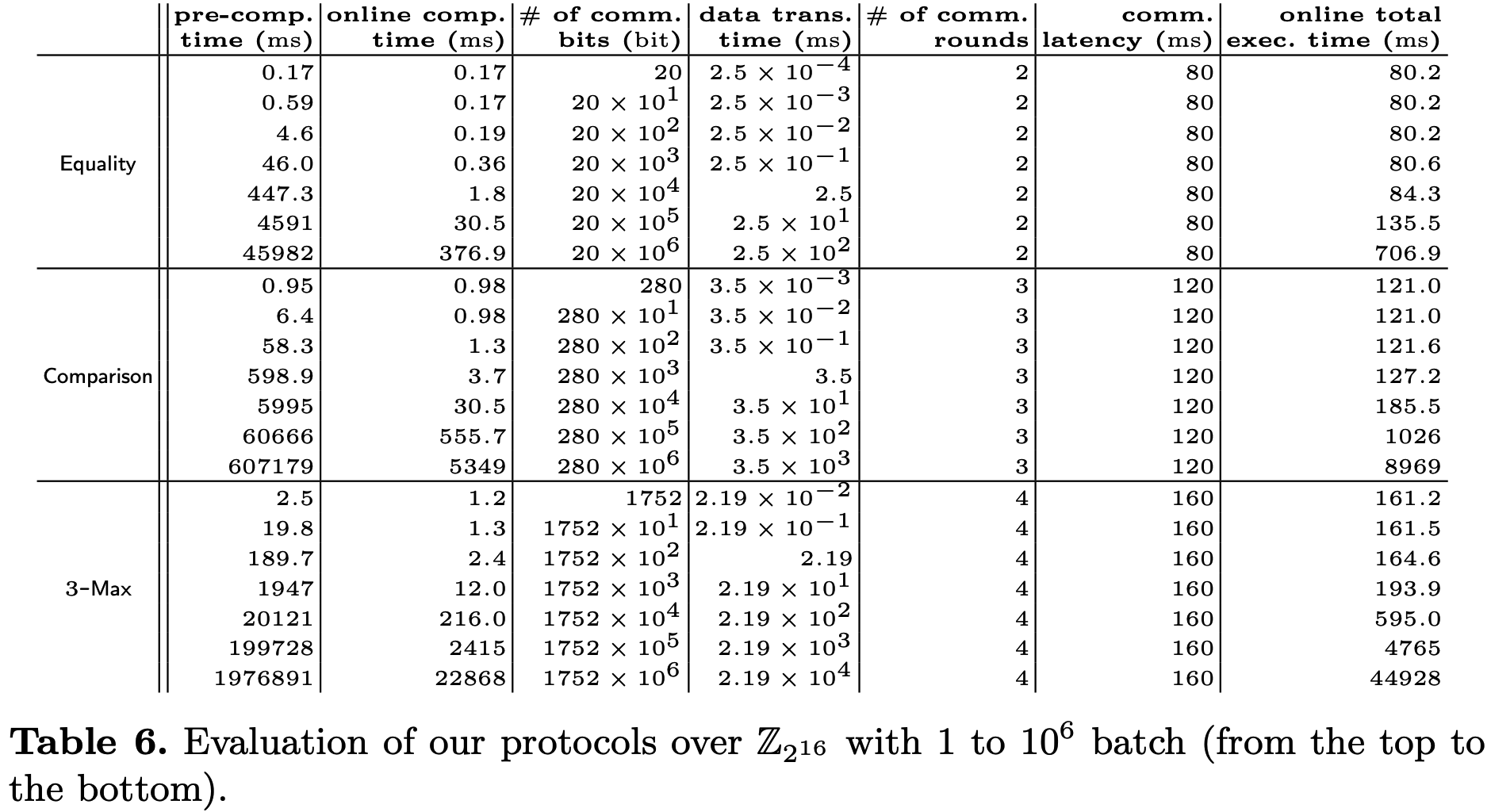
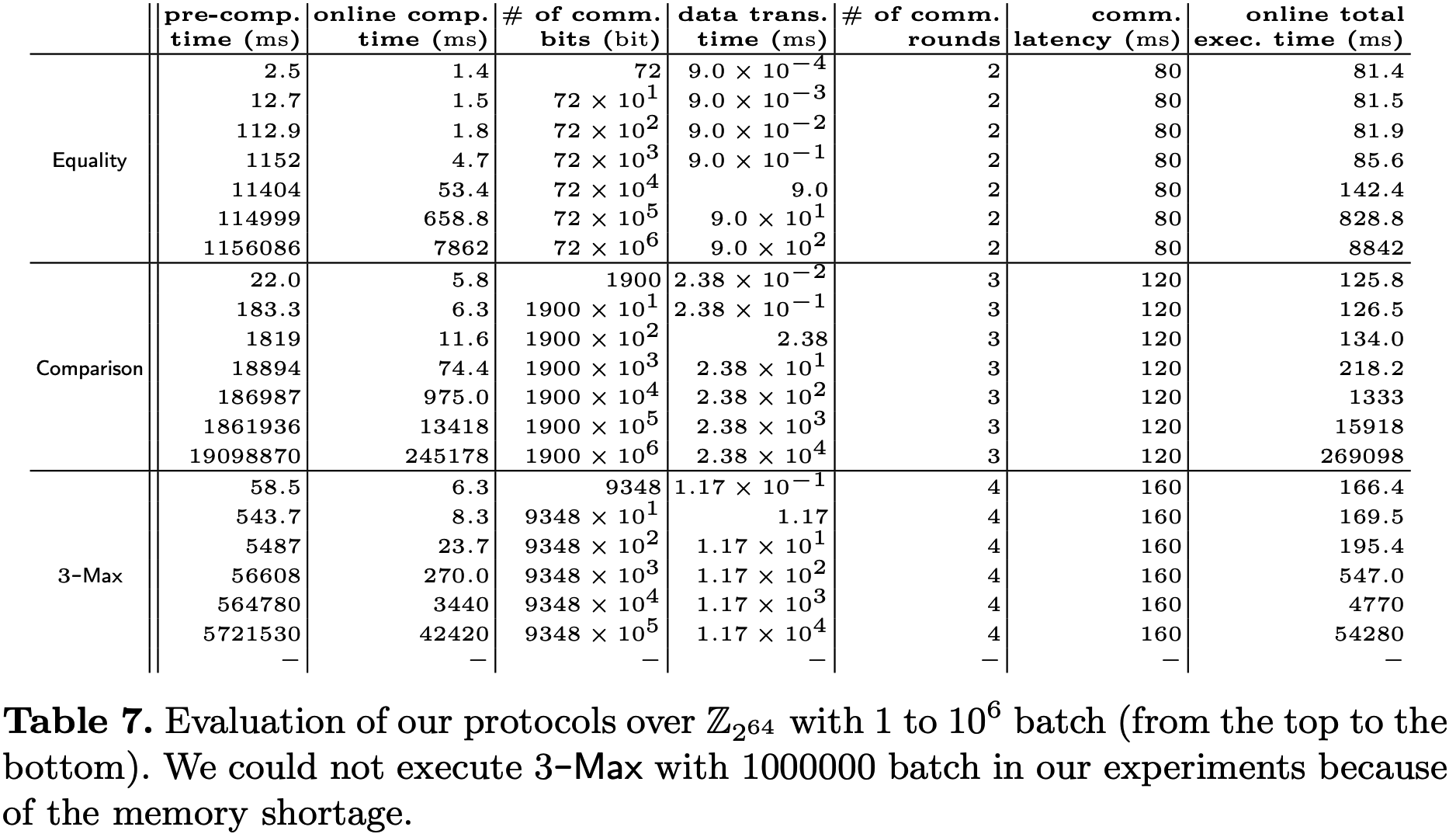
Application: Privacy-Preserving (Exact) Edit Distance

本文还研究了求解隐私基因编辑精确距离方面的应用. 对于两个长度为$L$的基因串$S_0$和$S_1$, 对于动态规划矩阵, 定义每个元素$x[i][j]$为

\[x[i][j]=3\text{-}\mathsf{Min}(x[i-1][j]+1,x[i][j-1]+1,x[i-1][j-1]+e), \]

其中$e=0$当且仅当$S_0[i]=S_1[j]$, 否则$e=1$. 可通过2轮的$\mathsf{Equality}$和1轮的$\mathsf{B2A}$来计算$e$. 为减少总在线执行时间, 可以进行如下优化:

为减少总通信轮次, 并行计算$e$并提前存储, 从而避免每次填充矩阵时计算$e$, 如此只需3轮通信.
矩阵的对角线元素相互独立, 可以对每个$d$并行计算$x[d][0]$, $x[d-1][1]$, $\cdots$, $x[0][d]$来减少通信轮次.

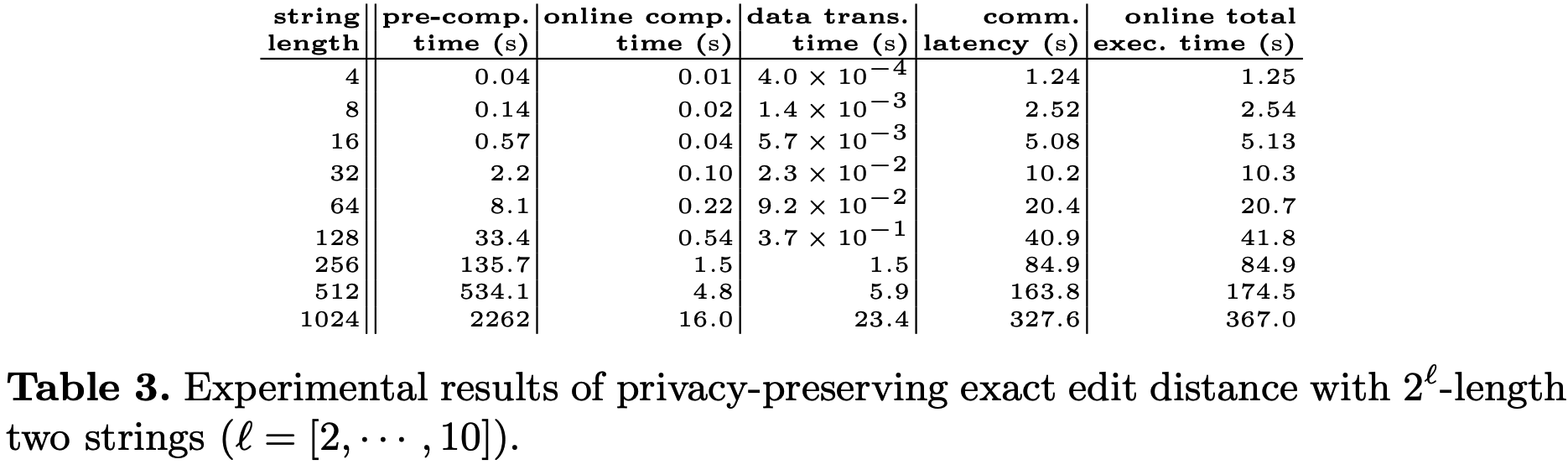
应用以上两个技巧, 计算长度为$L$的基因串的精确编辑距离所需的通信轮次为$3+4(2L-1)=(8L-1)$.

实验结果如下, 可以看到在线总执行时间由通信延迟所主导. 在WAN环境中, 基于GC的方法可能比基于SS的方法快得多, 但如果想要计算多个基因串之间的编辑距离, 例如客户端有1个基因串, 想计算它与服务器上的1000个基因串之间的编辑距离, 则SS-MPC比GC要快得多.

Conclusions

本文通过$N$-BTE来减少基于SS的MPC协议的通信轮次以适应WAN环境, 核心技术是基于Beaver三元组扩展, 但是, 协议所需的计算成本和内存成本与$N$呈指数增长, 因此不适合大批次计算和高延迟网络, 需要在实际应用中对其进行限制.

References

[1] Bogdanov, D., Niitsoo, M., Toft, T., Willemson, J.: High-performance secure multiparty computation for data mining applications. Int. J. Inf. Sec. 11(6), 403–418 (2012).

本文标题: Communication-Efficient (Client-Aided) Secure Two-Party Protocols and Its Application
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16629065662036.html
本站文章采用知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间: 2022-09-11T22:29:26+08:00