ABY3: A Mixed Protocol Framework for Machine Learning
框架概览
ABY3是由 Payman Mohassel 和 Peter Rindal 发表于CCS'18的一项工作,它基于Araki等人提出的三方复制秘密共享(Replicated Secret Sharing,RSS)提出了一种混合计算框架,并且支持Semi-honest和Malicious两种常见的安全模型,非常适合安全外包计算。由于RSS的高效性以及ABY3支持 Arithmetic / Binary / Yao 不同份额之间的相互转换,使其成为目前三方计算下进行安全训练和推理的主流方案之一,主要面向PPML中线性回归、逻辑回归和神经网络。以下主要介绍ABY3在Semi-honest安全模型下的部分协议。
主要贡献
-
三方下的定点截断:SecureML中的本地截断方案在三方下不适用,本文对此进行了改进,并提出了另一种基于截断对(truncation pair)的定点截断方案,此方案可以推广到多方计算中,常见于诚实大多数协议。
-
内积计算的通信开销与向量长度无关:对于长度为\(n\)的两个向量进行内积计算,通常的做法是分开计算\(n \)次定点乘法截断再求和,如此消耗\(n\)个截断对,通信量 \(O(n)\),本文基于RSS的特性提出了改进方案,使得内积计算只需1个截断对,同时通信量变为 \(O(1) \)。
-
Arithmetic / Binary / Yao shares之间的相互转换
-
基于分段多项式的激活函数近似计算
主要协议
设秘密\(x\)的RSS形式为\([\![ x]\!]=(x_1,x_2,x_3)\),其中\(P_i\)的份额表示为\((x_i,x_{(i~\bmod~{3})+1})\),\(i\in\{1,2,3\}\)。基本算子参考原文,这里不做介绍。 \(\newcommand{\RSS}[1]{[\![ #1 ]\!]}\)
三方定点截断
定点数乘法计算后需要进行截断,SecureML中的本地截断方案不能用于3PC中,可转化为2PC下来做,即ABY3中的第一种截断方案。下面只介绍第二种。
对于要进行截断\(d\)位的份额\(\RSS{x'}\), 基本步骤是先计算3-out-of-3 Additive sharing,再转化为2-out-of-3 Replicated sharing。ABY3将这两个步骤进行合并,从而减少一轮在线通信。步骤如下:
预处理:生成随机数的截断对份额\((\RSS{r'},\RSS{r})\),其中\(r=r'/2^d\)。
在线:
- 计算\(\RSS{x'-r'}\)并打开\(x'-r'\);
- 本地计算\(\RSS{x}=(x'-r')/2^d+\RSS{r}\)。
这种截断方案在最低位至多存在1比特误差。
内积计算
内积计算作为机器学习中常见运算之一,构造通信与长度无关的内积计算协议至关重要,此外,矩阵乘法计算也可以转化为内积计算。给定长度为\(n\)的两个向量\(\RSS{\vec{x}}\),\(\RSS{\vec{y}}\),计算\(\RSS{\vec{x}\cdot\vec{y}}=\sum_{i=1}^n\RSS{x_i}\RSS{y_i}\),这里的\(x_i\)表示向量\(\vec{x}\)的第\(i\)个分量。如果将\(n\)个乘法分开计算则需要通信\(n\)次,通信量\(O(n)\),ABY3优化为如下过程:
\[[\![{\vec x}]\!]\cdot[\![{\vec y}]\!]:=\mathsf{reveal}((\sum_{i=1}^n[\![{x_i}]\!]\cdot[\![{y_i}]\!])+[\![{r'}]\!])/2^d-[\![{r}]\!] \]简而言之,是将所有乘法项计算结果求和,通过随机数茫化并打开,最后减掉随机数份额。如此只需通信\(1\)次,通信量\(O(1)\),效率提升了\(n\)倍。此外,由于只截断了一次,因此相比分开截断,ABY3的做法更精确。
A/B/Y shares的相互转换
-
A2B比特分解(bit decomposition):给定\(\RSS{x}^A\),计算\(\RSS{\vec{x}}^B\),满足\(x=\sum_{i=0}^{k-1}2^i\cdot x[i]\),其中\(x[i]\in\{0,1\}\)是\(\vec{x}\)的第\(i\)分量。思路是先将\(\RSS{x}^A=(x_1,x_2,x_3)\)作为3PC的布尔加法电路输入计算和,电路结果即为所求。ABY3中基于FA和PPA对电路进行了优化,使得通信轮次降为\(1+\log k\)。
-
比特提取(bit extraction):给定\(\RSS{x}^A\),计算其第\(i\)位的布尔份额\(\RSS{x[i]}^B\)。思路同上,通过删掉与第\(i\)位无关的电路门来简化电路,如此只需\(O(i)\)个AND门和\(O(\log i)\)轮。
-
B2A比特组合(bit composition):给定\(\RSS{\vec{x}}^B\),计算\(\RSS{x}^A\). 所用的布尔电路与比特分解的相同,只是使用时顺序颠倒。首先\(P_1\)和\(P_2\)输入通过PRF和Nonce生成的随机\(\RSS{-x_2}^B\),同理\(P_2\)和\(P_3\)输入\(\RSS{-x_3}^B\)。然后通过FA计算\(\mathsf{FA}(\RSS{x}^B,\RSS{-x_2[i]}^B,\RSS{-x_3[i]}^B)\rightarrow(\RSS{c[i]}^B,\RSS{s[i]}^B)\). 并通过PPA计算\(\RSS{x_1}^B:=2\RSS{c}^B+\RSS{s}^B\),最后向\(P_1,P_3\)打开\(x_1\),从而得到\(\RSS{x}^A\). 半诚实下中间的步骤可进一步优化为\(P_2\)输入\((-x_2-x_3)\), 然后利用PPA计算\(\RSS{x_1}^B:=\RSS{x}^B+\RSS{-x_2-x_3}^B\)。总之,需要通信\(1+\log k\)轮,计算\(k+k\log k\)个门。
-
Joint Yao Input:本文引入使用MRZ15方案作为Yao sharing,其中\(P_1\)作为评估方,拥有key \(k_X^x\),\(P_2,P_3\)作为混淆方,拥有\(k_X^0\in\{0,1\}^\kappa\)及全局随机偏移量\(\Delta\in\{0,1\}^\kappa\),定义\(K_X^1=K_X^0\oplus\Delta\)。Joint Yao Input可以让所有参与方生成\(\RSS{x}^Y\), 其中\(x\)是两个参与方所知的比特。分为三种情况:
- 若\(P_1,P_2\)知道\(x\),则\(P_2\)本地生成\(\RSS{x}^Y\)并发给\(P_1\);
- 若\(P_1,P_3\)知道\(x\),则\(P_3\)本地生成\(\RSS{x}^Y\)并发给\(P_1\);
- 若\(P_2,P_3\)知道\(x\),则\(P_2,P_3\)通过共同的随机种子选取\(k_X^x\leftarrow\{0,1\}^\kappa\), 然后定义\(k_X^0:=k_X^x\oplus(x\Delta)\),不需要通信。
-
Y2B:\(P_2,P_3\)取key的最后一位为置换位\(p_X=k_X^0[0]\),\(P_1,P_2\)本地生成随机比特\(r\),\(P_1\)发送\(k_X^x[0]\oplus r=x\oplus p_X\oplus r\)给\(P_3\),定义\(\RSS{x}^B=(x\oplus p_X\oplus r,r,p_X)\)。如此需1轮通信,发送1比特信息。
-
B2Y:通过Joint Yao Input,对\(\RSS{x}^B\)进行Yao sharing,然后通过GC的Free-XOR计算\(\RSS{x}^Y=\RSS{x_1}^Y\oplus\RSS{x_2}^Y\oplus\RSS{x_3}^Y\). 半诚实下可进一步优化,\(P_2\)可以计算\(x_2\oplus x_3\),发送\(\RSS{x_2\oplus x_3}^Y\)给\(P_1\),\(P_1\)再本地计算\(\RSS{x}^Y:=\RSS{x_1}^Y\oplus\RSS{x_2\oplus x_3}^Y\)。
-
Y2A:首先\(P_1,P_2\)采样\(x_2\leftarrow\mathbb{Z}_{2^k}\),\(P_2,P_3\)采样\(x_3\leftarrow\mathbb{Z}_{2^k}\),然后使用GC计算\(\RSS{x_1}^Y:=\RSS{x}^Y-\RSS{x_2}^Y-\RSS{x_3}^Y\),最后\(P_1,P_3\)打开\(x_1\),得到\(\RSS{x}^A=(x_1,x_2,x_3)\)。半诚实下可进一步优化,\(P_2\)本地计算\(x_2+x_3\)作为GC的输入,然后计算\(\RSS{x}^Y:=\RSS{x}^Y-\RSS{x_2+x_3}^Y\)。
-
A2Y:通过Joint Yao Input,将\(\RSS{x_i}^A\)转化为\(\RSS{x_i}^Y\),最后用GC计算\(\RSS{x}^Y=\RSS{x_1}^Y+\RSS{x_2}^Y+\RSS{x_3}^Y\)。在半诚实下可进一步优化,\(P_2\)本地计算\(x_2+x_3\)并生成\(\RSS{x_2+x_3}^Y\)发送给\(P_1\),\(P_1\)本地计算\(\RSS{x}^Y:=\RSS{x_1}^Y+\RSS{x_2+x_3}^Y\)。
-
比特映射(bit Injection):计算\(\RSS{a}^A\RSS{b}^B=\RSS{ab}^A\),除使用上面的方案外,还可以进一步优化,可用于计算非线性激活函数。在半诚实模型下,
-
首先构造三方OT协议,三方分别为Sender,Receiver,Helper,其中Helper已知Receiver的选择比特\(c\),定义三方OT的功能为\(((m_0,m_1),c,c)\rightarrow(\perp,m_c,\perp)\),协议过程如下:
- Sender和Helper随机生成\(w_0,w_1\leftarrow\{0,1\}^\kappa\);
- Sender发送\(m_0\oplus w_0\),\(m_1\oplus w_1\)给Receiver;
- Helper发送\(w_c\)给Receiver,则后者可以计算\(m_c=(m_c\oplus w_c)\oplus w_c\)。
-
然后考虑计算\(a\RSS{b}^B=\RSS{ab}^A\),其中\(a\in\mathbb{Z}_{2^k}\)是公开值,\(b\in\{0,1\}\),计算过程如下:
- \(P_1\)和\(P_3\)本地采样\(c_1\leftarrow\mathbb{Z}_{2^k}\),\(P_2\)和\(P_3\)本地采样\(c_3\leftarrow\mathbb{Z}_{2^k}\);
- \(P_3\)作为Sender,定义两个消息\(m_i:=(i\oplus b_1\oplus b_3)a-c_1-c_3\),其中\(i\in\{0,1\}\);
- \(P_2\)作为Receiver,选择比特为\(b_2\);
- \(P_1\)作为Helper,已知\(b_2\),通过三方OT协议,将掩码发给\(P_2\);
- \(P_2\)计算\(c_2=m_{b_2}=(b_2\oplus b_1\oplus b_3)a-c_1-c_3=ba-c_1-c_3\);
- \(P_2\)将\(c_2\)发给\(P_1\),以保持2-out-of-3 RSS语义。
以上需要2轮通信,\(4k\)比特的通信量。为减少通信轮数,可并行一次三方OT,\(P_3\)作为Sender发送\(m_0,m_1\),而\(P_1\)作为Receiver输入\({b_2}\),从而在1轮中让\(P_1\)得到\(m_{b_2}=c_2\),如此需要\(6k\)比特通信量。
-
最后,计算\(\RSS{a}^A\RSS{b}^B=\RSS{ab}^A\),可分解为\(\RSS{a}^A\RSS{b}^B=(a_1+a_2+a_3)\RSS{b}^B=a_1\RSS{b}^B+(a_2+a_3)\RSS{b}^B\)。因此调用两次上面协议来计算,其中第一项由\(P_1\)作为Sender,第二项由\(P_3\)作为Sender。如此每方通信1轮,\(4k\)比特的通信量。
-
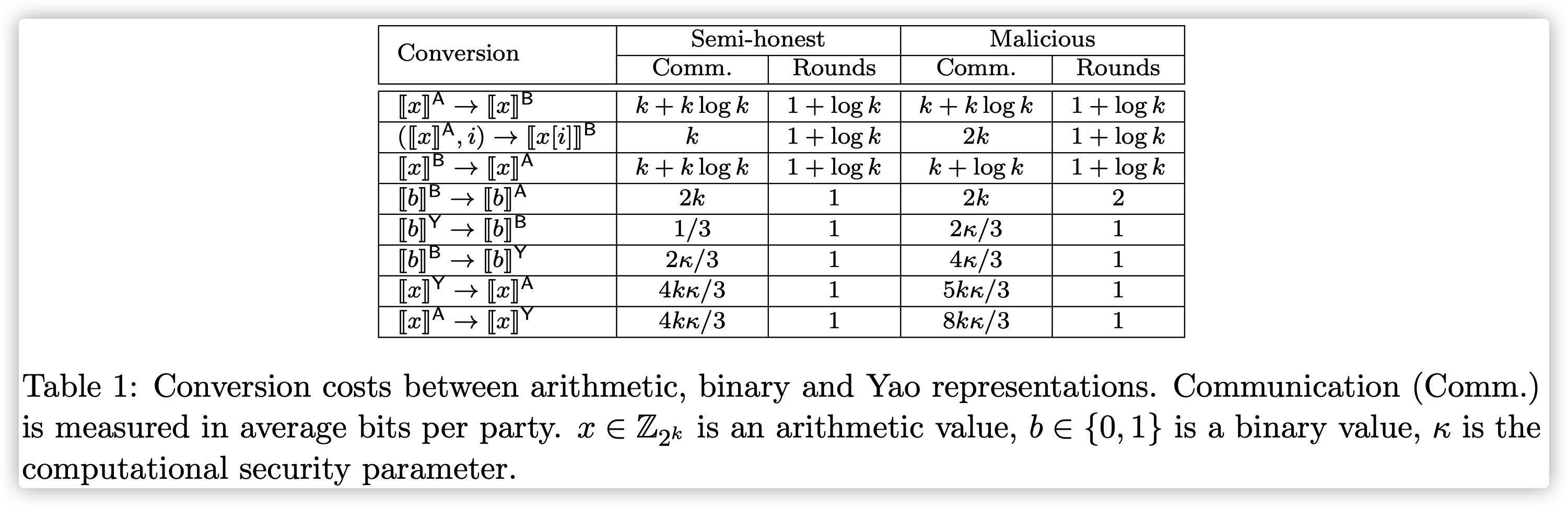
不同转换协议的理论开销如下:
非线性激活函数的近似计算
ABY3中基于\(a[\![ b]\!]^B=[\![ ab]\!]^A\)和\([\![ a]\!]^A[\![ b]\!]^B=[\![ ab]\!]^A\),通过分段多项式来近似计算非线性激活函数。
令\(f_1,\cdots,f_m\)是系数公开的多项式, 且\(-\infty=c_0<c_1<\dots<c_{m-1}<c_m=\infty\), 使得
\[f(x)=\begin{aligned} \begin{cases} f_1(x), & x<c_1\\ f_2(x), & c_1\leq x<c_2\\ \cdots\\ f_m(x), &c_{m-1}\leq x \end{cases} \end{aligned} \]为计算\(f\),首先计算秘密分享的向量\(b_1,\cdots,b_m\in\{0,1\}\),满足\(b_i=1\Leftrightarrow c_{i-1}<x\leq c_i\)。则\(f\)可以表示成: \(f(x)=\sum_ib_if_i(x)\)。因此需要通过bit extraction提取符号位或者比较混淆电路来判断\(x\)所在区间。
- 若使用bit extraction,则需要\(O(\log k)\)轮交互,\(O(k)\)比特通信量;
- 若使用比较混淆电路,则只需\(1\)轮交互,但通信量变为\(O(k\kappa)\)比特。
对于每个\(f_i\)的计算,\(f_i([\![ x]\!])=a_{i,j}[\![ x]\!]^j+\cdots+a_{i,1}[\![ x]\!]+a_{i,0}\), 其中\(a_{i,l}\)是公开常数。当多项式次数\(j=0\)时,计算\(b_if_i([\![ x]\!])\)的计算可优化为计算\(a_{i,0}[\![ b_i]\!]^B\)。当\(f_i\)系数是整数时,可以本地计算\([\![ x]\!]^l,a_{i,l}[\![ x]\!]^l\)。当\(f_i\)系数是非零小数时,需要先进行截断。给定\([\![ x]\!]\),只需计算一次\([\![ x]\!]^j,\cdots,[\![ x]\!]^2\),用于\(f_1,\cdots,f_m\),这部分计算可以与\(b_1,\cdots,b_m\)的计算并行。
常见的非线性激活函数计算方式如下:
-
ReLU激活函数:\(f(v)=\begin{cases} 0,& v<0\\ v, &0\leq v \end{cases}\)
-
Sigmoid激活函数的近似计算与SecureML相同,\(f(v)=\begin{cases}0,& v<-1/2\\ v+1/2,&-1/2\leq v\leq 1/2\\ 1,&1/2<v \end{cases}\)
逻辑回归
逻辑回归的安全训练关键在于每轮更新权重如下:
\[\mathbf{w}:=\mathbf{w}-\alpha\frac{1}{\beta}\mathbf X_j^T\times(f(\mathbf{X}_j\times\mathbf w)-\mathbf{Y}_j) \]其中,\(f\)是Sigmoid函数的分段函数近似。
若进行安全预测,则只需计算\(f(\mathbf{X}\times \mathbf w)\);若进行安全训练,参考SecureML的相关步骤,具体算法总结如下:
预处理阶段:
- 生成所需的截断对;
在线阶段:对\(j=1\rightarrow T\), 计算
- 随机选取\(\beta\)个小批量样本\((\mathbf{X}_j,\mathbf{Y}_j)\);
- 调用内积计算协议计算\(\mathbf{U}=\mathbf{X}_j\times\mathbf{w}\)的每个分量;
- 对\(\mathbf{U}\)的每个分量\(u\)调用Sigmoid近似计算协议计算\(z=f(u)\);
- 本地计算\(\mathbf{\Delta}_j=\mathbf{Z}_j-\mathbf{Y}_j\);
- 调用内积计算协议计算\(\mathbf{D}_j=\mathbf X_j^T\times\mathbf{\Delta}_j\);
- 本地计算\(\mathbf{w}_j:=\mathbf{w}_j-\alpha\frac{1}{\beta}\mathbf{D}_j\).
下面是本文的方案和SecureML在逻辑回归方面的对比,可以看到LAN下ABY3的方案计算效率提升非常明显,但WAN下由于交互轮数增多,所以在线阶段与基于GC的SecureML相比不明显,但随着Batch sizes的增加,ABY3的方案几乎没有变化,而SecureML效率降低明显,吞吐量大概相差3x到300x。若考虑并行,则在LAN和WAN设定下能显著提高ABY3协议的吞吐量。
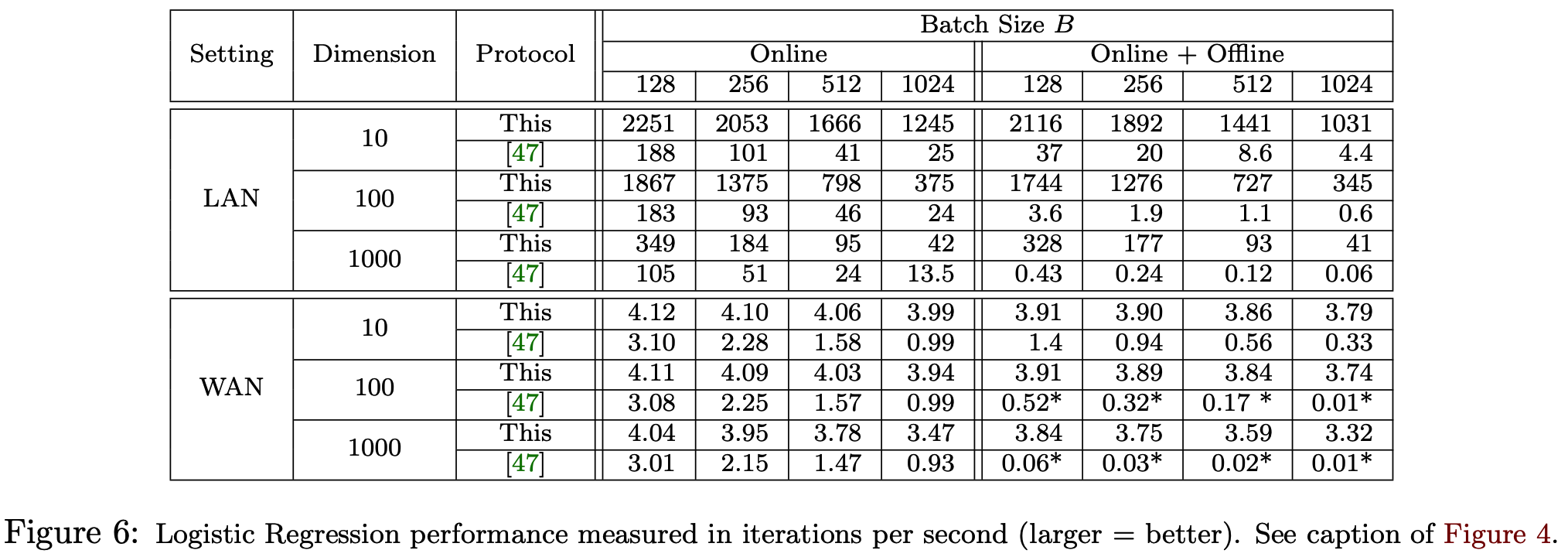
参考文献
[1] P. Mohassel and P. Rindal, “ABY3: A mixed protocol framework for machine learning,” in ACM CCS 2018, D. Lie, M. Mannan, M. Backes, and X. Wang, Eds. ACM Press, Oct. 2018, pp. 35–52.
[2] P. Mohassel, M. Rosulek, and Y. Zhang. Fast and secure three-party computation: The garbled circuit approach. pages 591–602. 2015.
[3] P. Mohassel and Y. Zhang. Secureml: A system for scalable privacy-preserving machine learning. In 2017 IEEE Symposium on Security and Privacy, SP 2017, San Jose, CA, USA, May 22-26, 2017, pages 19–38. IEEE Computer Society, 2017.
本文标题: ABY3: A Mixed Protocol Framework for Machine Learning
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16562245505906.html
本站文章采用 知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间: 2022-06-26T14:22:30+08:00