Tetrad: Actively Secure 4PC for Secure Training and Inference

今天给大家带来的是发表于NDSS'22上的一篇文章 Tetrad: Actively Secure 4PC for Secure Training and Inference, 原文链接: https://arxiv.org/pdf/2106.02850.pdf

Abstract

本文在诚实大多数假设下提出了一个环上抵抗1个恶意敌手的四方计算框架Tetrad, 所提出的两种变体Tetrad, Tetrad-R可以分别达到公平性(Fairness)和输出可达性(Guaranteed output delivery, GOD)/鲁棒性(Robustness). Tetard通过改进Trident的方案实现Fairness, 实现Fairness的乘法协议只需通信5个环元素. 而Tetrad-R实现GOD几乎是免费的, 通过改进SWIFT和Fantastic Four的方案实现GOD. 这两种变体的其他亮点有: (a)无开销的概率截断; (b)多输入乘法协议; (c)通过专用的混淆电路, 支持算术/布尔计算域之间的相互转换, 可同时用于安全训练和安全推理. 实验部分, 在LeNet, VGG16等DNN中进行了性能测试, 发现Tetrad在ML训练速度提高了6倍, 在ML推理中速度提高了5倍. Tetrad在实际部署中所需的货币成本也比Trident低6倍.

Main Contributions

与Trident相比, Tetrad的公平乘法协议只需通信5个环元素(Trident需要6个), 而鲁棒乘法协议的实现在均摊意义下几乎是免费的(在二次幂环$\mathbb Z_{2^{64}}$, 统计安全参数为$40$的情况下, 计算一个包含$2^{20}$个乘法的电路, 平均每个乘法仅需通信0.027bits). Tetrad的其他亮点包括:

通过并行化来支持按需计算, 这在依赖于函数的预处理模型中通常是不可能的;
首次在公平性和输出可达性的前提下实现无开销的概率截断;
可以一个在线通信轮次内计算3输入和4输入的乘法, 与2输入乘法相同, 而以往的方案需要两个轮次;
大多数基于MPC的PPML框架中的大部分计算都在算术世界和布尔世界中完成的, 而混淆世界仅用于在算术/布尔世界中代价高昂的非线性算子的计算(如SoftMax), 然后需要将混淆输出再转换回其他两个世界, 为了进一步优化这个过程, 本文提出了4PC混合协议框架, 可在计算域与专用的基于混淆电路的端到端转换协议, 使混淆世界的输出直接变为其他世界的输出, 从而减少所需的通信量和轮数.

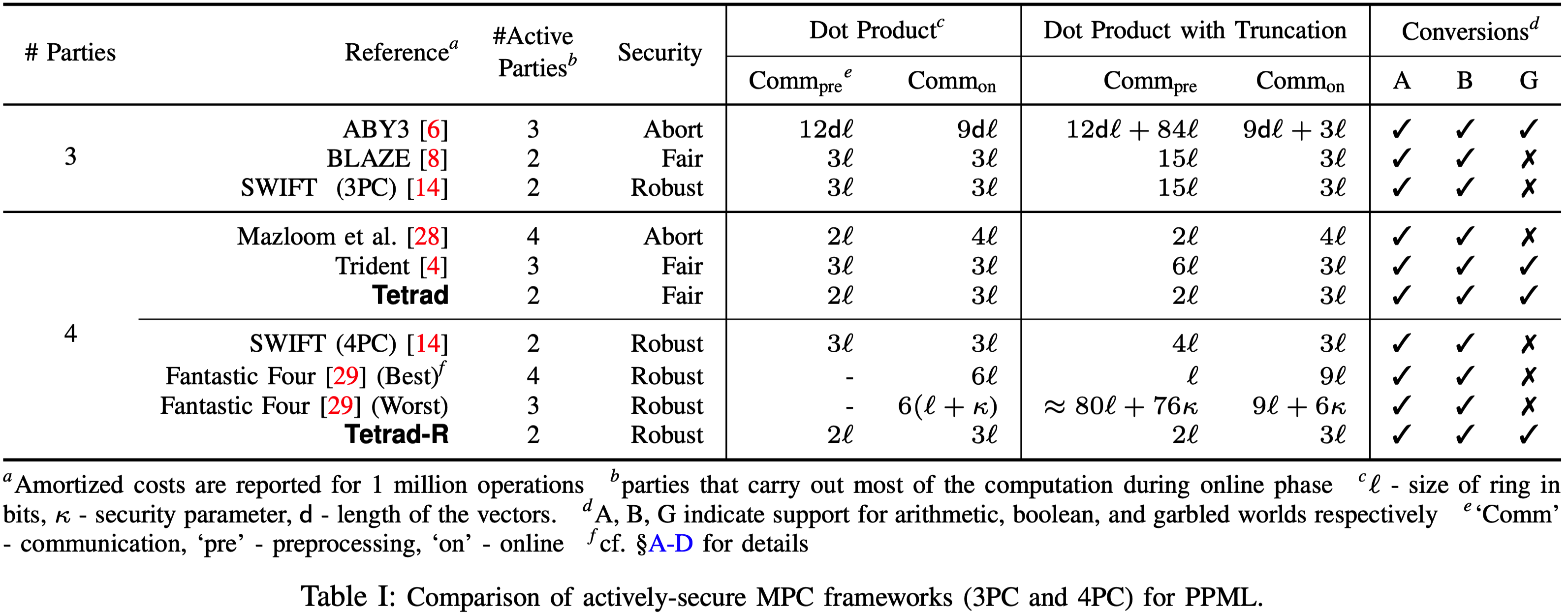
本文与其他现有的3PC, 4PC主动安全的框架对比如下:

Preliminaries and Definitions

服务器代理模式, 四方诚实大多数假设下的安全外包计算, 静态主动敌手至多腐化1个服务器(服务器即为MPC协议的参与方). 参与方之间共享一次分享密钥用于非交互地生成相关随机性.

安全训练: 数据所有者将数据通过秘密共享外包给服务器, 由服务器进行MPC训练模型, 最后向数据所有者重构经过训练的模型.
安全推理: 模型所有者在服务器之间秘密共享一个预先训练的模型, 客户端在服务器之间秘密共享其查询, 服务器通过MPC进行安全推理, 并将输出重构给客户端.

所涉及的计算域为算术环和布尔环$\mathbb Z_{2^{\ell}}=\mathbb Z_{2^{64}}$, $\mathbb Z_2$. 所有浮点数都表示为$\ell=64$比特定点数, 精度$x=13$比特, 整数部分为$\ell-x-1=40$比特.

Sharing Semantics

本文中根据实际参与方的不同, 使用了四种分享语义: 两方下的ASS$[\cdot]$, 三方下的ASS$(\!(\cdot)\!)$, 三方下的RSS$\langle \cdot\rangle$和四方下的RSS+mask$[\![\cdot]\!]$. 秘密$v\in\mathbb Z_{2^\ell}$在$(4,1)$RSS下的其中三个份额$\lambda_v^1,\lambda_v^2,\lambda_v^3$可以在预处理阶段生成, 而第四个份额取决于$v$的值, 因此由在线阶段生成. $\lambda_v=\lambda_v^1+\lambda_v^2+\lambda_v^3$作为掩码, 掩盖值为$m_v=v+\lambda_v$. Tetrad中的$v$的不同秘密共享语义下参与方拥有的份额可表示为下表, 其中$v=v_1+v_2(+v_3)$, $v=m_v+\lambda_v$. 使用的三种中间分享语义$[\cdot],(\!(\cdot)\!),\langle\cdot\rangle$都是线性的, 因此线性算子的安全计算是不需要交互的. 将四方分成两个集合: 计算集合$\mathcal E=\{P_1,P_2\}$, 这里的参与方被分配了计算任务, 在整个在线阶段中都是活动的; 帮助集合$\mathcal D=\{P_0,P_3\}$用于辅助$\mathcal E$进行验证, 只在计算接近尾声的阶段才活动.

	$P_0$	$P_1$	$P_2$	$P_3$
$[\cdot]$-sharing	—	$v^1$	$v^2$	—
$(\!(\cdot)\!)$-sharing	—	$v^1$	$v^2$	$v^3$
$\langle\cdot\rangle$-sharing	—	$(v^1,v^3)$	$(v^2,v^3)$	$(v^1,v^2)$
$[\![\cdot]\!]$-sharing	$(\lambda_v^1,\lambda_v^2,\lambda_v^3)$	$(m_v,\lambda_v^1,\lambda_v^3)$	$(m_v,\lambda_v^2,\lambda_v^3)$	$(m_v,\lambda_v^1,\lambda_v^2)$

一些符号: $\gamma_{a_1\cdots a_n}=\prod_{i=1}^n\lambda_{a_i}, m_{a_1\cdots a_n}=\prod_{i=1}^nm_{a_i}$. $[\![\cdot]\!]^\mathbf B$表示布尔份额, $[\![\cdot]\!]^\mathbf G$表示混淆份额, 没有上标表示算术份额.

4PC Protocol

Primitives

Joint-Send/jsnd: 允许$P_i,P_j$将信息转发给$P_k$进行验证, 当传递的信息不一致时输出$\mathtt{abort}$. 具体做法是, $P_i$发送$v$, $P_j$发送$\mathsf H(v)$, $P_k$使用Hash验证$v$的结果是否为$P_j$发送的信息$\mathsf H(v)$, 若一致则接受, 否则发出中止信号$\mathtt{abort}$. 为均摊开销, Hash的结果可以在协议结束后将信息组合在一起发送一次来均摊通信开销.
Joint-Send for robust protocols: 为实现鲁棒性, Tetrad同时借鉴了Fantastic Four和SWIFT的做法: 当$P_k$发现信息不一致时, 会建立一个至多有两方的参与方集合, 其中必有一个参与方是被敌手腐化的, 这意味着剩下的两方都是诚实的, 因此让其中一方作为TTP($\mathsf P_\mathsf{TP}$)进行相关明文计算. jsnd包含两个阶段: 发送阶段(send)和验证阶段(verify). 验证阶段只在协议结束后执行一次以均摊通信开销. 具体协议过程如下, 均摊的通信开销为$\ell$比特, 2轮.

Sharing: $\Pi_\mathsf{Sh}$协议允许$P_i$生成$v$的$[\![\cdot]\!]$份额. 具体协议见图1, 当参与方发现接收到的信息不一致时, 根据公平性和鲁棒性的要求, 具体处理方式略有不同, 参与方输出$\mathtt{abort}$以实现公平性, 参与方使用一个默认值以实现鲁棒性. 在线阶段均摊通信开销: 至多$3\ell$比特, 1轮.

Joint Sharing: $\Pi_\mathsf{JSh}$协议允许$P_i,P_j$联合生成$v$的$[\![\cdot]\!]$份额, 与$\Pi_\mathsf{Sh}$不同的是, 在线阶段的最后部分需要调用jsnd发送$m_v$给$P_1,P_2,P_3$. 特别地, 若$P_0$与另一方联合生成$v$的$[\![\cdot]\!]$份额, 则可以进一步优化通信, 具体来说,
- $(P_0,P_1)$: $\mathcal P\backslash\{P_2\}$选取$\lambda_v^1\in_R\mathbb Z_{2^\ell}$; 令$\lambda_v^2=m_v=0$; $P_0,P_1$调用jsnd发送$\lambda_v^3=-v-\lambda_v^1$给$P_2$.
- $(P_0,P_2)$: $\mathcal P\backslash\{P_3\}$选取$\lambda_v^3\in_R\mathbb Z_{2^\ell}$; 令$\lambda_v^1=m_v=0$; $P_0,P_2$调用jsnd发送$\lambda_v^2=-v-\lambda_v^3$给$P_3$.
- $(P_0,P_3)$: $\mathcal P\backslash\{P_1\}$选取$\lambda_v^2\in_R\mathbb Z_{2^\ell}$; 令$\lambda_v^3=m_v=0$; $P_0,P_3$调用jsnd发送$\lambda_v^1=-v-\lambda_v^2$给$P_1$.
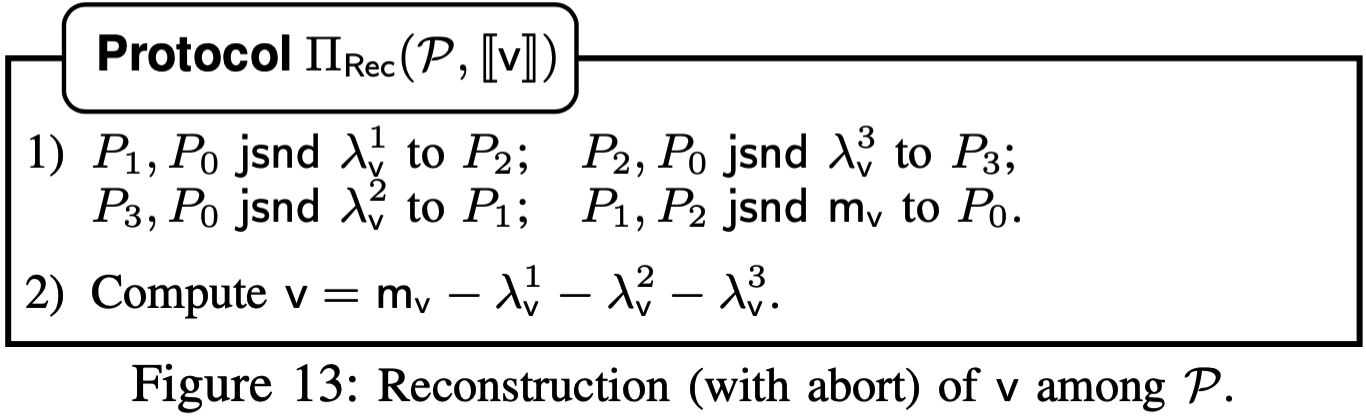
Reconstruction: $\Pi_\mathsf{Rec}$协议输入$[\![v]\!]$, 参与方得到$v$. 因为一个参与方缺失的份额都由其余三方持有, 三方中任意两方通过jsnd发送所需份额即可重构秘密$v$. 具体协议过程如下, 在线阶段均摊通信开销为$4\ell$比特, 1轮.

$\mathcal{F}_\mathsf{zero}$ - 生成0的ASS份额(Zero sharing): 对于$i\in\{1,2,3\}$, 使$P_0,P_i$得到$Z_i$, 满足$Z_1+Z_2+Z_3=0$. 与ABY3一样, 可以通过预分享密钥结合PRF来生成. 对$j\in\{1,2,3\}$, $\mathcal P\backslash\{P_j\}$通过预分享密钥和PRF选取随机$r_j$, 份额定义为$Z_1=r_3-r_2$, $Z_2=r_1-r_3$, $Z_3=r_2-r_1$.
Multiplication $\Pi_\mathsf{MulR}$: 给定$\langle a\rangle,\langle b\rangle$, 生成$\langle z\rangle$, 其中$z=xy$, $P_0$有明文的$a,b$. 原理与ABY3中的RSS乘法一致, 结合zero sharing即可计算, 而resharing则通过调用jsnd来实现. 协议过程如下:

Multiplication in Tetrad

给定$a,b$的份额$[\![a]\!],[\![b]\!]$, 计算$z=ab$的份额$[\![z]\!]$. 协议设计使得$P_0,P_3$在预处理阶段得到$r$的茫化值$r$, $P_1,P_2$在在线阶段得到$z$的茫化值$z-r$, 然后参与方通过执行$\Pi_\mathsf{Jsh}$生成这些值的$[\![\cdot]\!]$份额, 最后本地计算$[\![z-r]\!]+[\![r]\!]$得到输出.

(1) 在线阶段: 因为

\[\begin{aligned} z-r&=ab-r=(m_a-\lambda_a)(m_b-\lambda_b)-r\\ &=m_{ab}-m_a\lambda_b-m_b\lambda_a+\gamma_{ab}-r. \end{aligned}\tag{1} \]

在等式$(1)$中, $P_1,P_2$可以本地计算$m_{ab}$, 关键在于如何计算$y=(z-r)-m_{ab}=-m_a\lambda_{b}-m_b\lambda_a+\gamma_{ab}-r$. 设$y=y_1+y_2+y_3$, 其中$y_1,y_2$由$P_1,P_2$分别计算, 而$y_3$由$P_1,P_2$共同计算如下:

\[\begin{aligned} P_1&:y_1=-\lambda_{a}^1m_b-\lambda_{b}^1m_a+[\gamma_{ab}-r]_1\\ P_2&:y_2=-\lambda_{a}^2m_b-\lambda_{b}^2m_a+[\gamma_{ab}-r]_2\\ P_1,P_2&:y_3=-\lambda_{a}^3m_b-\lambda_{b}^3m_a. \end{aligned}\tag{2} \]

预处理阶段使得$P_1,P_2$收到$\gamma_{ab}-r$的$[\cdot]$份额. $P_1,P_2$互相交换缺失的份额重构$y$, 随后可以重构$z-r$.

(2) 验证阶段: 为了确保在线阶段交换的值的正确性, 为此可以通过$P_3$来辅助验证. 具体而言, 让$P_3$得到$y_1+y_2+s$, 其中$s$是$P_0,P_1,P_2$都已知的随机掩码. 为此, $P_3$需要在预处理阶段得到$\gamma_{xy}+s$. 这里的掩码$s$用于茫化$\gamma_{ab}$防止泄漏给$P_3$. $P_3$计算$\mathcal H(y_1+y_2+s)$并发送给$P_1,P_2$, 若不一致则输出$\mathtt{abort}$.

(3) 预处理阶段: 参与方需要在预处理阶段得到如下值: (i) $P_1,P_2$需得到$[\gamma_{ab}-r]$; (ii) $P_0,P_3$需得到$r$; (iii) $P_3$需得到$\gamma_{ab}+s$.

对于(i)和(ii), 令$\gamma_{ab}=\gamma_{ab}^1+\gamma_{ab}^2+\gamma_{ab}^3$, 其中$P_0$和$P_i$可计算$\gamma_{ab}^i$. 对$P_1,P_2$, 为了组成$(\gamma_{ab}-r)$的加法份额, 定义$\gamma_{ab}-r=\gamma_{ab}^1+\gamma_{ab}^2+[\gamma_{ab}^3-r]$. 此时$P_0,P_3$不随机选取$r$, 而是让$P_0,P_3$先连同$P_j$选取$\gamma_{ab}^3-r$的份额$u^j$, $j\in\{1,2\}$, 然后$P_0,P_3$计算$r=\gamma_{ab}^3-u^1-u^2$. 注意到如此计算的$r$仍是均匀随机的, 因为$u^1,u^2$的选取是均匀随机的.

对于(iii), $P_3$需要得到$w=\gamma_{ab}^1+\gamma_{ab}^2+s$. 为此, $P_0,P_1,P_2$选取$s_1,s_2$, 并设$s=s_1+s_2$. 对$i\in\{1,2\}$, $P_0,P_i$调用jsnd发送$\gamma_{ab}^i+s_i$给$P_3$, 这需要通信2个元素. 作为优化, 可让$P_0$发送$w$给$P_3$. 若$P_0$是恶意的, 则可能发送错误的$w$给$P_3$. 然而, 在这种情况下, 在线阶段$P_1,P_2,P_3$都将是诚实方, 因为$P_1,P_2$在计算中不需要$w$, 而错误的$w$在验证阶段会被发现.

(4) 截断: 设需要截断的值为$z$, 本文中的方法与ABY3的方法类似, 只是在本文的秘密共享语义下无需额外的通信开销. 在ABY3中, 首先预处理阶段生成截断对$(r,r^t)$, 其中$r^t$是随机值$r$截断后的结果. 然后在在线阶段重构$z-r$, 并计算$z^t=(z-r)^t+r^t$. 本文中的处理方式如下: $P_1,P_2$在在线阶段本地截断$(z-r)$, 并生成$[\![(z-r)^t]\!]$. 类似地, $P_0,P_3$在预处理阶段截断$r$并生成$[\![r^t]\!]$. 最后本地计算$[\![z^t]\!]=[\![(z-r)^t]\!]+[\![r^t]\!]$.

(5) 标量积: 本地计算, 给定常数$\alpha$和$[\![v]\!]$, 计算$\alpha v=\beta^1+\beta^2$, 其中$\beta^1=\alpha(m_v-\lambda^3_v)$, $\beta^2=\alpha(-\lambda_v^1-\lambda^2_v)$. 然而, 在定点表示形式下, 输出需要进行截断. 为此, $P_1,P_2$截断$\beta^1$并执行$\Pi_\mathsf{JSh}$, $P_0,P_3$截断$\beta^2$并执行$\Pi_\mathsf{JSh}$即可.

完整的乘法协议过程如下, 实现公平性预处理阶段需要$2\ell$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮. 实现鲁棒性预处理阶段需要$2\ell$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮.

Achieving Fairness

Tetrad实现公平性的思路与Trident相同. 输出重构之前, 需要确保在验证阶段过后所有诚实方都没有中止协议(alive). 为此, 所有参与方维护一个比特(aliveness bit)$b$, 初始化为$b=\mathtt{continue}$. 若验证阶段某个参与方验证失败, 则设定$b=\mathtt{abort}$. 重构的第一轮, 参与方互相交换他们的$b$, 并接受其中占大多数的那个值. 因为仅有一个腐化方, 因此可以保证所有诚实方的$b$都一致. 若$b=\mathtt{continue}$, 则参与方互相交换他们所缺失的份额并接受其中占大多数的那个值. 作为优化, 可让两方发送重构所需的份额, 而第三方发送该份额对应的哈希值检验一致性.

Achieving Robustness

为了将安全性扩展到鲁棒性的Tetrad-R, 需要额外对乘法的预处理阶段进行验证. 此外, 重构协议与实现公平性的类似, 只是不需要再进行aliveness check, 因为恶意行为将导致识别出一个诚实方$P_\mathsf{TP}$进行明文计算.

乘法协议$\Pi_\mathsf{Mult}$修改如下: 首先将$\Pi_\mathsf{JSh}$替换为鲁棒版本, 这确保了传递的信息的正确性, 或者识别出一个参与方集合, 其中一方是腐化方. 接下来, 为了确保预处理阶段$P_0$发送的$w$的正确性, 引入下图4的协议$\Pi_\mathsf{VrfyP0}$. 若该协议失败, 则参与方在预处理阶段识别出一个诚实方$P_\mathsf{TP}$. 最后, 在线阶段若出现$\mathtt{abort}$的情况, 则$P_0$将被认定为$P_\mathsf{TP}$. 因为$P_0$不参与乘法在线阶段的计算, 且预处理阶段的发送的信息可通过$\Pi_\mathsf{VrfyP0}$验证, 因此这样做是安全的.

现在说明在预处理阶段如何验证$P_0$的发送的信息$w$的正确性. 在乘法协议$\Pi_\mathsf{Mult}$中, $P_0$计算并发送$w=\gamma_{ab}^1+\gamma_{ab}^2+s_1+s_2$给$P_3$, 其中$P_0,P_1,P_2$已知明文的$s_1,s_2$. 注意到对$w^1=\gamma_{ab}^1+s_1$和$w^2=\gamma_{ab}^2+s_2$, $w=w^1+w^2$. $P_0$连同$P_1,P_2,P_3$分别拥有$w^1,w^2$和$w$. 所以, 检验$w$的正确性, 可简化为验证$w\overset{?}{=}w^1+w^2$是否成立. 为了对所有$M$个乘法电路门验证这条关系, 即$\{w_j\overset{?}{=}w_j^1+w_j^2\}_{j\in[M]}$, 一种方式是计算随机线性组合并验证总和的关系式. 当在$\mathbb{F}_p$上计算时, 这种方案有$1/|\mathbb F_p|$的错误概率, 其中$|\mathbb F_p|$是$\mathbb F_p$的大小. 然而, 这种方案不能直接在环上进行, 因为环上并非所有的元都有逆元. 具体而言, 恶意行为可通过检验的概率至多为$1/2$. 为了降低恶意行为通过检验的概率, 可将检验重复$\kappa$次, 从而将概率降为$1/2^\kappa$. 作为优化, 可选取$\{0,1\}$的随机组合验证. 如此, 对于一次检验, 参与方只需要使用预分享密钥选取$M$比特的二进制字符串. 完整的验证协议如下:

若在预处理阶段生成了$\mathtt{abort}$信号, 则鲁棒协议还可以进一步优化. 具体来说, 中止信号要么来自jsnd的验证阶段, 要么来自$\Pi_\mathsf{VrfyP0}$的输出. 当检测到恶意行为时, 发现腐化方的方法是: 参与方首先广播他们在密钥设置阶段建立的预分享密钥, 然后重新计算所有预处理数据并验证所传输的数据来找出腐化方. 这里泄漏预分享密钥不会泄漏输入, 因为预处理数据与输入无关. 在找出腐化方后做法与Fantastic Four相同, 将腐化方从计算中剔除, 然后执行半诚实安全的三方计算协议完成计算任务, 实现GOD.

Supporting On-demand Computations

由于按需计算时底层函数是未知的, 因此无法进行预处理. 在Tetrad中, 通过将预处理阶段转移到在线阶段执行来支持按需计算, 同时仍保持相同的通信开销, 此时的在线阶段变为4PC计算. 与上面的$\Pi_\mathsf{Mult}$不同之处在于: 按需计算的乘法协议$\Pi_\mathsf{Mult}^\mathsf{NoPre}$将$\Pi_\mathsf{Mult}$的预处理阶段中的第1-3步直接移到在线阶段, 第4步直接移到验证阶段. 具体协议过程如下,

Mixed Protocol Framework

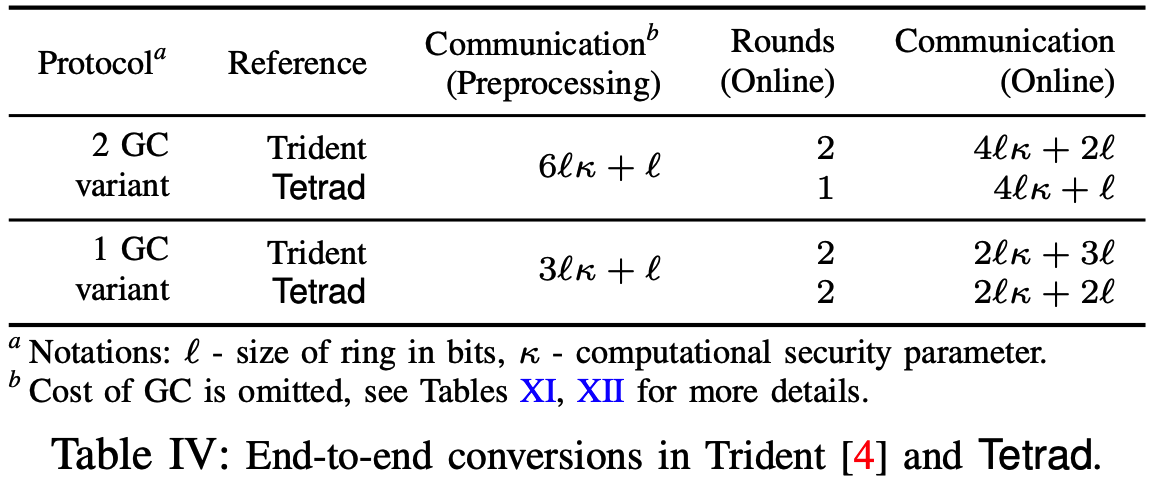
在本文中, 混淆电路被用于对某些函数进行中间评估, 其中函数的输入输出均为$[\![\cdot]\!]$-shared或$[\![\cdot]\!]^\mathbf G$形式. 为此, Tetrad中设计了形式为x-Garbled-x的端到端转换, 其中x可为Arithmetic或者Boolean. 与Trident类似, 本文通过三方混淆电路方案设计了一个实现公平性的混淆世界, 并进一步扩展实现鲁棒性, 而不会增加开销. 利用混淆者诚实占大多数的性质和jsnd, 只需要半诚实的GC计算即可达到主动安全. 本文与Trident相比的结果如下, 端到端转换的在线轮次可以进一步减少到1, 但代价是并行计算中需要再传递一个额外的GC, 记此为2GC变体. 下面分别介绍.

1GC Variant

1GC变体的输入$x=x_1\oplus x_2\oplus x_3$, 其中份额$x_1=m_x\oplus\lambda_x^2$, $x_2=\lambda_x^3$和$x_3=\lambda_x^1$, 定义$[\![x]\!]^\mathbf B$为$m_x$, $\lambda_x^1$, $\lambda_x^2$, $\lambda_x^3$. GC的密钥由三个混淆方$P_0,P_2,P_3$选取, 其中$P_0$, $P_3$生产并通过jsnd发送GC给求值方$P_1$, $P_2$负责辅助密钥传输. 具体来说, $P_0$和$P_3$在混淆之前, 将共同输入$x_3$硬编码到电路中. 如此只需要对输入$x_1,x_2$进行密钥传输. 混淆方$P_0,P_2,P_3$按照与2GC中类似的过程为输入生成密钥, 然后, $P_2,P_3$通过jsnd发送$x_1$给$P_1$, 同时混淆方$P_0,P_2$通过jsnd发送$x_2$的密钥给$P_1$.

评估阶段和输出重构阶段和2GC变体类似, 只是1GC变体仅有一个混淆实例. 在混合协议框架中, 必须向$P_1,P_2$重构输出. 向$P_1$的重构不会产生额外的通信轮次, 因为解码信息的发送可与密钥传输同时进行. 在2GC变体中, 向$P_2$的重构类似于向$P_1$的重构, 而在1GC变体中需要额外通信一轮, 因为$P_2$不再是求值方.

Fairness: 为了实现公平重构协议, 参与方首先需要进行一次aliveness check. 然后按照如下方法重构$z$. 首先, $P_1$发送$q=\mathsf{LSB}(K_z^z)$和$\mathcal H=\mathsf{H}(K_z^z)$给$P_g\in\Phi_1$. 若混淆方从$P_1$处收到了一致的$(q,\mathcal H)$, 满足存在$K\in\{K_z^{0},K_z^{1}\}$, 使得$q=\mathsf{LSB}(K)$, 且$\mathsf{H}(K)=\mathcal H$, 则使用$q$计算$z$, 并发送$z$给与其协作的混淆方. 否则混淆方接受从协作混淆方收到的$z$作为输出. 由此混淆方对输出的进一步传播可以确保所有各方都保持一致. 如果混淆方接收到输出, 则对$P_1$进行$z$的重构. 为此, 所有接收输出的混淆方将解码信息发给$P_1$, $P_1$选择多数值来重构$z$.
GOD: 为实现鲁棒性, 与公平协议的主要不同如下: 首先, 需要使用鲁棒的jsnd. 其次, 在输入共享协议中, 只有混淆方$P_0$有$x_1$, 腐化的$P_0$可能不会向$P_1$提供正确的密钥(作为承诺的打开信息发送). 为了确保达到鲁棒性, 如果$P_1$未能从$P_0$收到正确的密钥, 则让$P_1$发送不一致比特给所有参与方. 所有参与方交换该不一致比特, 并接受其中的多数值. 若所有参与方都确认了存在不一致, 则确定$P_0,P_1$中存在腐化方, 令$P_2$作为TTP进行剩下的计算. 为了确保鲁棒重构, 采用以下方法: 观察到只要$P_1$是诚实的, 公平的重构就提供了鲁棒性. 如果没有混淆方获得公平协议中输出, 则可以确认$P_1$是腐化方, 在这种情况下, 各方选取$P_0$作为TTP进行相关计算并重构输出实现鲁棒性.

2GC Variant

2GC变体有两个并行执行实例, 每个执行包含3个混淆方和1个评估方. 两个独立的执行中$P_1,P_2$分别作为评估方, $\Phi_1=\{P_0,P_2,P_3\}$, $\Phi_2=\{P_0,P_1,P_3\}$分别作为混淆方.

混淆评估分为三个阶段: 输入阶段、评估阶段、输出阶段. 输入阶段为GC的每个输入传输相应的密钥给评估方. 其输入形式为$[\![\cdot]\!]^\mathbf B$份额. 由于在每个混淆实例中函数输入的每个份额都被两个混淆方所持有, 因此可以通过jsnd来确保传输了正确的密钥. 评估阶段包含GC传输和GC评估. 最后在输出阶段, 评估方得到编码输出.

输入阶段: 给定函数输入$x$的秘密份额形式$[\![x]\!]^\mathbf B$, 布尔值$m_x,\alpha_x,\lambda_x^3$, 其中$\alpha_x=\lambda_x^1\oplus\lambda_x^2$和$x=m_x\oplus\alpha_x\oplus\lambda_x^3$, 作为混淆计算的新输入, 为这些值生成$[\![\cdot]\!]^\mathbf{G}$形式的混淆份额. $[\![\cdot]\!]^\mathbf B$的语义确保在每个混淆实例中有两个混淆方持有$(m_x,\alpha_x,\lambda_x^3)$. 面向份额的密钥要么调用jsnd正确地发送给了评估方, 要么检测出不一致. 这种密钥交付实质上为这三个值的每一个生成了$[\![\cdot]\!]^\mathbf G$-sharing, 从而让GC评估. 因此, 输入阶段的目标是对于要通过GC评估的函数的每个输入$x$建立组合份额$[\![x]\!]^\mathbf C=([\![m_x]\!]^\mathbf G,[\![\alpha_x]\!]^\mathbf G,[\![\lambda_x^3]\!]^\mathbf G)$. 下面先讨论$[\![\cdot]\!]^\mathbf G$-sharing的语义, 然后说明生成$[\![\cdot]\!]^\mathbf C$-sharing的步骤.
混淆份额语义: 秘密$v$在$\mathcal P$中是$[\![\cdot]\!]^\mathbf G$-shared, 若$P_i\in\{P_0,P_3\}$拥有$[\![v]\!]_i^\mathbf G=(K_v^{0,1},K_v^{0,2})$, $P_1$拥有$[\![v]\!]_1^\mathbf G=(K_v^{v,1},K_v^{0,2})$, $P_2$拥有$[\![v]\!]_2^\mathbf G=(K_v^{0,1},K_v^{v,2})$. 这里, 对$j\in\{1,2\}$, $K_v^{v,j}=K_v^{0,j}\oplus v\Delta^j$, $\Delta^j$是$\Phi_j$中的混淆方已知的信息, 代表最后一比特为1的全局偏移量且电路中的每根导线都相同. $x\in\mathbb Z_2$被称为$[\![\cdot]\!]^\mathbf C$-shared (compound shared), 若来自$(m_x,\alpha_x,\lambda_x^3)$的每个值, 都通过上述$[\![\cdot]\!]$-shared定义. 记$[\![x]\!]^\mathbf C=([\![m_x]\!]^\mathbf G,[\![\alpha_x]\!]^\mathbf G,[\![\lambda_x^3]\!]^\mathbf G)$.
生成$[\![v]\!]^\mathbf G$和$[\![x]\!]^\mathbf C$: 下图中的协议$\Pi_\mathsf{Sh}^\mathbf G(\mathcal P,v)$可以生成$[\![v]\!]^\mathbf G$, 在每个混淆实例中两个混淆方持有$v$, 处理方式如下: 考虑第一个混淆实例, 评估方为$P_1$, 混淆方$P_k,P_l$持有$v$. $\Phi_1$中的混淆方生成$\{K_v^{b,1}\}_{b\in\{0,1\}}$代表导线$w$上$b$的密钥, 遵循free-XOR技术. $P_k,P_l$调用jsnd发送$K_v^{v,1}$给$P_1$. 第二个混淆的实例类似处理, 最后$\Phi_2$中的混淆方生成$\{K_v^{b,2}\}_{b\in\{0,1\}}$, $P_2$持有$K_v^{v,2}$. 如此, $P_s\in\mathcal P$拥有的$[\![v]\!]_s^\mathbf G$定义为$[\![v]\!]_0^\mathbf G=[\![v]\!]_3^\mathbf G=(K_v^{0,1},K_v^{0,2})$, $[\![v]\!]_1^\mathbf G=(K_v^{v,1},K_v^{0,2})$, $[\![v]\!]_2^\mathbf{G}=(K_v^{0,1},K_v^{v,2})$.

为了生成$[\![x]\!]^\mathbf C$, 给定$[\![x]\!]^\mathbf B$, 需要生成$([\![m_x]\!]^\mathbf G,[\![\alpha_x]\!]^\mathbf G,[\![\lambda_x^3]\!]^\mathbf G)$. 为此, 可以对每个$m_x,\alpha_x,\lambda_x^3$调用$\Pi_\mathsf{Sh}^\mathbf G$.

Evaluation phase

令所要评估的函数为$f(x)$, 函数输入为$[\![\cdot]\!]^\mathbf C$, 即计算$f(m_x,\alpha_x,\lambda_x^3)$. 令$\mathsf{GC}_j$表示$\Phi_j$发送给$P_j\in\{P_1,P_2\}$的混淆电路. 为了减少通信轮次, 在$[\![x]\!]^\mathbf C$生成期间, 发送$\mathsf{GC}_j$的同时也进行密钥传输, 其中$\{P_0,P_3\}$通过jsnd发送$\mathsf{GC}_j$给$P_j$. 在收到$\mathsf{GC}$后, 评估方对相应的混淆电路进行求值得到输出对应的密钥$z$的份额$[\![z]\!]^\mathbf G$.

Output phase

输出阶段的目标是从$[\![z]\!]^\mathbf G$计算并输出$z$. 为了向$P_j\in\{P_1,P_2\}$重构$z$, $\Phi_j$中两个混淆方发送解码信息$p^j=\mathsf{LSB}(K_z^{0,j})$给$P_j$. 若收到的信息一致, 则$P_j$使用收到的$p^j$重构$z=p^j\oplus q^j$, 其中$q^j=\mathsf{LSB}(K_z^{z,j})$; 否则$P_j$中止. 为了向混淆方$P_g\in\{P_0,P_3\}$重构$z$, 评估方$P_1$发送$q^1=\mathsf{LSB}(K_z^{z,1})$和$\mathcal H=\mathsf{H}(K_z^{z,1})$给$P_g$, 其中$\mathsf{H}$是一个抗碰撞哈希函数. 若混淆方从$P_1$收到的$(q^1,\mathcal H)$满足存在$K\in\{K_z^{0,1},K_z^{1,1}\}$, 使得$q^1=\mathsf{LSB}(K)$, 且$\mathsf{H}(K)=\mathcal H$, 则使用$q^1$重构$z=p^1\oplus q^1$; 否则混淆方中止计算. 注意由于混淆方案的可靠性, 腐化的评估方$P_1$不能通过发送并非输出的密钥来欺骗$\{P_0,P_3\}$中的混淆方. 重构是轻量级的, 对于混淆方需要单轮, 而对评估方的重构可以与密钥传输同时进行, 不会产生额外的通信轮次. 具体协议如下:

Optimizations

当部署到混合框架中时, 预处理阶段传输(通信密集的)GC, 并生成独立于输入$x$的$\alpha_x,\lambda_x^3$的$[\![\cdot]\!]^\mathbf{G}$份额. 因此, 在线阶段非常轻量级, 且仅需1轮生成$x$的$[\![\cdot]\!]^\mathbf{G}$份额中的$m_x$. 由于评估是本地计算, 评估方在1轮结束时得到GC输出的$[\![\cdot]\!]^\mathbf G$份额.

Security

Fairness: 首先确认所有参与方都仍在参与协议, 若是, 则按图19中的协议进行公平重构计算, 但主要的不同是: 对于向评估方的重构, 所有三个混淆方发送各自解码信息给评估方. 评估方选择出现最多的值进行重构; 对于向混淆方$P_0,P_3$的重构, 评估方发送输出密钥的最低位及其哈希值给混淆方, 由于至少存在一个评估方是诚实的, 因此混淆方将保持一致.
GOD: 与Fairness最主要的不同是, 使用了鲁棒的jsnd原语来保证当检测到恶意行为时识别出一个诚实方进行相关计算并向所有参与方输出计算结果.

与1GC对比:

Conversions involving Garbled World

假设需用GC计算函数$f$, 输入为$x,y\in\mathbb Z_{2^\ell}$, 输出为$f(x,y)$. 描述的所有转换均适用于2GC变体. 对于Fairness和Robustness变体, 转换是通用的, 其中的安全性来自于底层密码原语的安全性.

Case I: Boolean-Garbled-Boolean. GC的输入为$[\![x]\!]^\mathbf B,[\![y]\!]^\mathbf B$, 参与方调用$\Pi_\mathsf{Sh}^\mathbf G$生成$[\![x]\!]^\mathbf C, [\![y]\!]^\mathbf C$. 此外, 参与方$P_0,P_3$采样$R\in\mathbb Z_{2^\ell}$茫化函数输出$f(x,y)$, 生成$[\![R]\!]^\mathbf B$和$[\![R]\!]^\mathbf G$. 混淆方$P_g\in\{P_0,P_2,P_3\}$混淆计算$z=f(x,y)\oplus R$的电路, 发送GC及其解码信息给评估方$P_1$. 如此也对评估方$P_2$进行类似的步骤. 经过GC评估和输出解码后, 评估方可以得到$z=f(x,y)\oplus R$, 并调用$\Pi_\mathsf{JSh}^\mathbf B$生成$[\![z]\!]^\mathbf B$. 最后参与方计算$[\![f(x,y)]\!]^\mathbf B=[\![z]\!]^\mathbf B\oplus[\![R]\!]^\mathbf B$.
Case II: Boolean-Garbled-Arithmetic. 与Case I类似, 除了电路计算的是$z=f(x,y)+ R$. $z$的布尔份额替换为算术份额$[\![z]\!]$, 最后计算$[\![f(x,y)]\!]=[\![z]\!]-[\![R]\!]$.
Case III & IV: Arithmetic-Garbled-Arithmetic, Arithmetic-Garbled-Boolean. 要计算的函数$f(x,y)$修改为$f'(m_x,\alpha_x,\lambda_x^3,m_y,\alpha_y,\lambda_y^3)=f(m_x-\alpha_x-\lambda_x^3,m_y-\alpha_y-\lambda_y^3)$, 其中输入$x,y$被替换为$\{m_x,\alpha_x,\lambda_x^3\}$, $\{m_y,\alpha_y,\lambda_y^3\}$, $\alpha_x=\lambda_x^1+\lambda_x^2$和$\alpha_y=\lambda_y^1+\lambda_y^2$. 输入的份额可由$\Pi_\mathsf{Sh}^\mathbf G$生成, 其余计算步骤同Case I和Case II, 取决于输出的份额形式.

以上2GC变体转换通信量和通信轮次与Trident的相应方案理论对比:

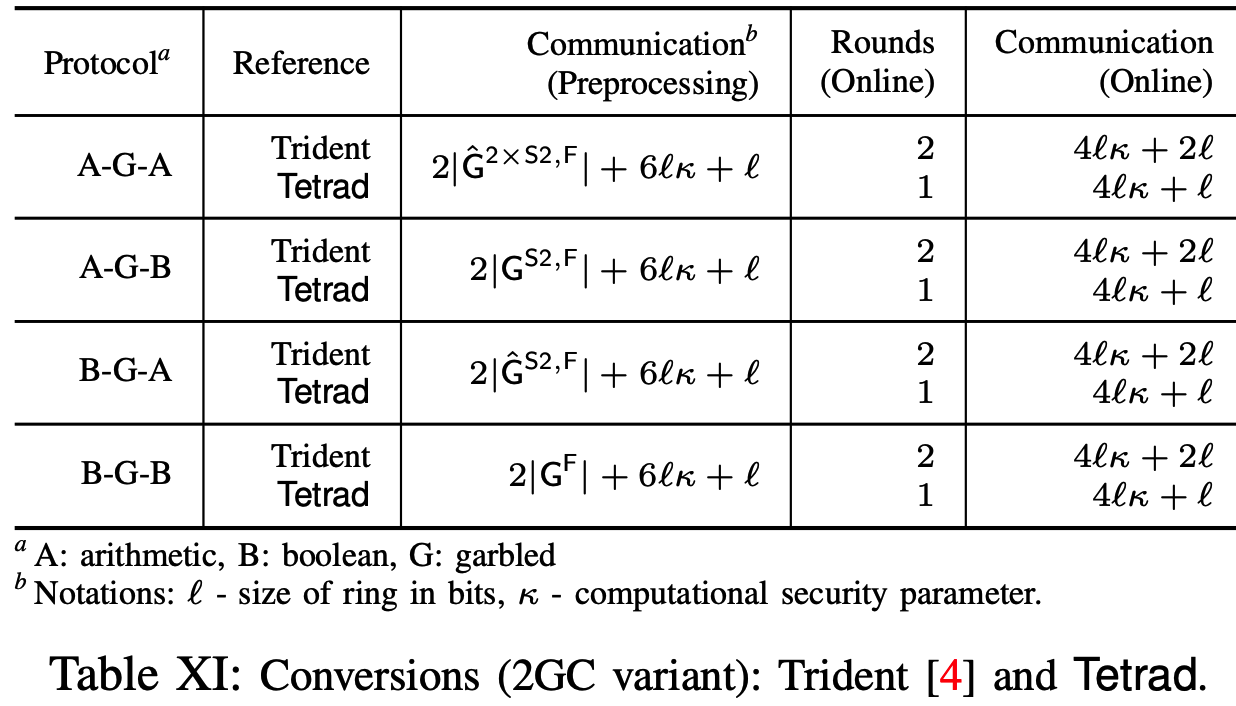
Other Conversions

Arithmetic to Boolean (A2B): $[\![v]\!]\rightarrow[\![v]\!]^\mathbf B$. 因为$v=v_1+v_2$, $P_1,P_2$可计算$v_1=m_v-\lambda_v^3$, $P_0,P_3$可计算$v_2=-(\lambda_v^1+\lambda_v^2)$. 因此, $[\![v]\!]^\mathbf B=[\![v_1]\!]^\mathbf B+[\![v_2]\!]^\mathbf B$, 其中$[\![v_2]\!]^\mathbf B$可在预处理阶段生成, $[\![v_1]\!]^\mathbf B$可在在线阶段通过参与方执行$\Pi_\mathsf{JSh}^\mathbf B$生成. 完整的A2B协议过程如下:

Boolean to Arithmetic (B2A): $[\![v]\!]^\mathbf B\rightarrow[\![v]\!]$. 利用如下关系式 \[v=\sum_{i=0}^{\ell-1}2^iv_i=\sum_{i=0}^{\ell-1}2^i(\lambda_{v_i}\oplus m_{v_i})=\sum_{i=0}^{\ell-1}2^i\left({m_v}_i^\mathsf R+{\lambda_v}_i^\mathsf R(1-2{m_v}_i^\mathsf R)\right). \] 其中, ${\lambda_v}_i^\mathsf R, {m_v}_i^\mathsf R$分别表示环$\mathbb Z_{2^\ell}$上的比特${\lambda_v}_i, {m_v}_i$的算术值. 计算中需要借助$\Pi_\mathsf{bit2A}$协议, 完整的B2A协议过程如下:

Bit to Arithmetic (Bit2A): 给定比特$b$的布尔份额$[\![b]\!]^\mathbf B$, $\Pi_\mathsf{bit2A}$计算其算术份额$[\![b]\!]$. 设$b^\mathsf R$表示$b\in\{0,1\}$在算术环$\mathbb Z_{2^\ell}$的值, 则对于$b=b_1\oplus b_2$, $b^\mathsf R=(b_1^\mathsf R-b_2^\mathsf R)^2$. 令$b_1=m_b\oplus\lambda_v^3$, $b_2=\lambda_v^1\oplus\lambda_v^2$. 为计算$[\![b]\!]$, 可让一对参与方执行$\Pi_\mathsf{JSh}$生成对应于$b_1^\mathsf R$和$b_2^\mathsf R$的算术份额, 然后调用一次$\Pi_\mathsf{Mult}$, 输入$x=y=b_1^\mathsf R-b_2^\mathsf R$来计算$b^\mathsf R$.

可以通过Trident和SWIFT中的方法进一步权衡预处理阶段的通信和计算开销. 计算原理如下:
\[b^\mathsf R=(m_b\oplus\lambda_b)^\mathsf R=m_b^\mathsf R+\lambda_b^\mathsf R-2m_b^\mathsf R\lambda_b^\mathsf R=m_b^\mathsf R+(\lambda_b^\mathsf R)(1-2m_b^\mathsf R) \]
具体协议过程如下, 预处理阶段需要$3\ell+1$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮.

Building Blocks

Dot Product

给定长度为$d$的向量份额$[\![\vec{\mathbf a}]\!],[\![\vec{\mathbf b}]\!]$, $\Pi_\mathsf{dotp}$计算$[\![z]\!]$, 使得$z=(\vec{\mathbf a}\odot\vec{\mathbf b})^t$(截断)或者$z=\vec{\mathbf a}\odot\vec{\mathbf b}$(不截断). 整体思路与SWIFT和Trident类似, 先对$d$个乘法项的部分份额求和, 然后进行一次通信. 此外, 矩阵乘法可以看成点积协议的扩展形式, 卷积计算可以简化为矩阵乘法计算(参考SecureNN), 因此计算方式与之类似. 完整的点积计算协议如下, 预处理阶段需要$2\ell$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮.

Multi-input Multiplication

多输入乘法计算的方法与ABY2.0相同. 例如, 考虑3输入乘法计算, 给定$[\![a]\!],[\![b]\!],[\![c]\!]$, 计算$[\![z]\!]$, 其中$z=abc$. 计算原理与2输入乘法协议类似:

\[\begin{aligned} z-r&=abc-r=(m_a-\lambda_a)(m_b-\lambda_b)(m_c-\lambda_c)-r\\ &=m_{abc}-m_{ac}\lambda_b-m_{bc}\lambda_a-m_{ab}\lambda_c+m_a\gamma_{bc}+m_b\gamma_{ac}+m_c\gamma_{ab}-\gamma_{abc}-r. \end{aligned} \]

类似于2输入乘法公平计算协议(图3), $P_1,P_2$需要在预处理阶段生成交叉项$\gamma_{ab},\gamma_{ac},\gamma_{bc},\gamma_{abc}$的加法份额, 不能本地计算的$\gamma$相关项可由$P_0,P_3$计算并分享给$P_1,P_2$. 与$\Pi_\mathsf{Mult}$相比, 在线阶段的通信量不变, 但预处理阶段的通信量变为9个环元素. 完整的3输入乘法公平计算协议如下, 预处理阶段需要$9\ell$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮. 类似地可以定义4输入乘法计算协议.

Secure Comparison

给定$[\![a]\!],[\![b]\!]$, 比较协议计算$a>b$, 即通过$\Pi_\mathsf{bitext}$抽取$v=a-b$的最高有效位, 然后利用关系$(a>b)=1\oplus\mathsf{MSB}(v)$求解. 而$\Pi_\mathsf{bitext}$有两种方案:

ABY3中通信量优化的Parallel prefix adder (PPA);
ABY2.0中通信轮次优化的比特抽取电路.

由于$v=m_v-\lambda_v=(m_v-\lambda_v^3)+(-\lambda_v^1-\lambda_v^2)$, 在预处理阶段$P_0,P_3$执行$\Pi_\mathsf{JSh}^\mathbf B(-\lambda_v^1-\lambda_v^2)\rightarrow[\![-\lambda_v^1-\lambda_v^2]\!]^\mathbf B$, 在线阶段$P_0,P_3$执行$\Pi_\mathsf{JSh}^\mathbf B(m_v-\lambda_v^3)\rightarrow[\![m_v-\lambda_v^3]\!]^\mathbf B$.

Bit Injection

给定比特$b$的布尔份额$[\![b]\!]^\mathbf B$, $v\in\mathbb Z_{2^\ell}$的算术份额$[\![v]\!]$, $\Pi_\mathsf{bitInj}$计算$[\![bv]\!]$. 类似于$\Pi_\mathsf{bit2A}$, 计算原理如下:

\[\begin{aligned} (bv)^\mathsf R&=(m_b\oplus\lambda_b)^\mathsf R(m_v-\lambda_v)\\ &=(m_b^\mathsf R+(\lambda_b^\mathsf R)(1-2m_b^\mathsf R))(m_v-\lambda_v)\\ &=m_b^\mathsf Rm_v-m_b^\mathsf R\lambda_v+(2m_b^\mathsf R-1)((\lambda_b^\mathsf R)\lambda_v-m_v(\lambda_b^\mathsf R)). \end{aligned} \]

预处理阶段需$6\ell+1$比特通信量, 在线阶段需$3\ell$比特通信量, 1轮.

Oblivious Selection

与不经意传输类似, 给定$[\![x_0]\!]$, $[\![x_1]\!]$和$[\![b]\!]^\mathbf B$, 不经意选取协议$\Pi_\mathsf{obv}$可让参与方生成$z=x_b$的$[\![\cdot]\!]$份额$[\![z]\!]$. 计算原理在于利用关系式$z=b(x_1-x_0)+x_0$, 其中$[\![b(x_1-x_0)]\!]$可以通过$\Pi_\mathsf{bitInj}$来计算.

Piece-wise Polynomial

与ABY3类似, 非线性的激活函数计算可通过分段多项式近似计算, 而分段多项式计算可看成是由一系列常数公开多项式$f_1,\cdots,f_m$和$c_1<\cdots<c_m$组成的, 使得

\[f(y)= \begin{cases} 0,&y<c_1\\ f_1,&c_1\leq y<c_2\\ \cdots\\ f_m,&c_m\leq y \end{cases} \]

则有$f(y)=\sum_{i=1}^mb_i\cdot(f_i-f_{i-1})$, 其中$f_0=0$, $f_m=1$, 对于$i\in\{1,\cdots,m\}$, 若$y\geq c_i$, 则$b_i=1$, 否则$b_i=0$. 因此可以通过安全比较协议和$\Pi_\mathsf{bitInj}$来计算. 在线阶段若对每个$b_i\cdot(f_i-f_{i-1})$调用$\Pi_\mathsf{JSh}$, 则需要调用$m$次, 可以首先计算$f(y)$的加法份额, 然后调用$\Pi_\mathsf{JSh}$一次从而独立于$m$来优化通信. 具体协议过程如下, 预处理阶段需要$m(6\ell+1)$比特通信量, 在线阶段需要$3\ell$比特通信量, 1轮.

ReLU函数: $\mathsf{ReLU}(v)=\begin{cases} 0,& v<0\\ v, &0\leq v \end{cases}$
Sigmoid函数: 与SecureML一致, $\mathsf{Sig}(v)=\begin{cases}0,& v<-1/2\\ v+1/2,&-1/2\leq v\leq 1/2\\ 1,&1/2<v \end{cases}$

ArgMin / ArgMax

给定长度为$m$的向量$\vec{\mathbf x}=(x_1,\cdots,x_m)$的$[\![\cdot]\!]$-sharing, $\Pi_\mathsf{argmin}$计算最小元素所在的索引, 输出长度为$m$的one-hot比特向量$\vec{\mathbf b}$的$[\![\cdot]\!]^\mathbf B$-shared, 其中最小元素所在索引置为1, 其余为0. 本文中使用的是Damgård等人在S&P'19提出的基于二叉树的方法通过分组比较和递归的方式来计算$\vec{\mathbf x}$中的最小元素, 并同时更新$\vec{\mathbf b}$. 首先将$\vec{\mathbf b}$的每个比特都初始化为1. 通过将$\vec{\mathbf x}$的元素进行分组, 逐对进行安全比较得出最小值所在位置, 并更新另一个位置的值为0. 如此递归最后只有整个向量中的最小值所在位置仍为1, 其余为0. 类似的思想可以用于$\Pi_\mathsf{argmax}$求最大值所在的索引. 完整的协议过程如下:

Implementation and Benchmarking

实验部分只针对实现公平性的方案, 不考虑鲁棒性, 因为后者使用了鲁棒的联合发送原语(jsnd)且预处理阶段最后进行一次性验证, 相比前者, 后者开销更小.

实验相关基准含义如下:

ML Training

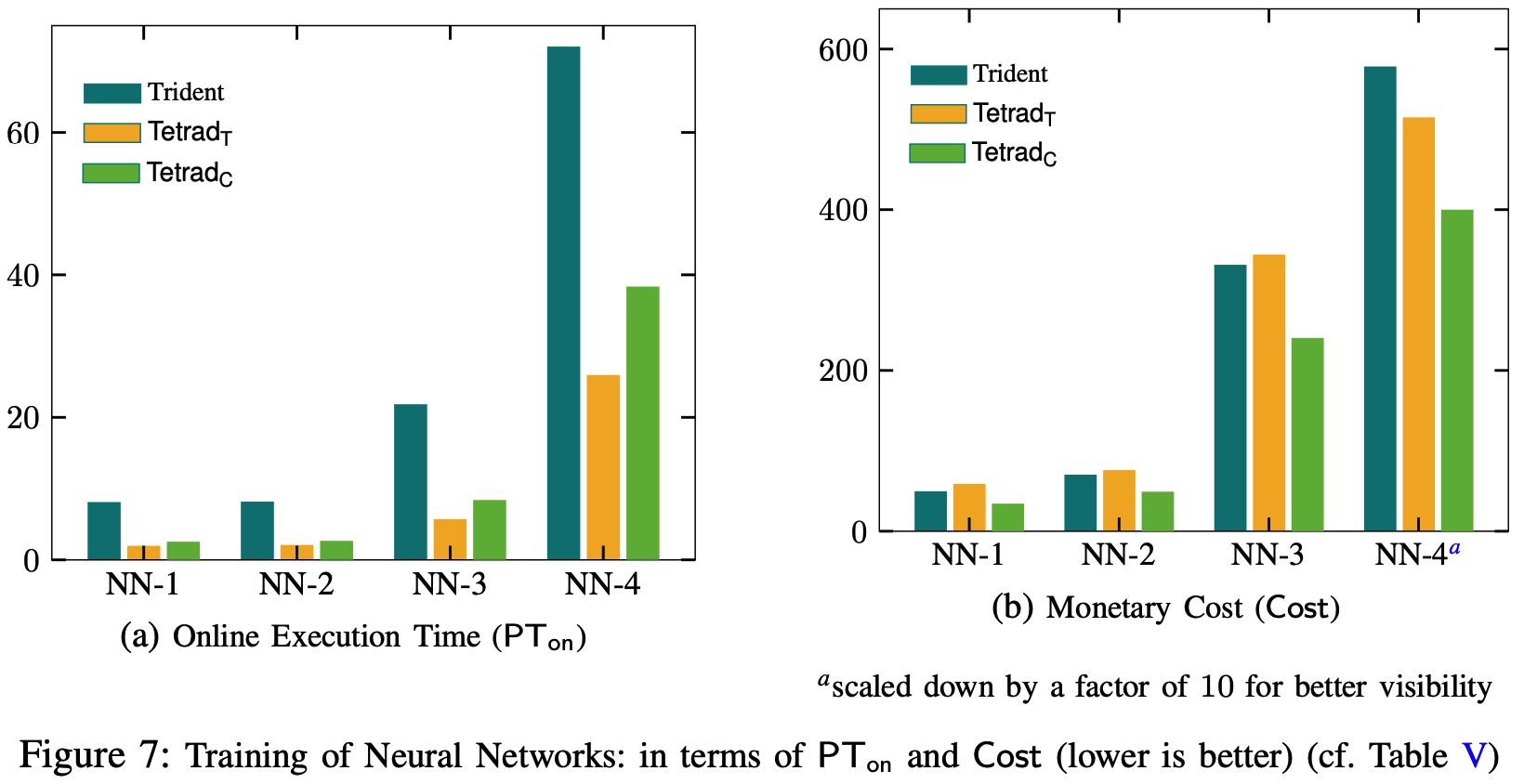
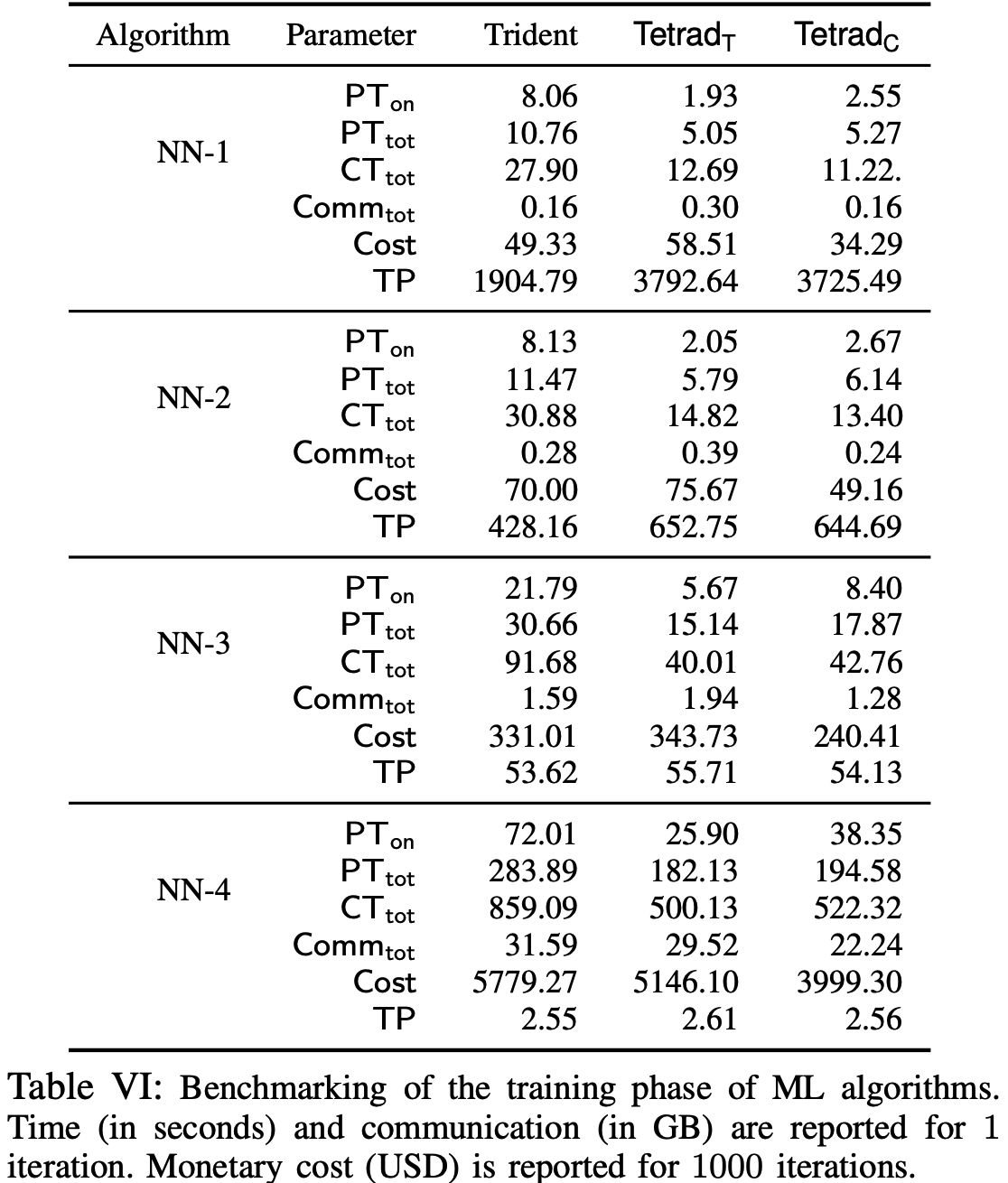
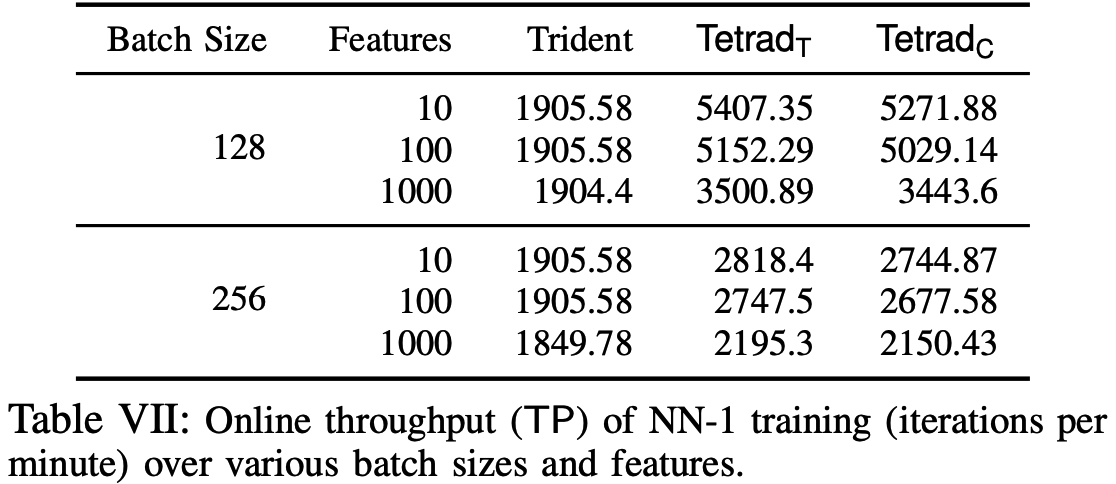
ML Inference

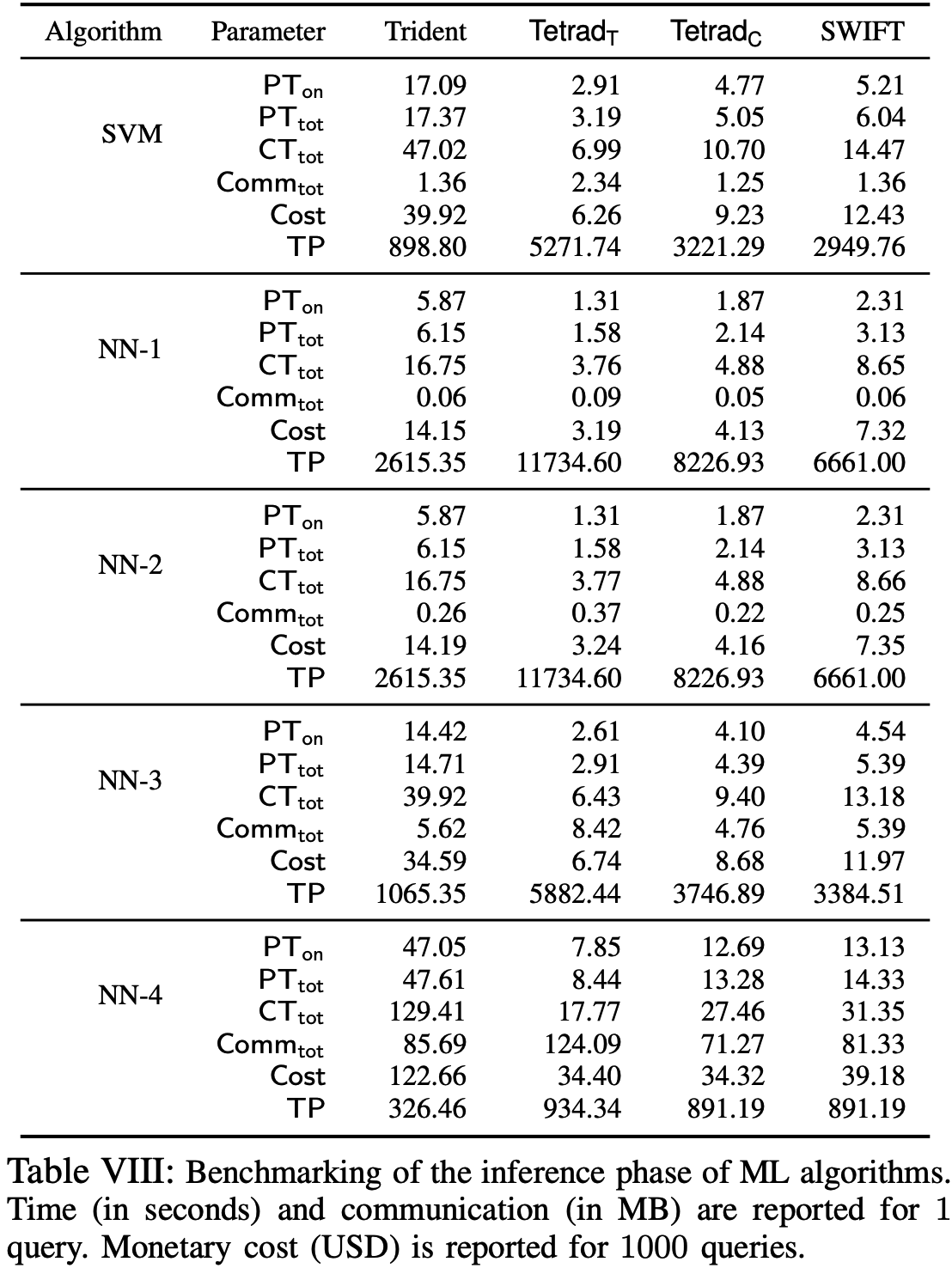
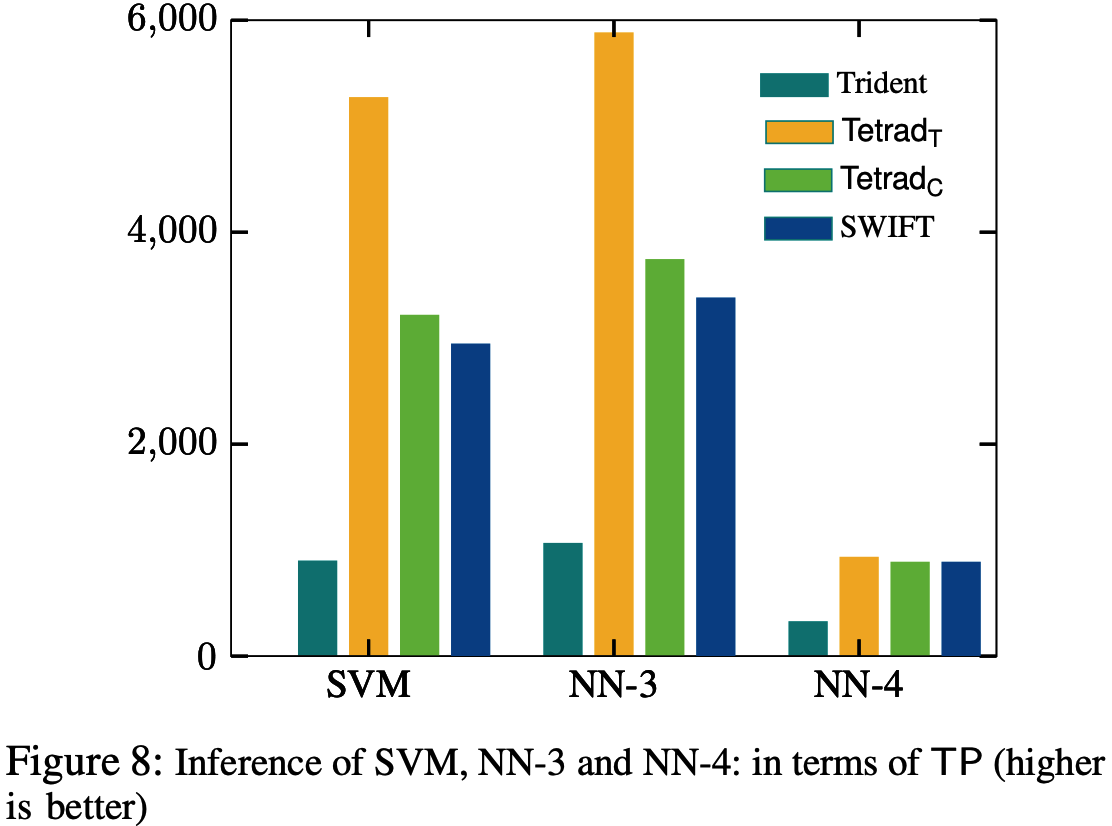
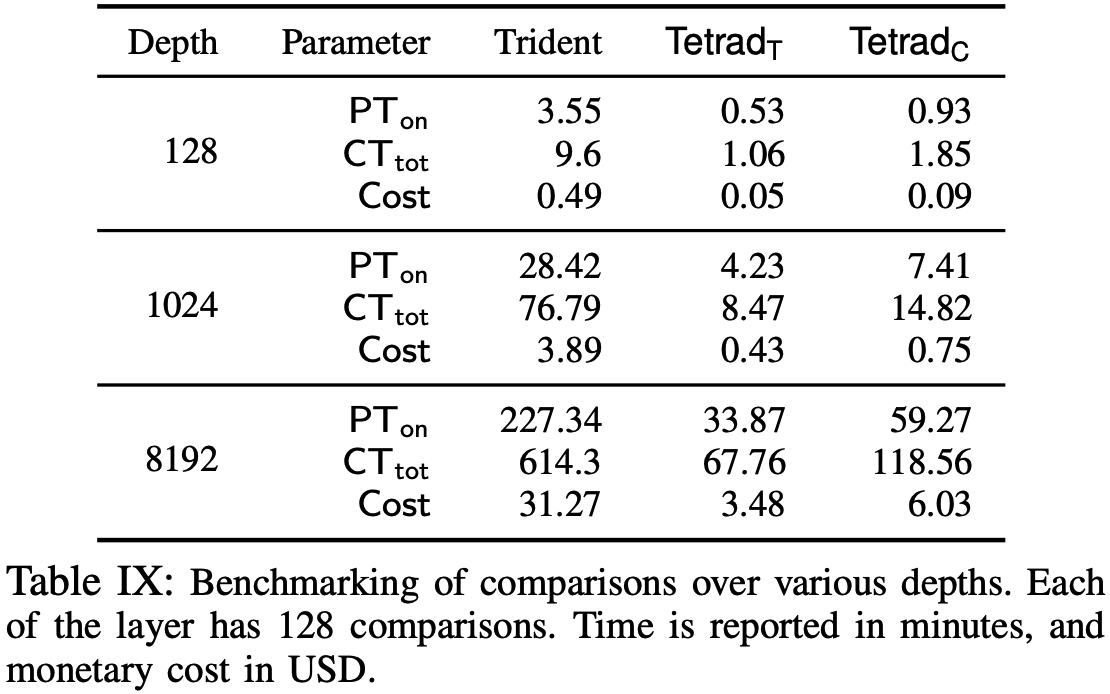
Conclusions

Tetrad是一个遵循离线-在线范式的主动安全的4PC机器学习框架, 分别实现了Fairness和GOD, 所使用的底层秘密共享语义和Trident框架基本相同, 主要的不同点在于四方份额分布以及在不同阶段中所起的作用, 协议设计在原理上并没有太大差别, 所构造协议的通信效率有所改进. Trident实现Fairness的核心思想则与Trident相同, 由于四方中只有一个腐化方, 因此验证阶段可以使其他诚实方达成一致的继续/中止信号. Tetrad实现GOD的核心思想结合了FALSH、SWIFT的思想, 通过Robust Joint-Send原语发现恶意行为后选出某个诚实方作为TTP进行明文计算, 此时不考虑对诚实方保持隐私, 因此Tetrad并不满足FaF安全性(Friends-and-Foes Security, CRYPTO'20).

References

[1] M. Byali, H. Chaudhari, A. Patra, and A. Suresh, “FLASH: Fast and robust framework for privacy-preserving machine learning,” PoPETs, vol. 2020, no. 2, pp. 459–480, Apr. 2020.

[2] H. Chaudhari, R. Rachuri, and A. Suresh, “Trident: Efficient 4PC framework for privacy preserving machine learning,” in NDSS 2020. The Internet Society, Feb. 2020.

[3] P. Mohassel and P. Rindal, “ABY3: A mixed protocol framework for machine learning,” in ACM CCS 2018, D. Lie, M. Mannan, M. Backes, and X. Wang, Eds. ACM Press, Oct. 2018, pp. 35–52.

[4] S. Wagh, D. Gupta, and N. Chandran, “SecureNN: 3-party secure computation for neural network training,” PoPETs, vol. 2019, no. 3, pp. 26–49, Jul. 2019.

[5] N. Koti, M. Pancholi, A. Patra, and A. Suresh, “SWIFT: Super-fast and Robust Privacy-Preserving Machine Learning,” in USENIX Security’21, 2021.

[6] I.Damga ̊rd,D.Escudero,T.K.Frederiksen,M.Keller,P.Scholl,and N. Volgushev, “New primitives for actively-secure MPC over rings with applications to private machine learning,” in 2019 IEEE Symposium on Security and Privacy. IEEE Computer Society Press, May 2019, pp. 1102–1120.

[7] A. Patra, T. Schneider, A. Suresh, and H. Yalame, “ABY2.0: Improved Mixed-Protocol Secure Two-Party Computation,” in USENIX Security’21, 2021.

[8] A. Dalskov, D. Escudero, and M. Keller, “Fantastic Four: Honest-Majority Four-Party Secure Computation With Malicious Security,” in USENIX Security’21, 2021.

本文标题: Tetrad: Actively Secure 4PC for Secure Training and Inference
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16553844634309.html
本站文章采用知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间: 2022-06-16T21:01:03+08:00

	\(P_0\)	\(P_1\)	\(P_2\)	\(P_3\)
\([\cdot]\)-sharing	—	\(v^1\)	\(v^2\)	—
\((\!(\cdot)\!)\)-sharing	—	\(v^1\)	\(v^2\)	\(v^3\)
\(\langle\cdot\rangle\)-sharing	—	\((v^1,v^3)\)	\((v^2,v^3)\)	\((v^1,v^2)\)
\([\![\cdot]\!]\)-sharing	\((\lambda_v^1,\lambda_v^2,\lambda_v^3)\)	\((m_v,\lambda_v^1,\lambda_v^3)\)	\((m_v,\lambda_v^2,\lambda_v^3)\)	\((m_v,\lambda_v^1,\lambda_v^2)\)