云中雨雾

    Trident: Efficient 4PC Framework for Privacy Preserving Machine Learning

    2022/05/13 10:33 上午 标签: #隐私保护机器学习

    今天给大家带来的是发表于NDSS'20上的文章Trident: Efficient 4PC Framework for Privacy Preserving Machine Learning, 原文链接: https://arxiv.org/pdf/1912.02631.pdf

    Abstract

    本文提出环上遵循离线-在线范式的具有主动安全的四方隐私保护机器学习框架Trident, 可抵抗一个恶意敌手, 同时还实现了公平性(Fairness). 与三方的ABY3相比, 本文通过在离线阶段引入一个额外诚实方, 并尽可能少地使用昂贵的电路来提升效率, 例如截断技术不影响乘法的在线开销, 离线阶段不需要任何电路, 而在线阶段则只涉及三方计算; B2A转化在通信轮次上有7倍改进, 通信复杂度有18倍改进. 本文所提出的混合计算协议支持秘密份额在Arithmetic、Boolean、Garbled World上进行高效转换, 而且具有恒定的轮复杂度, 适合安全外包计算场景. 最后本文与ABY3在64比特环上就LAN和WAN设定进行了实验对比, 发现训练阶段快187倍, 推理阶段快158倍.

    Introduction

    目前的MLaaS对于不同的终端用户有两种工作模式: 一是公司提供训练好的模型, 用户通过查询得到预测结果; 二是多个客户/公司使用他们的数据联合训练共同模型, 但不希望明文分享他们的数据. 但两种模式都需要用户做出一定的妥协, 对于前者用户会泄漏了查询结果, 对于后者公司在未经客户同意的情况下相互共享数据可能违反数据安全保护的相关法律法规, 此外由于竞争的缘故, 公司也不愿意泄漏自己的数据. 由此展现了隐私保护机器学习(PPML)的重要性.

    MPC虽然已经被证明是实用的, 但在诚实大多数假设下且参与方数量较少时MPC更为流行. 目前最好的三方PPML框架在半诚实安全下是高效的, 但在恶意安全下效率很低, 其主要原因是底层算子(如点积、比较、截断等)在恶意安全模型下通信开销更高, 例如ABY3的点积协议的通信量与向量长度线性相关, 由于这些算子需要多次执行, 尤其是在训练阶段, 因此为这些算子构造更高效的协议对构造高效PPML框架是至关重要的.

    尽管MPC效率得到了提升, 但最好的MPC协议并不能直接应用于PPML, 主要原因如下:

    1. 不同的MPC技术在算术、布尔、Yao世界中的效率各不相同, 单一世界可能更适合某些类型的计算, 因而在混合世界中执行协议比在单一世界中执行更高效.
    2. 非线性算子的计算问题. 当进行多次定点乘法后, 定点数精度会造成溢出, 为此需要进行定点截断, 在2PC下可以使用SecureML中的本地截断, 但在3PC/4PC下存在ABY3中所描述的攻击, 此外ABY3的方法依赖于开销较大的Ripple Carry Adder来构造协议, 因此需要探索更有效的定点截断技术. 此外, 激活函数的计算问题也是影响MPC效率的一大原因.

    总的来说, 本文的主要贡献如下:

    1. 高效4PC协议: 提出了一个环上具有主动安全的高效四方计算协议, 遵循离线-在线范式, 在线阶段每次乘法计算仅通信3个环元素且不需要第四方参与计算. 此外, 还在不影响乘法门复杂度的前提下实现了公平性.
    2. 快速混合世界计算: 本文提出的Trident框架可在算术、布尔、Garbled World之间相互转换, 协议构造侧重于在线阶段的高吞吐量, 主要通过额外的诚实的第四方来达到, 与ABY3相比更高效.
    3. 高效截断: 本文提出的截断协议可与本文的乘法协议结合使用, 在线阶段无需额外开销, 且不需要像ABY3一样借助RCA来构造, 效率更高.
    4. 安全比较: 本文提出的安全比较协议具有常数轮复杂度.
    5. 机器学习模块: 本文提出的激活函数安全计算协议具有常数轮复杂度.
    6. 实验: 在LAN和WAN下与ABY3在线性回归、逻辑回归、神经网络、卷积神经网络的训练和预测等几个方面进行了性能测试, 结果如下:
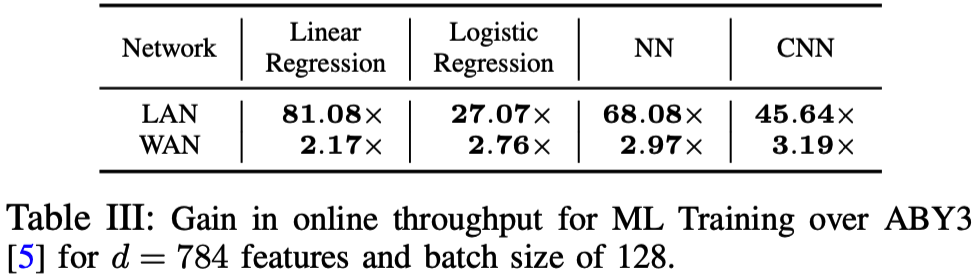
    image-20220511172947213

    Preliminaries and Definitions

    符号约定: 四方集合\(\mathcal P=\{P_0,P_1,P_2,P_3\}\), 同步网络, 通过点对点安全信道连接. 抗碰撞哈希函数\(\mathsf H\).

    为减少通信开销生成共同随机性, 参与方通过预共享密钥设置建立PRF使用的预共享随机密钥来生成相关随机性.

    4PC Protocol

    Sharing Semantics

    设秘密为\(v\), 计算域为布尔环\(\mathbb Z_2\)和算术环\(\mathbb Z_{2^\ell}\). 本文涉及三种不同的Sharing:

    • \([\cdot]\)-sharing: \(P_1,P_2,P_3\)三方下的加法秘密共享(ASS), \(P_i\)的份额为\([v]_{P_i}=v_i\), 满足\(v=v_1+v_2+v_3\).
    • \(\langle\cdot\rangle\)-sharing: \(P_1,P_2,P_3\)三方下的复制秘密共享(RSS), \(P_1\)的份额为\(\langle v\rangle_{P_1}=(v_2,v_3)\), \(P_2\)的份额为\(\langle v\rangle_{P_2}=(v_3,v_1)\), \(P_3\)的份额为\(\langle v\rangle_{P_3}=(v_1,v_2)\), 满足\(v=v_1+v_2+v_3\).
    • \([\![\cdot]\!]\)-sharing: \(P_0,P_1,P_2,P_3\)四方下的秘密共享, 存在\(\lambda_v,m_v\in\mathbb Z_{2^\ell}\), 使得\(m_v=v+\lambda_v\), 其中\(\lambda_v\)通过\(\langle\cdot\rangle\)-sharing共享, \(P_1,P_2,P_3\)则有明文形式的\(m_v\). 最终\(P_0\)的份额为\([\![v]\!]_{P_0}=(\lambda_{v,1},\lambda_{v,2},\lambda_{v,3})\), \(P_1\)的份额为\([\![v]\!]_{P_1}=(m_v,\lambda_{v,2},\lambda_{v,3})\), \(P_2\)的份额为\([\![v]\!]_{P_2}=(m_v,\lambda_{v,3},\lambda_{v,1})\), \(P_3\)的份额为\([\![v]\!]_{P_3}=(m_v,\lambda_{v,1},\lambda_{v,2})\). 记\([\![v]\!]=(m_v,\langle \lambda_v\rangle)\)为\(v\)的\([\![\cdot]\!]\)份额.

    不同秘密共享下各参与方份额总结如下:

    类型 \(P_0\) \(P_1\) \(P_2\) \(P_3\)
    \([\cdot]\)-sharing — \(v_1\) \(v_2\) \(v_3\)
    \(\langle\cdot\rangle\)-sharing — \((v_2,v_3)\) \((v_3,v_1)\) \((v_1,v_2)\)
    \([\![\cdot]\!]\)-sharing \((\lambda_{v,1},\lambda_{v,2},\lambda_{{v,3}})\) \((m_v,\lambda_{v,2},\lambda_{v,3})\) \((m_v,\lambda_{v,3},\lambda_{v,1})\) \((m_v,\lambda_{v,1},\lambda_{v,2})\)

    以上秘密共享方案都满足线性性, 因此计算线性算子不需要交互.

    Building Blocks

    • 秘密分发协议\(\Pi_\mathsf{Sh}(P_i,v)\): 允许\(P_i\)分发他拥有的秘密\(v\), 使得参与方得到\([\![v]\!]\). 离线阶段不需要通信, 在线阶段需要1轮, \(3\ell\)比特均摊通信量. 具体协议过程如下:
    image-20220331170244609
    • 秘密分发协议\(\Pi_\mathsf{aSh}(P_0,v)\): 特别地, \(P_0\)可在离线阶段分发他的秘密\(v\), 生成\(\langle v\rangle\). 需要1轮通信, \(2\ell\)比特均摊通信量. 具体协议过程如下:
    image-20220331170943882
    • 秘密重构协议\(\Pi_\mathsf{Rec}(\mathcal P,[\![v]\!])\): 给定\([\![v]\!]\), \(\mathcal P\)中的参与方重构\(v\). 每个参与方从另一方接收所缺失的份额并从第三方接收该缺失份额的哈希值以验证一致性. 在线阶段需要1轮, \(4\ell\)比特均摊通信量. 具体协议过程如下:
    image-20220331171802084

    States of 4PC Protocol

    4PC协议可分为输入共享(Input Sharing)、求值(Evaluation)、输出重构(Output Reconstruction)三个阶段. 输入共享阶段主要是通过秘密分发协议\(\Pi_\mathsf{Sh}\)来执行, 输出重构阶段主要是通过秘密重构协议\(\Pi_\mathsf{Rec}\)来执行, 下面主要介绍求值阶段, 因为加法门可以本地计算, 因此这里仅介绍计算乘法门的协议\(\Pi_\mathsf{Mult}\), 即给定\([\![x]\!], [\![y]\!]\), 安全计算\([\![z]\!]\), 其中\(z=xy\).

    离线阶段的主要任务是让\(P_1,P_2,P_3\)生成\(\gamma_{xy}=\lambda_x\lambda_y\)的RSS份额\(\langle \gamma_{xy}\rangle\). 首先\(P_1,P_2,P_3\)本地计算\([\gamma_{xy}]\), 然后通过resharing交换份额得到\(\langle \gamma_{xy}\rangle\). 在交换\(\gamma_{xy}\)的份额之前, 为防止泄漏, 参与方需要在份额上加入Zero sharing的份额. 此外, \(P_0\)辅助其他参与方验证收到的份额的正确性. 在线阶段的目标是计算\(m_z\), 因为

    \[\begin{aligned} m_z&=z+\lambda_z=xy+\lambda_z=(m_x-\lambda_x)(m_y-\lambda_y)+\lambda_z\\ &=m_xm_y-\lambda_xm_y-\lambda_ym_x+\lambda_x\lambda_y+\lambda_z, \end{aligned} \]

    \(P_1,P_2,P_3\)可以本地计算\(m_z'=m_z-m_xm_y\)的\([\cdot]\)份额, 然后交换份额重构\(m_z'\). 由于\([\cdot]\)-sharing的特性, 每个缺失的份额都可被两方计算, 因此各参与方通过让一方发送缺失的份额, 另一方发送与之对应的哈希值, 以可验证的方式重构出\(m_z\). 一个关键的优化点是, 每个乘法门交换哈希值可以推迟到输出重构阶段合并进行, 所有相对应的值并在一起再计算哈希值, 从而可将整体通信量减少为3个环元素. 完整的乘法计算协议如下, 离线阶段需要1轮, \(3\ell\)比特均摊通信量, 在线阶段需要1轮, \(3\ell\)比特均摊通信量.

    image-20220331200635965

    Achieving Fairness

    公平性要求所有参与方要么都得到输出, 要么都中止协议. 因此实现公平性需要确保所有参与方在输出重构阶段都是alive的, 同时还需要阻止敌手发起选择中止攻击(selective abort attack), 即敌手让某些诚实参与方中止协议. 若乘法门验证通过, \(P_1,P_2,P_3\)设定比特\(b=\mathtt{continue}\), 否则设定\(b=\mathtt{abort}\), 然后发送\(b\)给\(P_0\). 若\(P_0\)发现某个参与方发送了abort, 则向所有参与方发送abort, 从而确保所有参与方aliveness. 剩余的参与方然后交换他们来自\(P_0\)的回复(continue/abort), 根据其中的多数来决定继续还是中止. 因为仅有一个恶意方, 因此所有参与方将在同一状态下, 从而防止敌手发起选择中止攻击. 若参与方决定继续, 则他们交换缺失的份额. 基于至多只有一个恶意方的事实和秘密共享方案的构造, 收到次数最多的缺失份额将在诚实参与方中保持一致性. 完整的公平重构协议如下, 在线阶段需要4轮, \(8\ell\)比特均摊通信量.

    Trident5

    Mixed Protocol Framework

    混合协议框架主要考虑三个世界: Arithmetic world (A)、Boolean world (B)、Garbled world (G).

    The Garbled World

    对于混淆世界, 将3PC的MRZ协议(CCS'15)扩展到4PC. 在4PC下, \(P_1,P_2,P_3\)作为混淆方, \(P_0\)作为求值方. 作为优化, \(P_0\)可以只分享他的输入给\(P_1,P_2\), 而不是所有方. 对于交叉检验, \(P_1\)发送混淆电路给\(P_0\), 同时\(P_2\)发送与之相对应的哈希值给\(P_0\). 同时方案整合了Free-XOR、half-gate、fixed-key AES garbling技术. 本文提供了单比特的协议, 可以通过并行\(\ell\)次来支持\(\ell\)比特的值.

    • 秘密共享语义: 对于比特\(v\), \([\![v]\!]^\mathbf G\)被定义为\([\![v]\!]_{P_i}^\mathbf G=K_v^0\in\{0,1\}^\kappa\), \(i\in\{1,2,3\}\), 和\([\![v]\!]_{P_0}^\mathbf G=K_v^v=K_v^0\oplus vR\), 其中\(\kappa\)是计算安全参数, \(R\)是由\(P_1,P_2,P_3\)通过预分享随机性生成的最后一比特(最低位)为1的全局偏移量, 且\(R\)是所有\([\![\cdot]\!]^\mathbf G\)-sharing中共有的. 容易证明, \(\mathsf{LSB}([\![v]\!]_{P_i}^\mathbf G)\oplus\mathsf{LSB}([\![v]\!]_{P_0}^\mathbf G)=v\). 简单起见, 当\(v\in\mathbb Z_{2^\ell}\)时, 用\([\![v]\!]^\mathbf G\)表示\(v\)的每个比特的\([\![\cdot]\!]^\mathbf G\)份额的集合.

    • 输入共享: 输入共享协议\(\Pi_\mathsf{Sh}^\mathbf{G}(P_i,v)\)使得\(P_i\)生成\([\![v]\!]^\mathbf{G}\). 在协议中, \(P_0\)需要确保得到正确的\(K_v^v\). 为此, 需要让混淆方向\(P_0\)承诺混淆电路的密钥, 然后\(P_0\)通过交叉验证所收到的承诺来验证正确性. 具体过程如下:

    image-20220401113704731

    若\(P_i=P_0\), 则\(P_0\)采样随机比特\(v_1\), 计算\(v_2=v\oplus v_1\), 分别发送\(v_1,v_2\)给\(P_1,P_2\). 然后参与方分别执行\(\Pi_\mathsf{Sh}^\mathbf G(P_1,v_1)\)和\(\Pi_\mathsf{Sh}^\mathbf G(P_2,v_2)\), 分别得到\([\![v_1]\!]^\mathbf G\)和\([\![v_2]\!]^\mathbf G\). 然后参与方通过free-XOR技术本地计算\([\![v]\!]^\mathbf G=[\![v_1]\!]^\mathbf G\oplus[\![v_2]\!]^\mathbf G\). 此时承诺的密钥不需要置换, 因为\(P_0\)已知\(v_1\)和\(v_2\). 作为优化, \([\![v_1]\!]^\mathbf G\)的计算可以转移到离线阶段.

    • 输出重构: 若\(P_i=P_0\), 则\(P_1,P_2\)发送他们份额的最后一比特给\(P_i\), 然后\(P_i\)验证所收到的值是否相同. 若\(P_i\)是其中一个混淆方, 则\(P_0\)发送它的份额为\(P_i\). 由于底层混淆电路的可靠性(authenticity), 腐化的\(P_0\)不能发送错误的份额给\(P_i\). 若面向\(P_i\in\{P_1,P_2,P_3\}\)有多个重构, 则\(P_0\)可以发送它份额的最后一比特连同所有相应份额的哈希值.

    • 基本算子: 设\(u,v\in\{0,1\}\)通过\([\![\cdot]\!]^\mathbf G\)-sharing秘密共享, \(P_1,P_2,P_3\)持有份额\((K_u^0\oplus uR,K_v^0\oplus vR)\). 令\(c\)表示输出.

      • XOR: 参与方本地计算\([\![c]\!]^\mathbf G=[\![u]\!]^\mathbf G\oplus[\![v]\!]^\mathbf G\);
      • AND: 离线阶段, \(P_1,P_2,P_3\)采样随机\(K_c^0\in\{0,1\}^\kappa\), 计算\(K_c^1=K_c^0\oplus R\), 然后构造AND门的混淆表. \(P_1\)发送混淆表给\(P_0\), 同时\(P_2\)发送表的哈希值给\(P_0\). 在线阶段, \(P_0\)对电路进行求值, 得到\([\![c]\!]_{P_0}^\mathbf G=K_c^c\). 对\(i\in\{1,2,3\}\), \(P_i\)设定\([\![c]\!]_{P_i}^\mathbf G=K_c^0\).

    Building Blocks

    • 可验证的算术/布尔份额: 协议\(\Pi_\mathsf{vSh}\)允许\(P_i,P_j\)以可验证的方式生成\([\![v]\!]\). 简单来说, \(P_i\)执行\(\Pi_\mathsf{Sh}(P_i,v)\), 同时\(P_j\)发送\(\mathsf{H}(m_v)\)给\(P_1,P_2,P_3\)辅助验证. 具体过程如下图7, 离线阶段不需要交互, 在线阶段需1轮, 至多\(2\ell\)比特均摊通信量. 若\(P_1,P_2,P_3\)都已知\(v\), 则可令\(\lambda_{v,1}=\lambda_{v,2}=\lambda_{v,3}=0\)和\(m_v=v\), 从而让参与方不需要交互即可生成\([\![v]\!]\).
    image-20220401154559068
    • 可验证的Garbled Sharing: 协议\(\Pi_\mathsf{vSh}^\mathbf G(P_i,P_j,v)\)允许\(P_i,P_j\)以可验证的方式生成\([\![v]\!]^\mathbf G\). 当\(P_i,P_j\)都是混淆方时, 其中一方可以发送密钥, 同时另一方发送相对应的哈希值以检测一致性. 若\(P_j=P_0\), 则\(P_1,P_2\)依序发送密钥的承诺给\(P_0\). 此外, \(P_i\)发送实际密钥的解承诺给\(P_0\). 具体协议过程如下图, 离线阶段不需要交互, 在线阶段需要1轮, 均摊通信量为\(\kappa\)比特.
    image-20220401163115929
    • 点积计算协议\(\Pi_\mathsf{DotP}(\vec{\mathbf x},\vec{\mathbf y})\rightarrow z\): 给定长度为\(d\)的向量\(\vec{\mathbf x},\vec{\mathbf y}\), 计算\(z=\vec{\mathbf x}\odot\vec{\mathbf y}\). 协议的构造思路与乘法协议类似, 为了让通信开销独立于向量长度, 对于\(j\in\{1,\cdots,d\}\), 在线阶段不逐个重构\(x_j\cdot y_j\), 参与方本地将所有乘积结果累加在一起然后只通信一次, 从而减少\(d\)倍的通信开销. 具体协议过程如下, 离线阶段需要1轮, 均摊通信量为\(3\ell\)比特, 在线阶段需要1轮, 均摊通信量为\(3\ell\)比特.
    TRIDENT9

    Sharing Conversions

    • Garbled to Boolean Sharing (G2B): 离线阶段, \(P_1,P_2\)首先使用预共享随机性生成随机值\(r\), 然后分别生成\([\![r]\!]^\mathbf G,[\![r]\!]^\mathbf B\). 此外, 他们还通信计算两比特XOR的混淆电路及其解码信息给\(P_0\). 在线阶段, \(P_0\)进行求值得到\(v\oplus r\), 并发送结果及其相应密钥的哈希值给\(P_3\). 混淆电路的可靠性保证了腐化的\(P_0\)不能发送错误的比特, 因为它无法猜中与之对应的密钥. 具体转换过程如下:
    image-20220401173812263
    • Garbled to Arithmetic Sharing (G2A): 与G2B类似, 主要的不同之处在于将混淆电路的XOR变为两个\(\ell\)比特数的加减法电路计算. 具体转换过程如下:
    image-20220401200952578
    • Boolean to Garbled Sharing (B2G): 由于在布尔世界中, 比特\(v=(m_v\oplus\lambda_{v,1})\oplus(\lambda_{v,2}\oplus\lambda_{v,3})\), 若参与方可得到\(x=(m_v\oplus\lambda_{v,1})\)和\(y=(\lambda_{v,2}\oplus\lambda_{v,3})\), 则可以通过free-XOR技术本地计算\(v\). 具体转换过程如下:
    image-20220401203633114
    • Arithmetic to Garbled Sharing (A2G): 类似于B2G, \(v=(m_v-\lambda_{v,1})-(\lambda_{v,2}+\lambda_{v,3})\), 参与方调用\(\Pi_\mathsf{vSh}^\mathbf G\)可验证地生成\(x=(m_v-\lambda_{v,1})\)和\(y=(\lambda_{v,2}+\lambda_{v,3})\)的混淆份额\([\![x]\!]^\mathbf G,[\![y]\!]^\mathbf G\). 在线阶段, 参与方对混淆减法电路进行求值得到\(v=x-y\)的份额. 具体转换过程如下:
    TRIDENT13
    • Arithmetic to Boolean Sharing (A2B): 类似于A2G, 主要的不同之处是参与方生成\(x=(m_v-\lambda_{v,1})\)和\(y=(\lambda_{v,2}+\lambda_{v,3})\)的布尔份额\([\![x]\!]^\mathbf B,[\![y]\!]^\mathbf B\), 并对比布尔减法电路进行求值计算\(v=x-y\)的布尔份额\([\![v]\!]^\mathbf B\). 具体转换过程如下:
    image-20220401214226880
    • Bit to Arithmetic Sharing (Bit2A): 计算\([\![b]\!]^\mathbf B\rightarrow[\![b]\!]\). 设\(u,v\)分别表示在环\(\mathbb Z_{2^\ell}\)上的比特\(\lambda_{b},m_b\). 根据\(b=m_b\oplus\lambda_b=v+u-2vu\), \(P_0\)在离线阶段生成\(\langle u \rangle\). 为了确保份额的正确性, \(P_1,P_2,P_3\)检验是否满足等式\((\lambda_b\oplus r_b)'=u+r_b'-2ur_b'\), 其中\(a'\)表示比特\(a\)在环\(\mathbb Z_{2^\ell}\)上的对应值. 通过验证后, 参与方本地转换\(\langle u\rangle\)为\([\![u]\!]\). 在在线阶段, 参与方计算\(u\)和\(v\)的秘密份额乘积\([\![uv]\!]\), 然后本地计算\([\![b]\!]=[\![v]\!]+[\![u]\!]-2[\![uv]\!]\). 需要注意的是当执行\(\Pi_\mathsf{Sh}(P_1,P_2,P_3,v)\)时, \(\lambda_v=0\), 所以计算乘法时不需要\(\gamma_{uv}\)的份额. 具体转换过程如下:
    TRIDENT15

    • Boolean to Arithmetic Sharing (B2A): 利用事实\(v=\sum_{i=0}^{\ell-1}2^i\cdot v_i\), 其中\(v_i\)代表环\(\mathbb Z_{2^\ell}\)上的值\(v\)的第\(i\)比特. 可利用关系\(v=\sum_{i=0}^{\ell-1}2^i\cdot v_i=\sum_{i=0}^{\ell-1}2^i\cdot(m_{v_i}\oplus\lambda_{u_i})=\sum_{i=0}^{\ell-1}2^i\cdot (m_{v_i}'+\lambda_{u_i}'-2m'_{v_i}\cdot\lambda_{u_i}')\), 其中\(m_{v_i}',\lambda_{u_i}'\)分别表示环\(\mathbb Z_{2^\ell}\)上的比特\(m_{v_i}\)和\(\lambda_{u_i}\).

      B2A的离线阶段与Bit2A类似, 具体转换过程如下:

    image-20220403092405398

    • Bit Injection (BitInj): 计算\([\![b]\!]^\mathbf B[\![v]\!]\rightarrow[\![bv]\!]\). 在环\(\mathbb Z_{2^\ell}\)上, 令\(y_1=\lambda_b\), \(y_2=\lambda_b\lambda_v\). 类似地, 令\(x_0=m_bm_v\),\(x_1=m_b\),\(x_2=m_v-2m_vm_b\),\(x_3=2m_b-1\), 则\(b\cdot v=(m_b\oplus\lambda_b)(m_v-\lambda_v)=x_0-x_1y_1+x_2y_2+x_3y_3\).

      在离线阶段, \(P_0\)生成\(\lambda_{b}'\)和\(\lambda_b\lambda_v\), 其中\(\lambda_{b}'\)表示环\(\mathbb Z_{2^\ell}\)上的比特. 检验\(\langle\lambda_b'\rangle\)的方法与\(\Pi_\mathsf{Bit2A}\)相同, 检验\(\langle\lambda_b\lambda _v\rangle\)的方法是计算\(\Pi_\mathsf{BitInj}\). 在线阶段, 参与方通过执行\(\Pi_\mathsf{vSh}\)本地计算\([b\cdot v]\), 最后参与方本地累加份额得到\([\![b\cdot v]\!]\). 具体转换过程如下:

    TRIDENT17

    不同转换协议的通信轮次和通信量与ABY3之间的对比如下, 其中\(\mathsf{G1}\)表示2输入减法混淆电路, \(\mathsf{G2}=\mathsf{Gar}(2,\mathsf{Sub},\ell)\)表示2输入减法混淆电路及其解码信息, 类似地定义\(\mathsf{G3}=\mathsf{Gar}(3,\mathsf{Sub},\ell)\), \(\mathsf{G4}=\mathsf{Gar}(3,\mathsf{Adder},\ell)\).

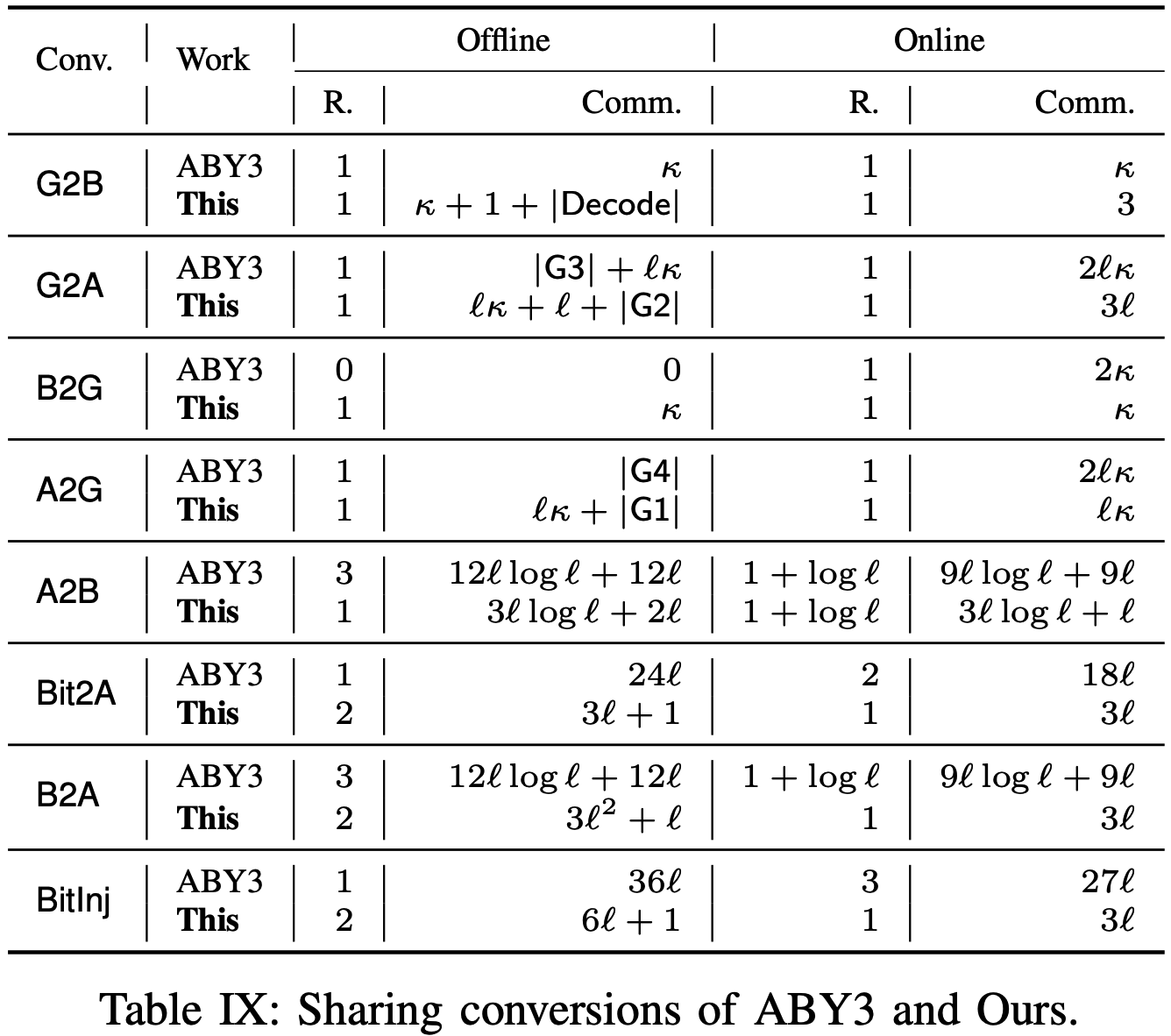
    image-20220403090623808

    Privacy Preserving Machine Learning

    使用\(\mathbb Z_{2^\ell}\)上的有符号补码(signed two's compliment)来表示运算中涉及的十进制数, 其中最高位(MSB)是符号位, 最后\(d\)位表示小数部分.

    Sharing Truncation

    与ABY3的概率截断方法类似: 首先生成随机截断对\((r,r^t)\), 其中\(r^t\)是\(r\)的截断值, 则\(z\)的截断值\(z^t\)可以通过首先恢复\(z-r\)再截断为\((z-r)^t\), 最后加上\(r^t\)得到, 即\(z^t=(z-r)^t+r^t\). 不同之处在于本文没有使用任何布尔电路, 从而将离线阶段轮复杂度改进为常数轮. 首先参与方非交互地生成\(\langle r\rangle\), 使得\(P_0\)得到\(r\). 然后\(P_0\)生成\([\![r^t]\!]\), \(P_1,P_2,P_3\)利用关系\(r=2^dr^t+r_d\)(带余除法)来验证\(P_0\)所生成的份额正确性, 其中\(r_d\)表示\(r\)的最后\(d\)比特. 具体份额截断协议如下:

    TRIDENT18

    正确性: 协议\(\Pi_\mathsf{MultTr}\)的离线阶段, 若腐化\(P_0\)生成了错误的\([\![r^t]\!]\)份额, 则\(P_1,P_2,P_3\)中止.

    证明: 只需证明\(m_1+m_2=c\), 其中\(m_1=r_2-2^dr_2^t-r_{d,2}+c\), \(m_2=(r_1+r_3)-2^d(r_1^t+r_3^t)-(r_{d,1}+r_{d,3})\). 注意到\(r=2^dr^t+r_d\), 所以有

    \[\begin{aligned} m_1+m_2&=(r_2-2^dr_2^t-r_{d,2}+c)+((r_1+r_3)-2^d(r_1^t+r_3^t)-(r_{d,1}+r_{d,3}))\\ &=(r_1+r_2+r_3)-2^d(r_1^t+r_2^t+r_3^t)-(r_{d,1}+r_{d,2}+r_{d+3})+c\\ &=(r)-(2^dr^t+r_d)+c=0+c=c. \end{aligned} \]

    Secure Comparison

    给定\(x,y\)的算术共享份额, 计算\(x<_?y\)的布尔共享份额. 在定点表示形式下, 最简单的方式是计算最高位\(\mathsf{MSB}(x-y)\). 为此可以通过构造比特抽取协议\(\Pi_\mathsf{BitExt}\)来完成. 本文中的比特抽取协议与ABY3类似. \(P_0,P_3\)离线阶段生成\(y=\lambda_{v,1}+\lambda_{v,2}\)的布尔份额, \(P_1,P_2\)在在线阶段生成\(x=m_v-\lambda_{v,3}\)的布尔份额. 然后参与方使用ABY3的优化的Parallel Prefix Adder (PPA)进行求值计算得到最高位的布尔份额.

    Activation Functions

    • ReLU: \(\mathsf{relu}(v)=\mathsf{max}(0,v)=(1\oplus b)v\), 其中比特\(b=1\Leftrightarrow v<0\). 因此参与方首先调用\(\Pi_\mathsf{BitExt}\)得到\([\![b]\!]^\mathbf B\), 本地计算\([\![1\oplus b]\!]^\mathbf B\). 最后调用\(\Pi_\mathsf{BitInj}\)计算\([\![1\oplus b]\!]^\mathbf B\cdot[\![v]\!]\).
    • Sigmoid: 使用SecureML中的分段近似函数来计算Sigmoid函数. 此时\(\mathsf{sig}(v)=(1\oplus{b}_1)b_2(v+1/2)+(1\oplus{b}_2)\), 其中\(v+1/2<0\Leftrightarrow b_1=1\), \(v-1/2<0\Leftrightarrow b_2=1\). 类似于计算ReLU的方法进行求解, 但需要额外调用一次\(\Pi_\mathsf{BitExt}\), \(\Pi^\mathbf B_\mathsf{Mult}\)和\(\Pi_\mathsf{BitInj}\).
    • Softmax: 使用SecureML中提出的变体来近似: \(\mathsf{smx}(u_i)=\frac{\mathsf{relu}(u_i)}{\sum_{j=1}^{n_f}\mathsf{relu}(u_j)}\). 除法则通过A2G和除法混淆电路来计算.

    Communication Cost

    以上机器学习相关的协议通信轮次和通信量与ABY3之间的对比如下:

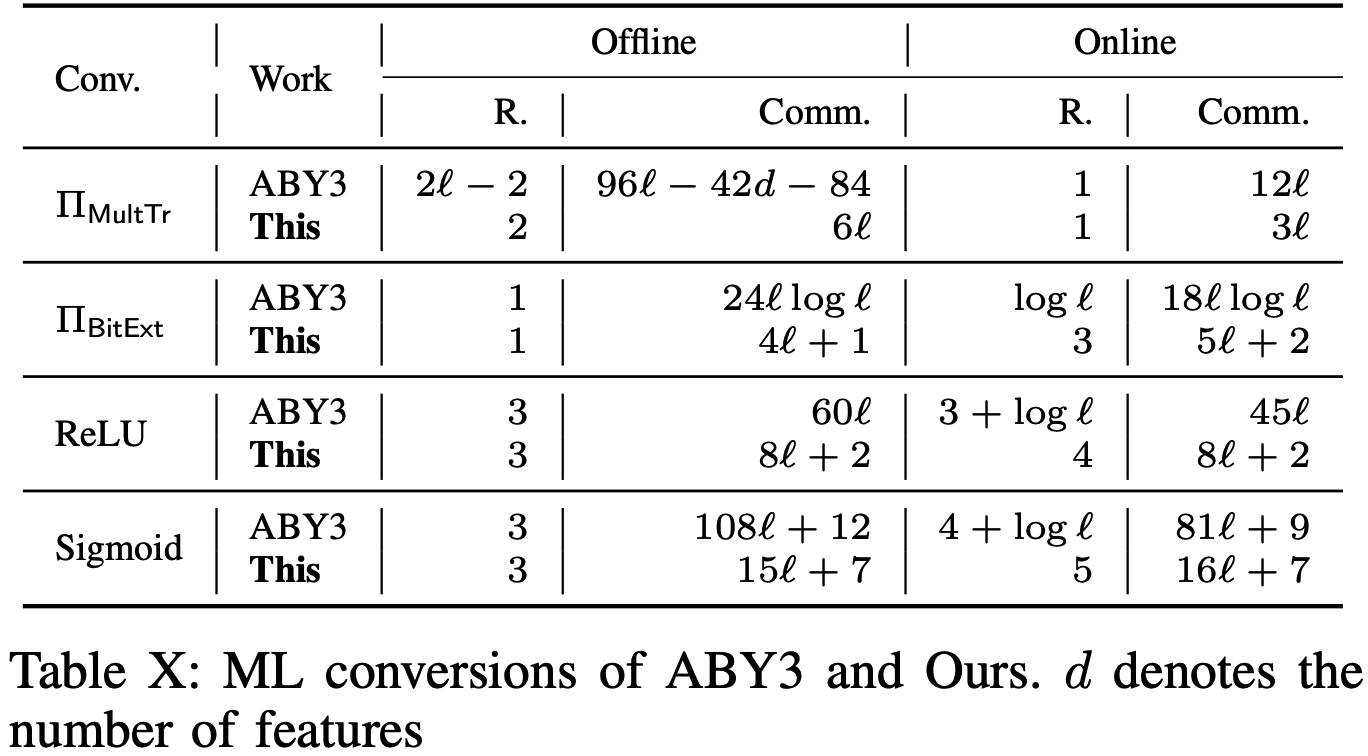
    image-20220403091656338

    Implementation and Benchmarking

    实验部分主要与ABY3的方案进行了比较, 实验内容为线性回归、逻辑回归、神经网络和卷积神经网络.

    Secure Training

    性能基准是LAN下计算每秒钟的迭代次数, WAN下计算每分钟的迭代次数.

    • 线性回归: LAN/WAN设定下与ABY3对比如下
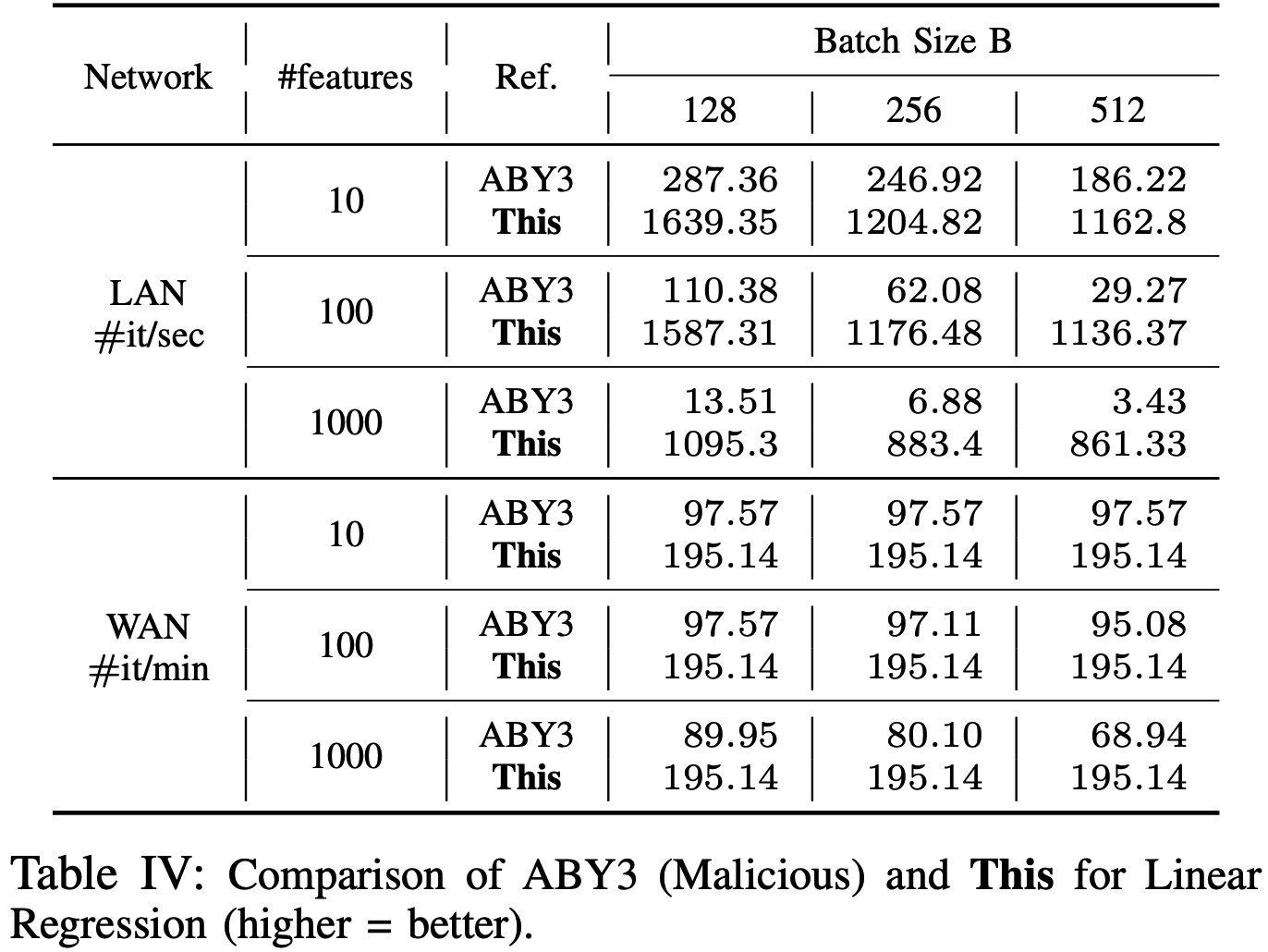
    image-20220403095347025
    • 逻辑回归: LAN/WAN设定下与ABY3的对比如下
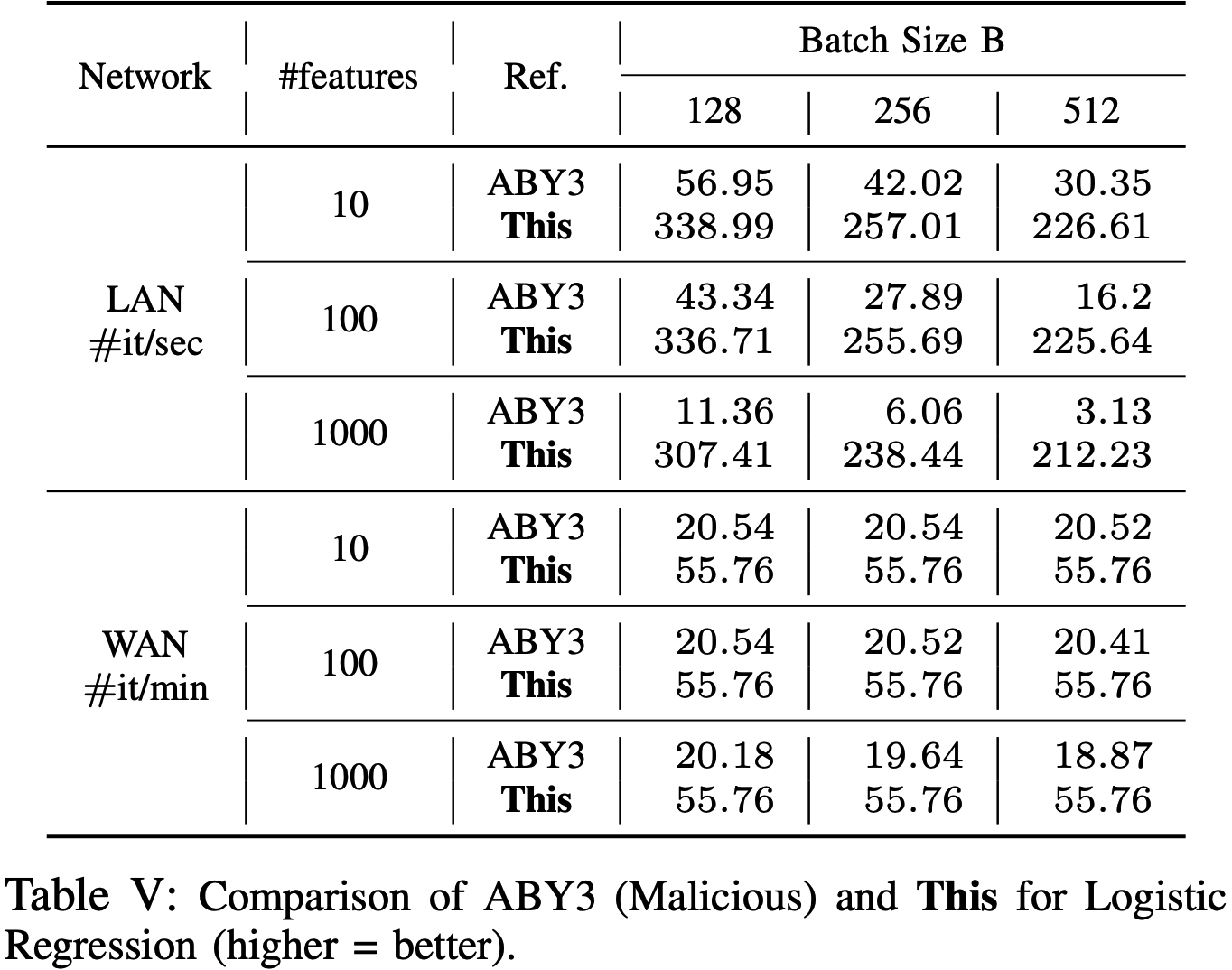
    image-20220403095722855
    • 神经网络: LAN/WAN设定下与ABY3的对比如下
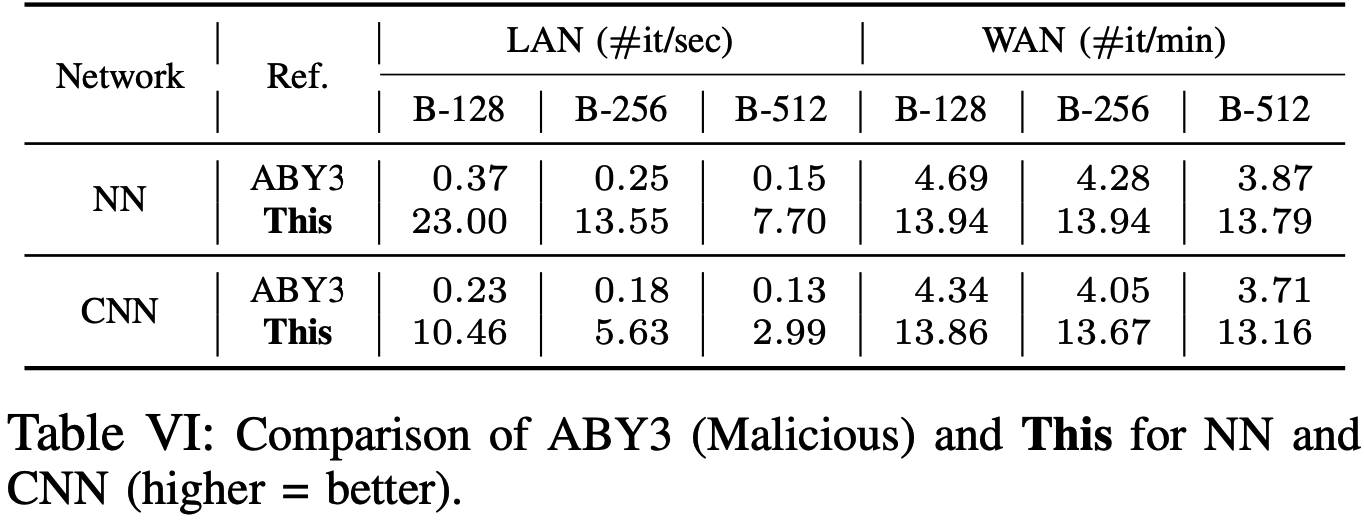
    image-20220403100021867

    Secure Prediction

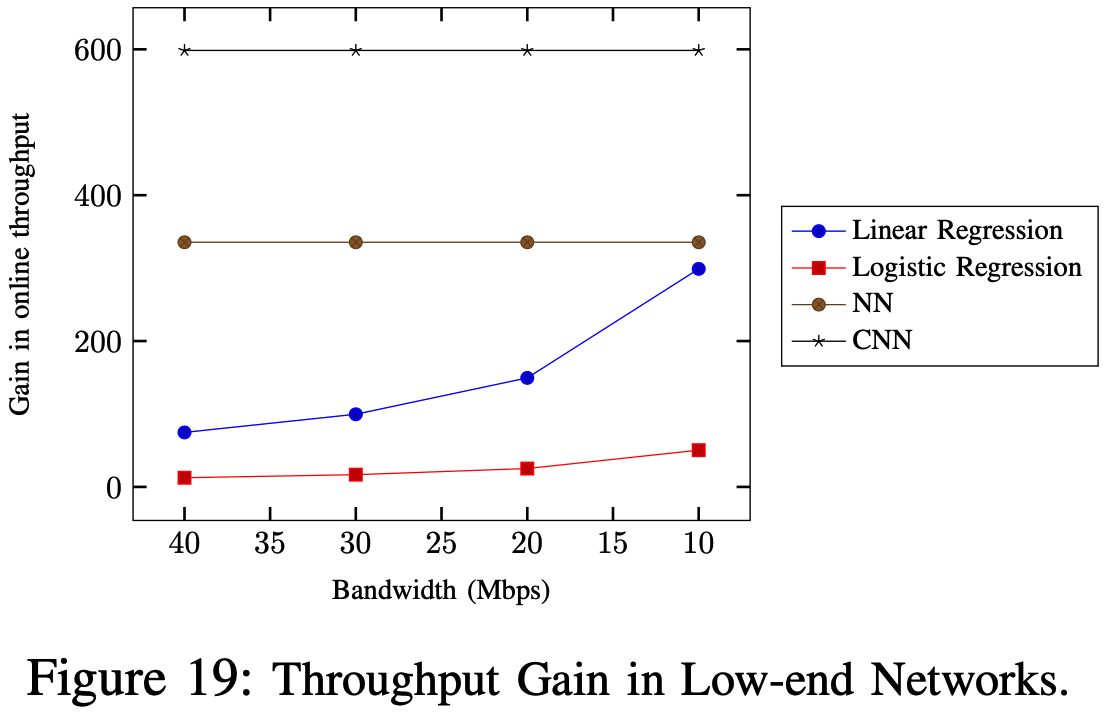
    以在线阶段的时延(Latency)作为基准, 结果如下:

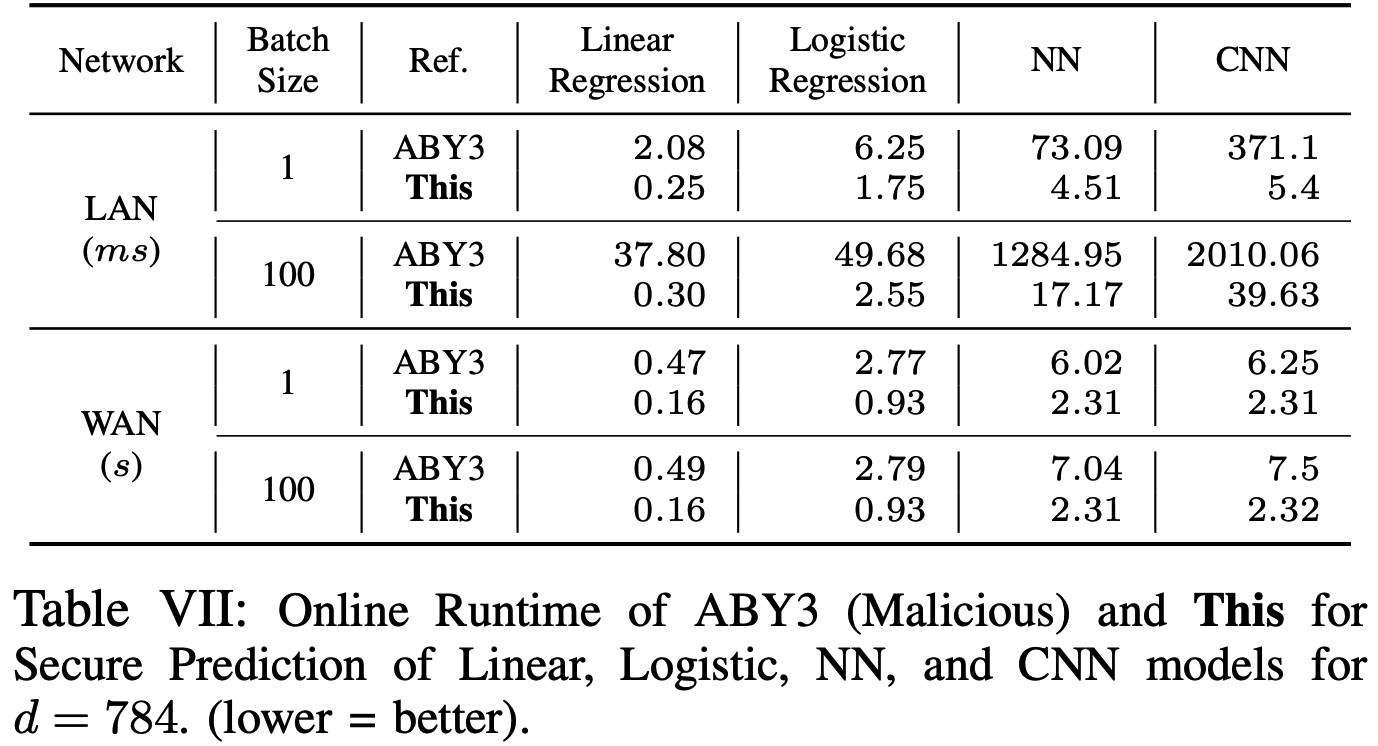
    image-20220403101045997

    LAN下在线吞吐量(每秒钟预测次数)和WAN下在线吞吐量(每分钟预测次数)与ABY3在不同数据集下的对比如下:

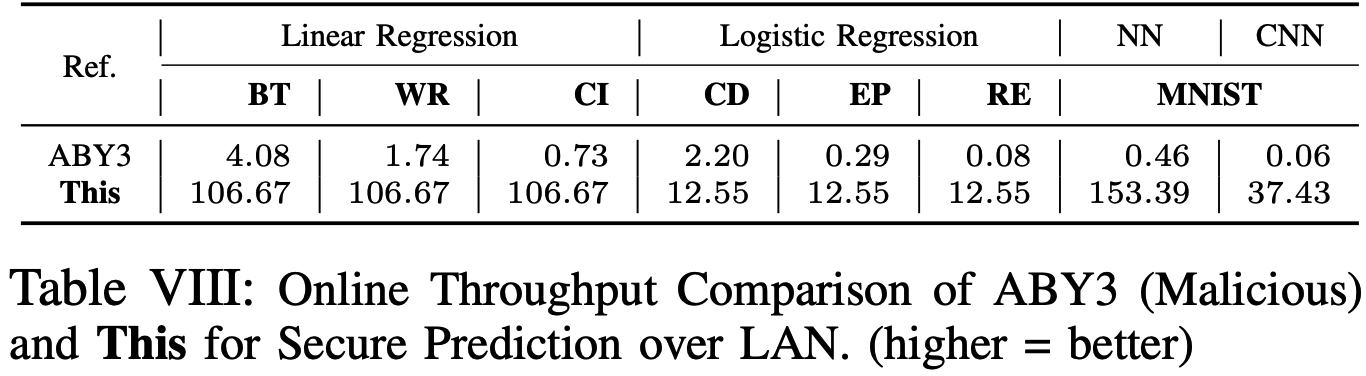
    image-20220403103318655 image-20220403103403019

    Conclusions

    Trident是一个遵循离线-在线范式的四方机器学习框架, 可抵抗1个恶意敌手. 与ABY3相比, Trident在离线阶段引入一个额外的计算方\(P_0\), 在构造协议时尽可能少地应用昂贵的电路, 在线阶段则主要是三方计算. 所提出的方案支持不同世界的份额之间相互转化, 同时公平重构协议还实现了Fairness. 非线性算子的安全计算协议在线阶段通信轮次均为常数轮. 从实验结果综合来看, Trident与ABY3相比具有明显的优势.

    References

    [1] P. Mohassel and P. Rindal, “ABY3: A Mixed Protocol Framework for Machine Learning,” in ACM CCS, 2018.


    本文标题: Trident: Efficient 4PC Framework for Privacy Preserving Machine Learning
    本文作者: 云中雨雾
    本文链接: https://weiviming.github.io/16524092173945.html
    本站文章采用 知识共享署名4.0 国际许可协议进行许可
    除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
    最后编辑时间: 2022-05-13T10:33:37+08:00