Secure Evaluation of Quantized Neural Networks

今天给大家带来的是发表于PoPETs'20上的文章Secure Evaluation of Quantized Neural Networks, 作者是来自丹麦Aarhus大学的Anders Dalskov, Daniel Escudero, Marcel Keller. 原文链接: 这里.

Introduction

目前在实践中进行安全推理的研究大多聚焦于提升性能, 但这是远远不够的. 从机器学习的角度来说, 大多数现有的安全推理方案依赖于专门的激活函数(如CryptoNets)或专门的训练过程(如XONN), 此外, 浮点数到定点数的转化、对激活函数的近似步骤, 所有这些都会影响模型的准确率, 从而影响模型的表达能力. 这成为开发机器学习方案时不得不考虑的一个问题. 从MPC的角度来说, 所使用的MPC对于被评估的网络来说应该是“Oblivious”的, 因为这将允许用户自由地选取适合他们的威胁模型, 而不需要考虑网络的结构或者专门的硬件. 本文研究了通用MPC框架是如何用来评估CNN的. 这篇文章提出并回答了以下两个问题:

主流的机器学习框架在多大程度上支持“MPC友好”模型而不需要定制转换协议? 换而言之, 是否可以使用标准框架设计一个模型通过安全协议高效地评估它, 而不改动模型本身呢?
现有的MPC框架在多大程度上对模型支持“开箱即用”? 换而言之, 能否使用通用MPC框架安全地评估机器学习模型?

文章对上述两个问题给出了肯定的回答, 并指出Tensorflow, PyTorch和MXNet支持的量化技术可以安全评估模型, 这种评估可通过通用MPC框架来执行. 实验部分从MPC的几个维度进行了广泛的基准测试, 并指出现有的机器学习框架和现有的MPC协议之间的鸿沟可能比先前已有工作中的隐含建议的小的多.

Quantization

文章采用的量化技术是来自于Jacob等人的方案¹, 虽然不是当前最佳技术, 但它在Tensorflow中有相关实现(TFLite), 便于进行安全评估和对比. 此外, 该方案便于MPC实现, 因为它简化了CNN的激活函数和算术运算, 尽管Jacob方案的初衷只是减小模型的规模, 但当MPC实现时, 由于模运算的存在, 并不能达到减小网络规模的效果. 更多量化技术的综述可以参考Guo的文章².

Quantization and De-Quantization

Jacob方案有两个变种, 一是8-bit整数, 二是16-bit整数. 本文中主要关注8-bit整数.

令$m\in\mathbb R, z\in[0,2^8)_\mathbb{Z}$. 考虑函数$\mathsf{dequant}_{m,z}:[0,2^8)_\mathbb Z\rightarrow\mathbb R$, $\mathsf{dequant}_{m,z}(x)=m\cdot(x-z)$. 该函数将离散区间$[0,2^8)_\mathbb Z$映射到连续区间$I=[-m\cdot z,m\cdot(2^8-1-z))$. $\mathsf{quant}_{m,z}$为该函数的逆函数. 定义$\alpha\in I$的量化为$\mathsf{quant}_{m,z}(\alpha')$, 这里的$\alpha'$是与$\alpha$最近的数, 使得$\alpha'$是$\mathsf{dequant}_{m,z}$的像, 由于是连续空间映射到离散空间, 因此由于舍入的原因, 连续区间的多个值可能映射到离散空间中相同的值. 如下图.

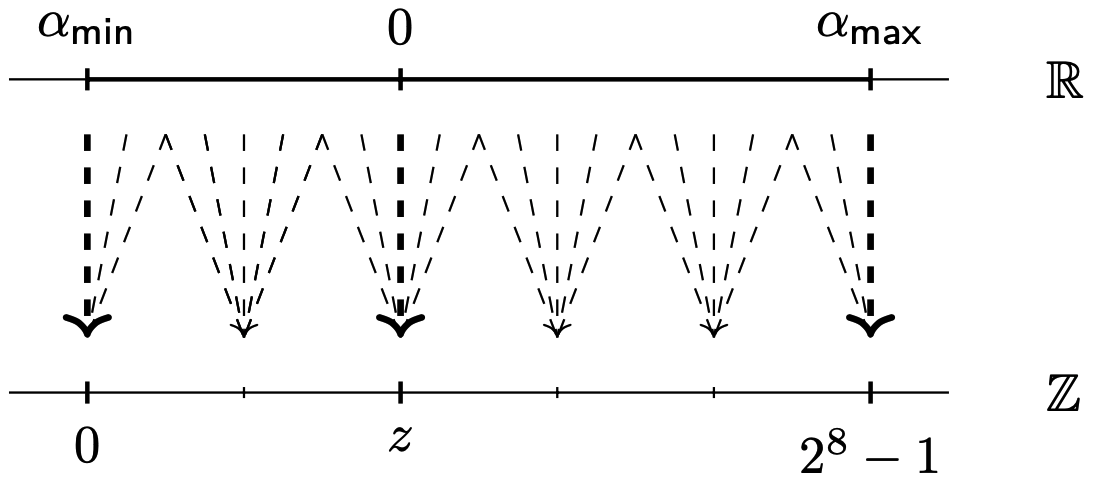
常数$m,z$称为量化参数, 其中$m$称为缩放因子(scale), $z$称为零点(zero point). 每个单独的张量$\mathbf{\alpha}$都有一对与之相关联的$m,z$. 这些参数是根据训练时记录给定张量的条目范围, 使得区间$[-m\cdot z,m\cdot(2^8-1-z))$足够大来容纳这些值来确定的.

Dot Products

下面介绍量化方案下的点积计算方案.

令$\alpha=(\alpha_1,\cdots,\alpha_N), \beta=(\beta_1,\cdots,\beta_N)$分别是量化参数为$(m_1,z_1), (m_2,z_2)$的两个向量. 令$\gamma=\sum_{i=1}^N\alpha_i\cdot\beta_i$, 量化参数为$(m_3,z_3)$. 令$c=\mathsf{quant}_{m_3,z_3}(\gamma), a_i=\mathsf{quant}_{m_1,z_1}(\alpha_i), b_i=\mathsf{quant}_{m_2,z_2}(\beta_i)$, 则可通过仅用整数算术和定点乘法从$a_i,b_i$计算$c$:

因为$\gamma\approx m_3(c-z_3), \alpha_i\approx m_1(a_i-z_1), \beta_i\approx m_2(b_i-z_2)$, 因此有

\[m_3\cdot(c-z_3)\approx\gamma=\sum_{i=1}^N\alpha_i\cdot\beta_i\approx\sum_{i=1}^N m_1\cdot(a_i-z_i)\cdot m_2\cdot(b_i-z_3). \]

于是, 我们可以得到$c$的近似为

\[c=z_3+\frac{m_1\cdot m_2}{m_3}\cdot\sum_{i=1}^N(a_i-z_1)\cdot(b_i-z_2). \]

其中, 求和$s=\sum_{i=1}^N(a_i-z_1)(b_i-z_2)$都是只有整数的算术运算, 但因为$m=\frac{m_1m_2}{m_3}$是实数, 因此$m\cdot s$不能通过只有整数的算术计算得出. TFLite中的处理方式是将$m$转化为定点数然后计算定点数乘法并舍入到与之最近的整数, 具体来说, 首先将$m$规范化(Normalized)为$m=2^{-n}m''$, 且将$m''$近似为$m''\approx2^{-31}m'$, 其中$m''\in[0.5,1)$, $m'$是个32bit的整数. 因为$m''\geq1/2$, 所以至少有30bit的相对精度. 于是, 我们便可以计算$m\cdot s$(最多64bit), 然后乘上$2^{-n-31}$以四舍五入到最近的整数, 最后加上$z_3$即可. 总结一下,

\[c=z_3+\lceil2^{-n-31}m's\rfloor. \]

若$\gamma$计算正确, 则$c$一定在区间$[0,2^8)_\mathbb{Z}$内, 但由于舍入误差的缘故, 实际情况可能并非如此. 因此, 前面步骤所得到的结果被限制(clamped)在区间$[0,2^8)_\mathbb{Z}$内.

CNN中需要计算偏置项(bias), 本文中bias的量化参数取$m=\frac{m_1m_2}{m_3}, z=0$, 便可以将其并入点积计算中.

Other Layers

本文不考虑其他激活函数. 对于ReLU, ReLU6, Maxpool层, 都是比较运算, 可以通过假设它们具有共同的量化参数, 从而在量化值上相对容易地实现, 因为若$\alpha=m(a-z), \beta=m(b-z)$, 则$\alpha\leq\beta$当且仅当$a\leq b$.

ReLU6这样的限制激活函数, 可以通过适当选取量化参数, 从而融入到点积计算中, 限制乘积在区间$[0,2^8)_\mathbb{Z}$内同时兼顾ReLU6的运算. 简而言之, 若$z=0, m=6/255$, 则可以保证对于任意的$q\in\{0,\cdots,2^8-1\}$, 有$m(q-z)\in[0,6]$.

Jacob的量化方案已经将量化神经网络的大多数运算变成了加法和乘法, 而这便于MPC协议的设计.

Quantized CNNs in MPC

System and Threat Model

基本场景: 服务器代理模式/客户-服务器模式(Client-server, CS), 模型拥有方和客户分别秘密共享模型和数据并外包到两个/三个服务器中, 由服务器通过给定输入执行安全多方计算协议运行安全推理任务, 并将分类结果发给所需参与方. 这里的服务器数量取决于共谋假设, 并允许至多一个服务器被腐化, 即两个服务器对应于不诚实大多数, 三个服务器对应于诚实大多数.

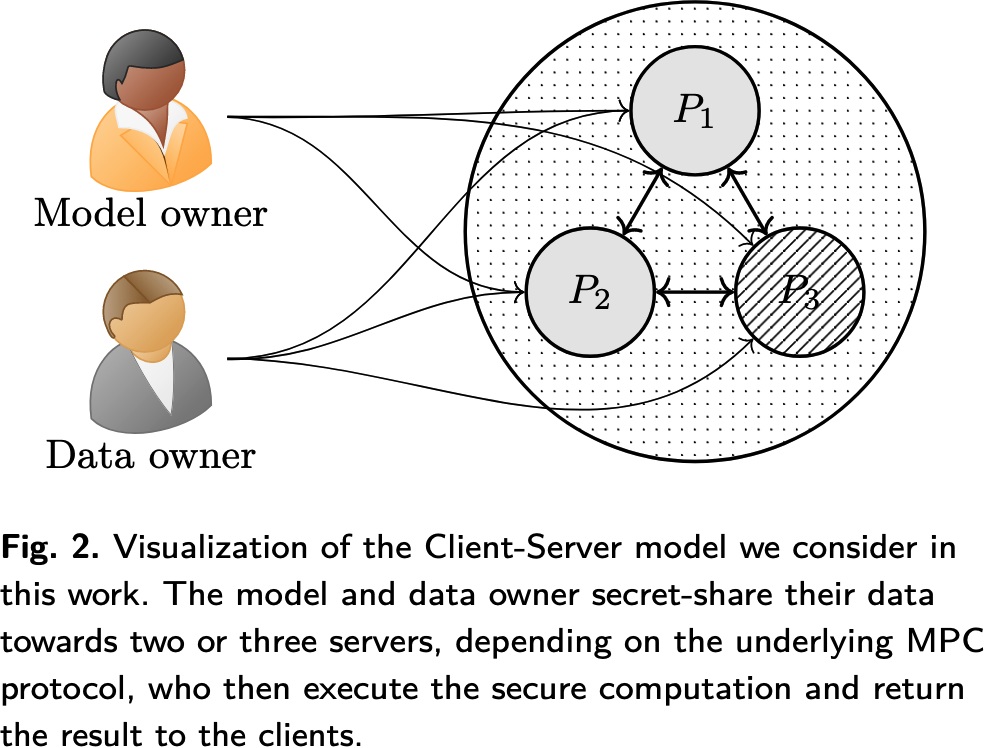
CS模型的另一个优点是高度兼容反应式计算(reactive computation), 这里预测的输出需要用于后续计算, 这种情况下, 由于服务器获得了输出的份额, 因此可以直接将此结果传输到另一个MPC计算任务中. 此外还可以考虑点对点模式, 但需要额外的一轮输入来保证输入的一致性.

本文中使用的通用MPC协议可以根据三个不同的维度进行分类:

腐化门限: 不诚实大多数(2PC) vs 诚实大多数(3PC);
腐化类型: 被动敌手 vs 主动敌手;
底层代数结构: $\mathbb F_p$ vs $\mathbb Z_{2^k}$.

实际应用时, 根据上述维度的不同, 采用的协议如表1所示.

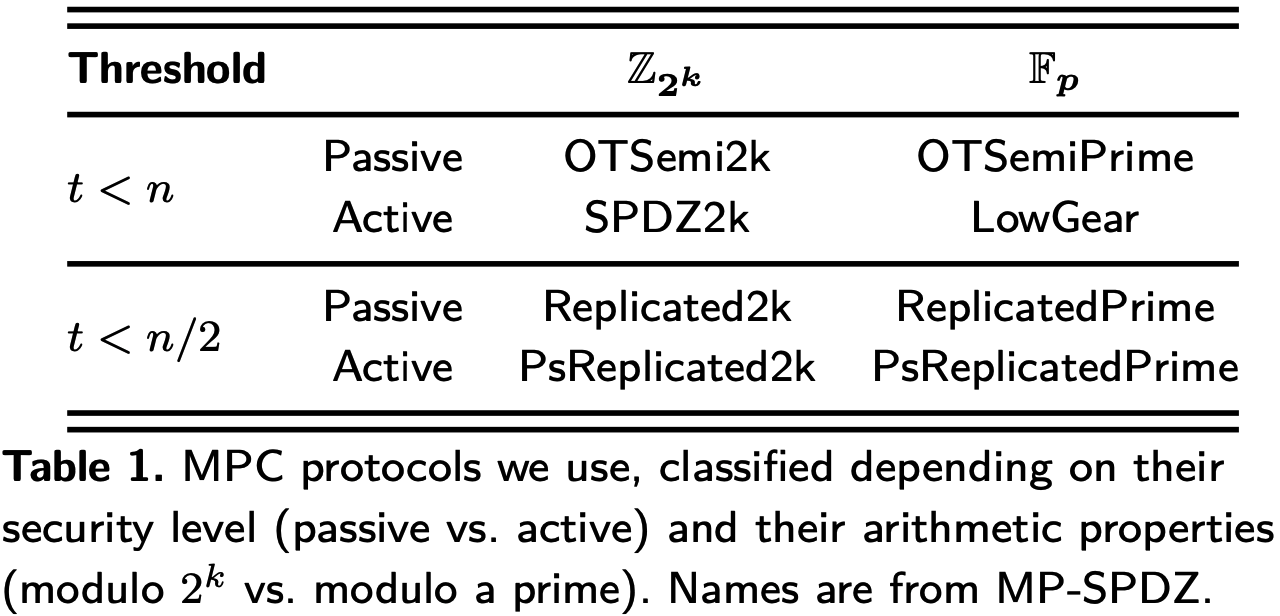
不诚实大多数: 不诚实大多数协议通常基于加法秘密共享和使用验证标签(authentication tags)来实现主动安全.
- $\mathsf{SPDZ2k}$: 二次幂环$\mathbb Z_{2^k}$上的第一个不诚实大多数设定下的主动安全协议, 可视为$\mathsf{MASCOT}$的扩展版本, 最早由Cramer等人在CRYPTO'18上提出³, 由Damgård等人⁴首先实现. 乘法计算依赖于预处理基于OT来生成Beaver triples, 验证方案同SPDZ, 但是是在$\mathbb{Z}_{2^{k+s}}$上进行验证. 为了一个检验Beaver triple的正确性, 通常需要"献祭"(Sacrifice)另一个Beaver triple.
- $\mathsf{OTSemi2k}, \mathsf{OTSemiPrime}$: 分别是$\mathsf{SPDZ2k}$和$\mathsf{MASCOT}$的精简版本, 没有验证标签和"献祭"步骤. 基于OT来生成Beaver triples.
- $\mathsf{LowGear}$: Keller等人提出的素数域上主动安全协议, 基于LWE的半同态加密方案⁵.
诚实大多数: 诚实大多数协议通常基于Shamir秘密共享(适用于任意数量参与方的情况)和复制秘密共享(Replicated Secret Sharing, 适用于参与方数量较少的情况)来进行设计. 本文的场景下, 计算方数量较少, 使用复制秘密共享即可.
- $\mathsf{Replicated2k}, \mathsf{ReplicatedPrime}$: 当前最高效的被动安全乘法协议是由Araki等人在CCS'16年提出的方案⁶, 仅需通信3个元素.
- $\mathsf{PsReplicatedPrime}$: Lindell和Nof将$\mathsf{ReplicatedPrime}$扩展到主动安全的协议⁷, 通过预处理可能不正确的三元组用于在线阶段, 并在协议执行结束后通过"献祭"技术检查它们的正确性来实现主动安全.
- $\mathsf{PsReplicated2k}$: 由Eerkison等人提出的协议⁸, 是上面Lindell等人方案在二次幂环$\mathbb Z_{2^k}$上的扩展版本.

Secure Comparison

安全计算$\langle b\rangle\leftarrow\langle x\rangle<_?\langle y\rangle$, 其中比特$b=(x<y)$. 对于不同的代数结构, $\mathbb F_p$可参考文献⁹; $\mathbb Z_{2^k}$可参考文献⁴. 对于复制秘密共享, ABY3提供了更高效的方案.

Truncation

对于公开参数$m$, 需要安全计算$\langle y\rangle\leftarrow\langle x\rangle$, 这里的$y=\lfloor\frac{x}{2^m}\rfloor$. 可通过概率截断(probabilistic truncation)协议. 在概率截断协议中, 计算$\langle z\rangle$, 其中$z=\lfloor\frac{x}{2^m}\rfloor+u$, 这里$u\in\{0,1\}$是小误差, 取值取决于$\lfloor\frac{x}{2^m}\rceil$, 即$u=1$的概率为$\frac{x}{2^m}$的小数部分$(x\bmod2^m)/2^m$. 例如$x=7,m=2$, 则概率截断将以$(7\bmod2^2)/2^2=0.75$的概率输出$u=1, z=\lfloor\frac{7}{4}\rfloor+1=2$, 以0.25的概率输出$u=0, z=\lfloor\frac{7}{4}\rfloor=1$.

本文提出了一种环$\mathbb Z_{2^k}$上的概率截断方案, 份额只需比秘密大1bit, 同时常数轮通信的, 结果的误差最多为1,偏向于最接近$x/2^m$的整数. 假设有一个生成随机份额比特的方法, 生成$\langle b\rangle$, 满足$b\in\{0,1\}$是均匀随机且敌手未知的. 在不诚实大多数设定下可以参考文献⁴的方法生成. 一般地, 可以让$P_i$生成1比特$\langle b_i\rangle$, 然后参与方将这些比特XOR在一起得到一个随机1比特. 当然为了确保$P_i$生成的$\langle b_i\rangle$确实是1比特的, 可以验证$\langle b_i\rangle\cdot(1-\langle b_i\rangle)$是否为零. 具体的概率截断如下, 注意图中第二步应为$c'\leftarrow (c\bmod2^{k-1})/2^m$, 第四步中应为输出$c'-\sum_{i=m}^{k-2}\langle r_i\rangle\cdot2^{i-m}+\langle b\rangle\cdot2^{k-m-1}$.

如果考虑环$\mathbb Z_{2^k}$上三方复制秘密共享、半诚实安全设定, 可以让将上述对称的三方协议转化为两方协议, 由第三方生成供其他两方使用的相关随机性, 如任意长度的随机数, 这样不再需要逐比特生成随机数.

由于量化方案与传统定点算术不同, 量化方案中的参数是针对网络的特定层自适应选取的, 这些参数是模型的敏感信息, 因此有必要探索当$m$是秘密时的截断方案. 假设$M$是$m$的公开上界, 首先对$M-m$比特分解, 根据$M-m=\sum_{i}2^i\cdot b_i$, 我们得到$b_i$的份额$\langle b_i\rangle$, 并计算$\langle 2^{M-m}\rangle=\prod_i(1+\langle b_i\rangle\cdot(2^{2^i}-1))$. 特别地, 在CS模型下, $m$为模型拥有方Client所知, 可以简单地认为Client分发了$\langle 2^{M-m}\rangle$, 不需要进行比特分解. 接着, 计算$\langle 2^{M-m}\rangle\cdot\langle x\rangle$, 并将其结果用上述截断公开值的方案截断$M$位即可. 如下图, 得到的$y=\lfloor \frac{2^{M-m}x}{2^M}\rfloor=\lfloor\frac{x}{2^m}\rfloor$. 注意, 这个方案需要确保$2^{M-m}\cdot x$不会溢出, 即必须保证$(M-m)+\log_2(|x|)<|Modulus|$成立, 这里的$|Modulus|$表示模数比特长度.

Putting it all Together

假设模型拥有者拥有量化CNN的所有参数信息, 并通过秘密共享方案分发网络每一层的量化权重、偏置项给服务器(注意虽然明文只有8bits, 但份额有64bits), 与每个张量相关联的零点也被分享给各参与方.

下面来计算公式(2). 计算方(服务器)有零点$z_1,z_2,z_3$的份额, 量化输入$a_i,b_i$, 整数缩放因子$m'$和幂$2^{L-\ell}$, 这里的$\ell=n+31, 2^{-n-31}\cdot m'\approx m=(m_1\cdot m_2)/m_3$, 且$L$是$\ell$的上界. 为了计算公式(2), 计算方首先计算点积$\langle s\rangle=\sum_{i=1}^N(\langle a_i\rangle-\langle z_1\rangle)\cdot(\langle b_i\rangle-\langle z_2\rangle)$, 然后通过乘法协议计算$\langle m\cdot s\rangle=\langle m\rangle\cdot\langle s\rangle$, 并通过$\mathsf{TruncPriv}$协议从$\langle 2^{L-\ell}\rangle$和$\langle m\cdot s\rangle$计算$\lfloor 2^{-n-31}\cdot(m\cdot s)\rceil$的份额, 然后计算$\lfloor 2^{-m}\cdot x\rceil=\lfloor2^{-m}\cdot x+0.5\rfloor=\lfloor 2^{-m}\cdot (x+2^{m-1})\rfloor$进行舍入计算, 最后本地加上$\langle z_3\rangle$, 限制$\langle x\rangle$到区间$[0,2^8)$, 这可根据安全比较, 将$\langle x\rangle$与边界0和255进行比较, 结合不经意选取来达到: 若$s\in\{0,1\}$, 则对任意的$a_0,a_1$, 则$a_s=s\cdot(a_1-a_0)+a_0$.

平均池(Average pooling)计算中涉及的除法可以通过Goldschmidt's算法来计算, 安全计算协议可以参考Catrina和Saxena的这篇文献¹⁰. 最大池(Max pooling)要求计算的max函数可通过安全比较协议来实现.

在获得输出向量的份额后, 为了避免在计算SoftMax等激活函数之前向秘密拥有方/数据拥有方揭示向量本身, 本文中采用的方案是计算输出数组的arg max, 并返回最有可能的标签的索引来替代$e^x$, 因为幂运算是个单调递增函数. 例如, 在SecureML中, 将SoftMax函数中的幂替换为ReLU, 即用$\mathsf{ReLU}(x)$替代$e^x$. 此外, 还存在更多MPC友好的解决方案, 例如在spherical Softmax中将$e^x$替换为$x^2$.

Implementation and Benchmarking

本文的实验部分评估的是MobileNets类型架构的神经网络, 它包含28层, 1000个输出类, 在ImageNet数据集上进行训练, 在TensorFlow存储库上可用的预训练模型和准确率进行评估.

安全推理方面, 使用MP-SPDZ框架进行实现, 计算域分别为128bits的素数域和72bits的二次幂环, 因为需要额外的空间确保秘密截断是正确的. 实验代码已经发布在MP-SPDZ框架中, 脚本和图像见这里.

CNN核心运算是卷积, 效率提升主要来源于点积和乘法总数, 两者定量实验结果表2. 点积的通信开销取决于项的数量.

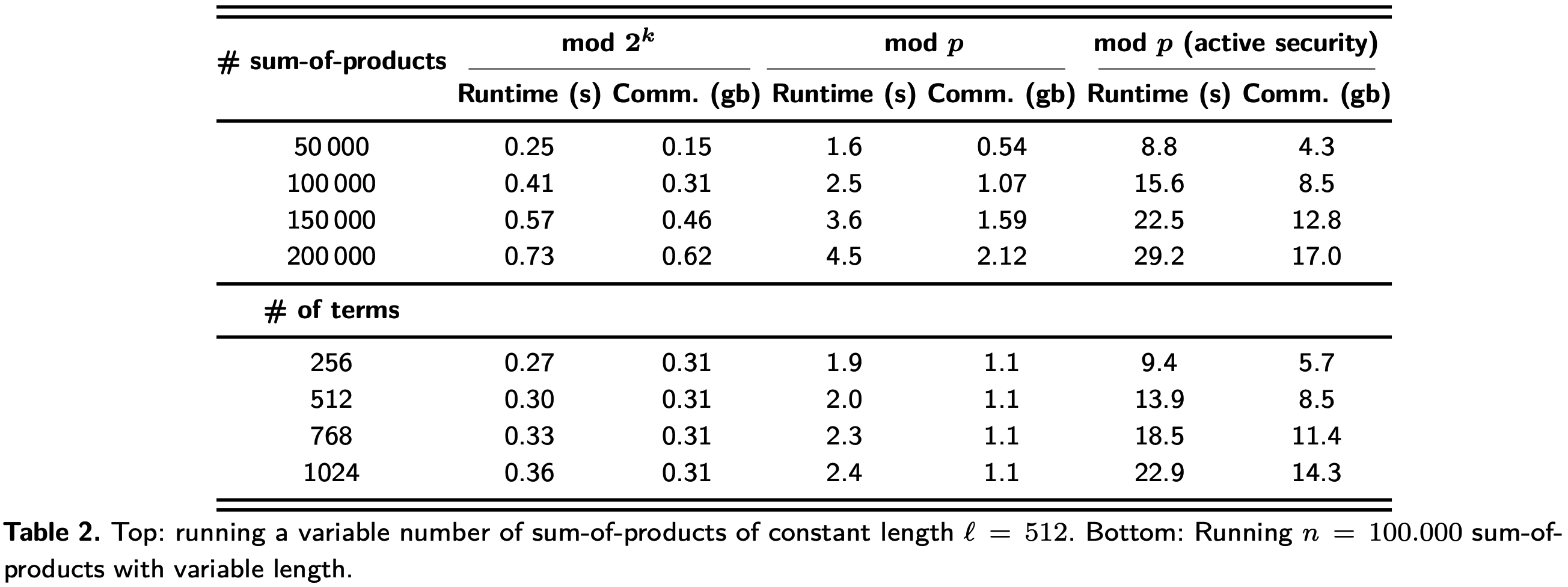
表3展示了16个预训练的V1 MobileNet模型分别从腐化门限(诚实大多数 VS 不诚实大多数)、腐化模型(被动 VS 主动)、代数结构($\mathbb{F}_p$ VS $\mathbb Z_{2^k}$)、截断类型(Probabilistic truncation VS Nearest rounding)4个不同维度的运行时间的评估结果.

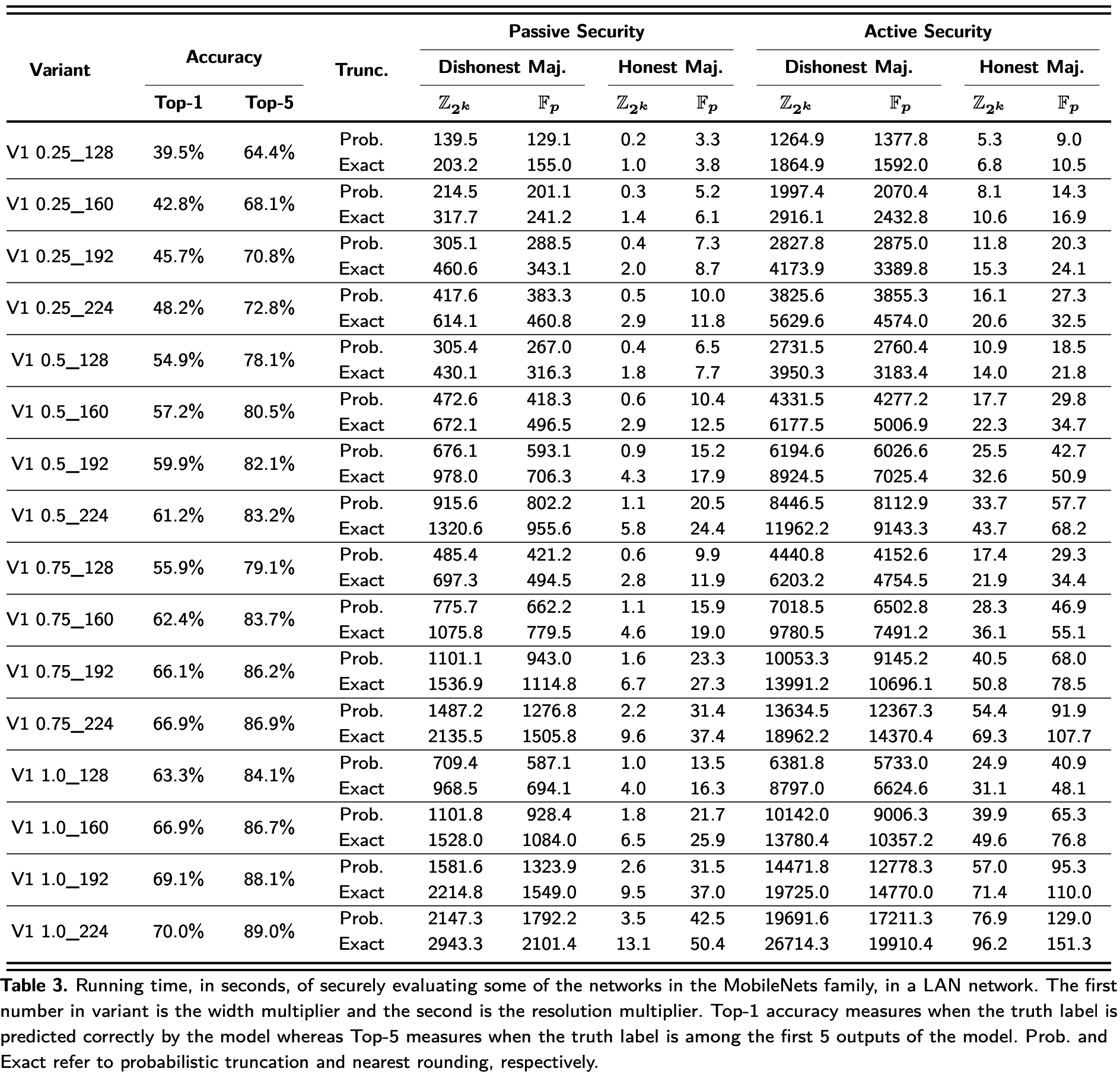
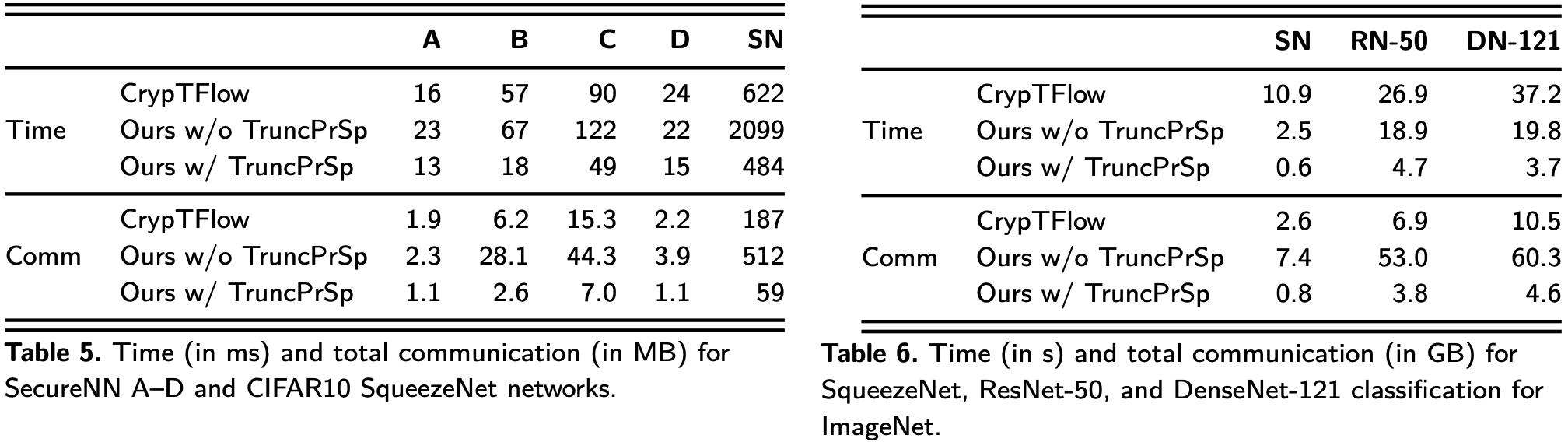
图3和图4分别是诚实大多数协议和不诚实大多数协议的实验结果.

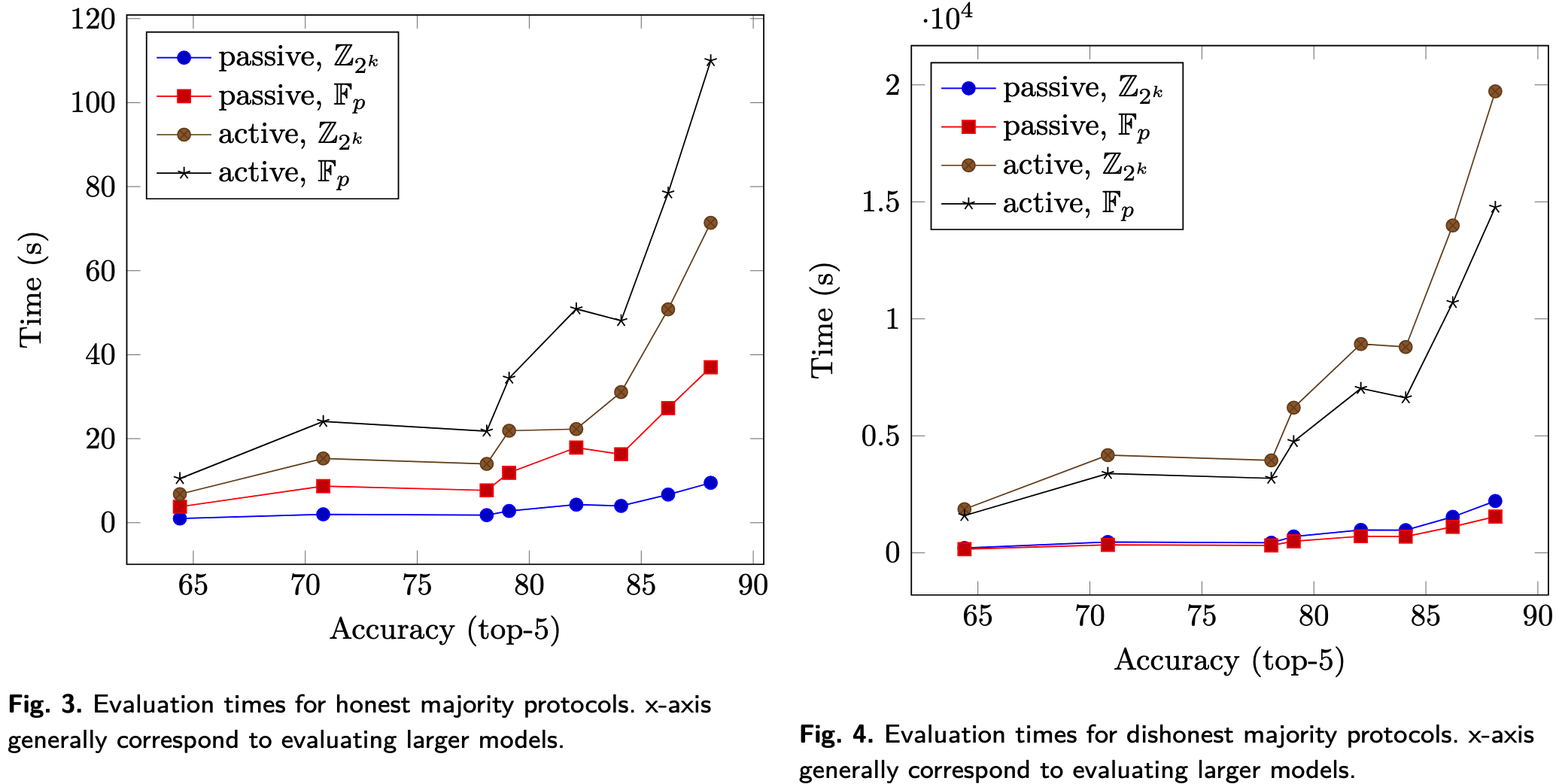
表4展示了在最简网络下, 对于三方以上的协议, 扩展到最多五方的实验结果. 腐化方的数量在诚实大多数中被设定为1、1、2, 在不诚实大多数中被设定为2、3、4.

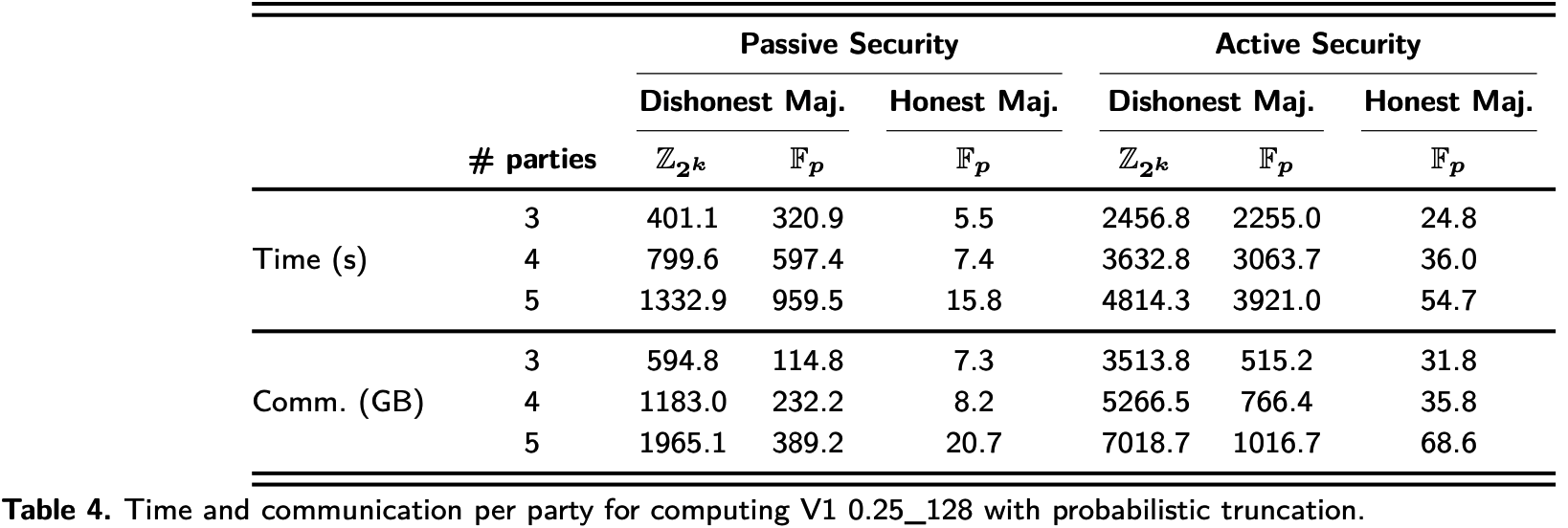
本文提出的特殊截断协议不对秘密进行任何限制, 但CrypTFlow中要求秘密的前$s$比特为零, 这里的$s$是统计安全参数. 表5展示的是相同网络设置下, 不同截断方案的实验结果. 表6展示了使用特殊截断实现和不使用特殊截断实现的CrypTFlow的ImageNet测试结果, 注意这里的结果取自不同框架下的最优线程, MP-SPDZ为32线程, CrypTFlow为8线程.

LAN网络下通信量(GB)测试结果如下:

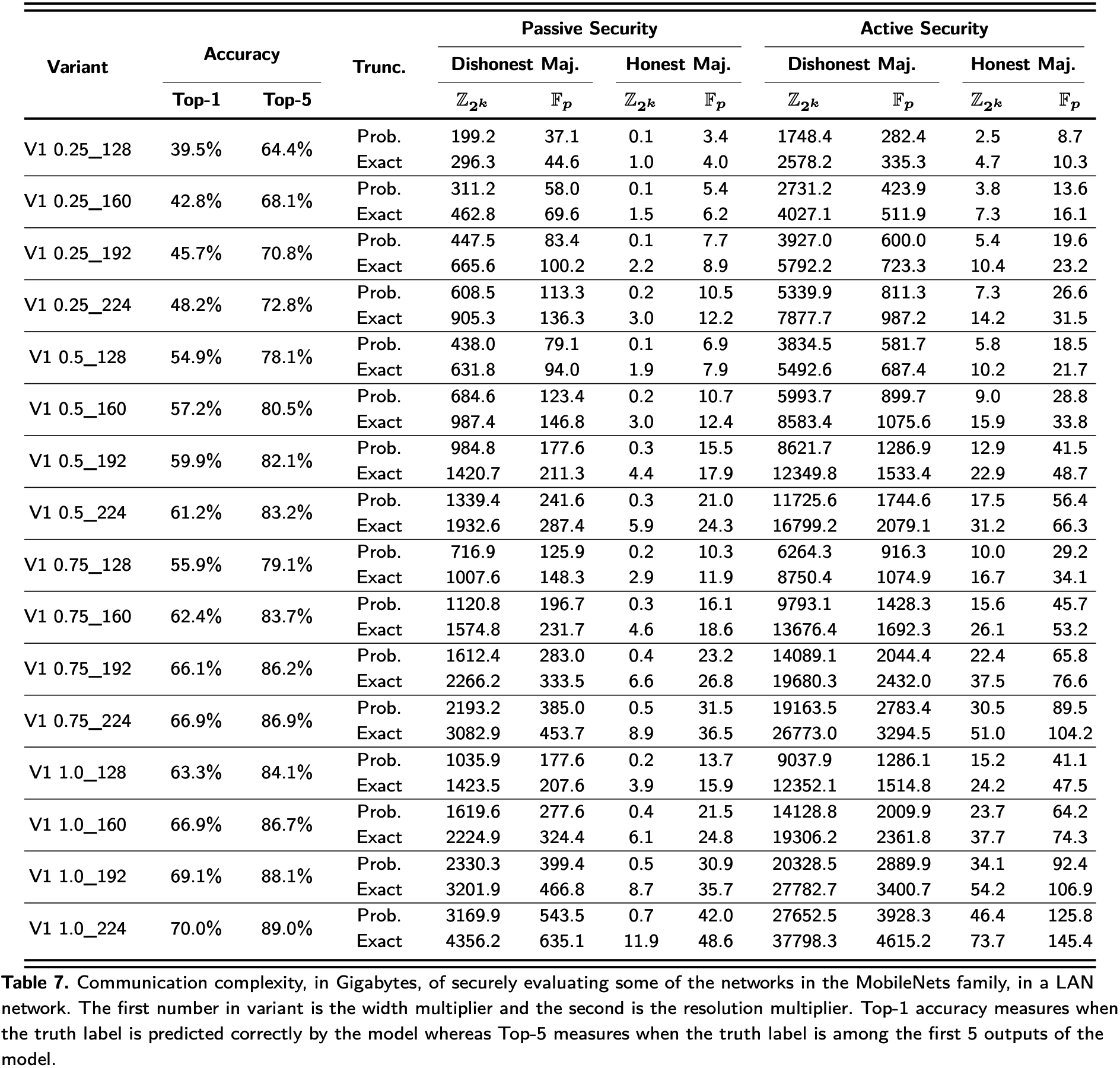
总的来说, 实验部分的关键结论如下:

由于不诚实大多数协议需要昂贵的预处理, 因此相同条件下从诚实大多数转移到不诚实大多数的开销差距高达200倍以上.
不同腐化模型之间的转移相对便宜, 不管腐化门限如何, 从被动安全到主动安全只增加了3-30倍的推理时间.
对于不同的代数结构来说, 基于环的大多数协议在被动安全设定下优于基于有限域的协议, 而在主动安全设定下则相反.
使用概率截断方案可以加快推理速度, 但这种效率提高以可能存在的模型精度下降为代价, 对于更深的模型会更加明显.

Conclusions

本文验证了使用现有MPC协议在不修改机器学习模型的前提下, 安全评估大型、现实的神经网络是可行的. 本文中评估的神经网络是未经修改的, 可通过标准Tensorflow或任何支持量化类型的框架(如PyTorch和MXNet)进行训练. 对于用户而言, 通用MPC足以对网络进行评估, 用户可以从更广泛的威胁模型中自由选择; 此外, 即使模型设计者对安全框架一无所知, Tensorflow输出的模型也可以在不经修改的情况下进行评估. 如果想在预测精度和效率方面进行权衡, 那么专用协议可能是更好的选择, 例如文章中提出的概率截断协议等.

References

Benoit Jacob, Skirmantas Kligys, Bo Chen, Menglong Zhu, Matthew Tang, Andrew G. Howard, Hartwig Adam, and Dmitry Kalenichenko. Quantization and training of neural networks for efficient integer-arithmetic-only inference. CoRR, abs/1712.05877, 2017. ↩

Yunhui Guo. A survey on methods and theories of quantized neural networks. arXiv preprint arXiv:1808.04752, 2018. ↩

Ronald Cramer, Ivan Damgård, Daniel Escudero, Peter Scholl, and Chaoping Xing. SPD Z2k : Efficient MPCmod 2k for dishonest majority. In Hovav Shacham and Alexandra Boldyreva, editors, Advances in Cryptology – CRYPTO 2018, Part II, volume 10992 of Lecture Notes in Computer Science, pages 769–798, Santa Barbara, CA, USA, August 19–23, 2018. Springer, Heidelberg, Germany. ↩

I. Damgård, D. Escudero, T. Frederiksen, M. Keller,P. Scholl, and N. Volgushev. New primitives for actively secure mpc over rings with applications to private machine learning. In 2019 2019 IEEE Symposium on Security and Privacy (SP), pages 1325–1343, Los Alamitos, CA, USA, may 2019. IEEE Computer Society. ↩ ↩² ↩³
Marcel Keller, Valerio Pastro, and Dragos Rotaru. Over- drive: Making SPDZ great again. In Jesper Buus Nielsen and Vincent Rijmen, editors, Advances in Cryptology – EUROCRYPT 2018, Part III, volume 10822 of Lecture Notes in Computer Science, pages 158–189, Tel Aviv, Israel, April 29 – May 3, 2018. Springer, Heidelberg, Germany. ↩

Toshinori Araki, Jun Furukawa, Yehuda Lindell, Ariel Nof, and Kazuma Ohara. High-throughput semi-honest secure three-party computation with an honest majority. In Edgar R. Weippl, Stefan Katzenbeisser, Christopher Kruegel, An- drew C. Myers, and Shai Halevi, editors, ACM CCS 2016: 23rd Conference on Computer and Communications Security, pages 805–817, Vienna, Austria, October 24–28, 2016. ACM Press. ↩

Yehuda Lindell and Ariel Nof. A framework for constructing fast MPC over arithmetic circuits with malicious adversaries and an honest-majority. In Bhavani M. Thuraisingham, David Evans, Tal Malkin, and Dongyan Xu, editors, ACM CCS 2017: 24th Conference on Computer and Communications Security, pages 259–276, Dallas, TX, USA, October 31 – November 2, 2017. ACM Press. ↩

Hendrik Eerikson, Marcel Keller, Claudio Orlandi, Pille Pullonen, Joonas Puura, and Mark Simkin. Use your brain! Arithmetic 3PC for any modulus with active security. In 1st Conference on Information-Theoretic Cryptography (ITC 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020. ↩

Octavian Catrina and Sebastiaan de Hoogh. Improved primitives for secure multiparty integer computation. In Juan A. Garay and Roberto De Prisco, editors, SCN 10: 7th Interna- tional Conference on Security in Communication Networks, volume 6280 of Lecture Notes in Computer Science, pages 182–199, Amalfi, Italy, September 13–15, 2010. Springer, Heidelberg, Germany. ↩

Octavian Catrina and Amitabh Saxena. Secure computation with fixed-point numbers. In Radu Sion, editor, FC 2010: 14th International Conference on Financial Cryptography and Data Security, volume 6052 of Lecture Notes in Com- puter Science, pages 35–50, Tenerife, Canary Islands, Spain, January 25–28, 2010. Springer, Heidelberg, Germany. ↩

本文标题: Secure Evaluation of Quantized Neural Networks
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16519051511907.html
本站文章采用知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间: 2022-05-07T14:32:31+08:00