云中雨雾

    BLAZE: Blazing Fast Privacy-preserving Machine Learning

    2022/03/20 23:27 下午 标签: #隐私保护机器学习

    今天给大家带来的是Arpita Patra等人发表于NDSS'20上的文章《BLAZE: Blazing Fast Privacy-preserving Machine Learning》, 论文链接: https://arxiv.org/pdf/2005.09042.pdf.

    摘要

    本文提出的BLAZE是安全外包三服务器服务环境下可抵抗一个恶意敌手的环\(\mathbb Z_{2^\ell}\)上的PPML框架, 实现了公平性(当敌手获得输出时, 所有诚实参与方也能获得相同的输出). 利用独立于输入的预处理阶段, BLAZE基于输入的在线阶段非常高效, 主要原因在于:

    • 提出的3PC诚实大多数假设下在线阶段通信量与向量长度无关的恶意点积计算协议;
    • 不需要像ABY3一样借助Ripple Carry Adders(RCA)来构造协议.
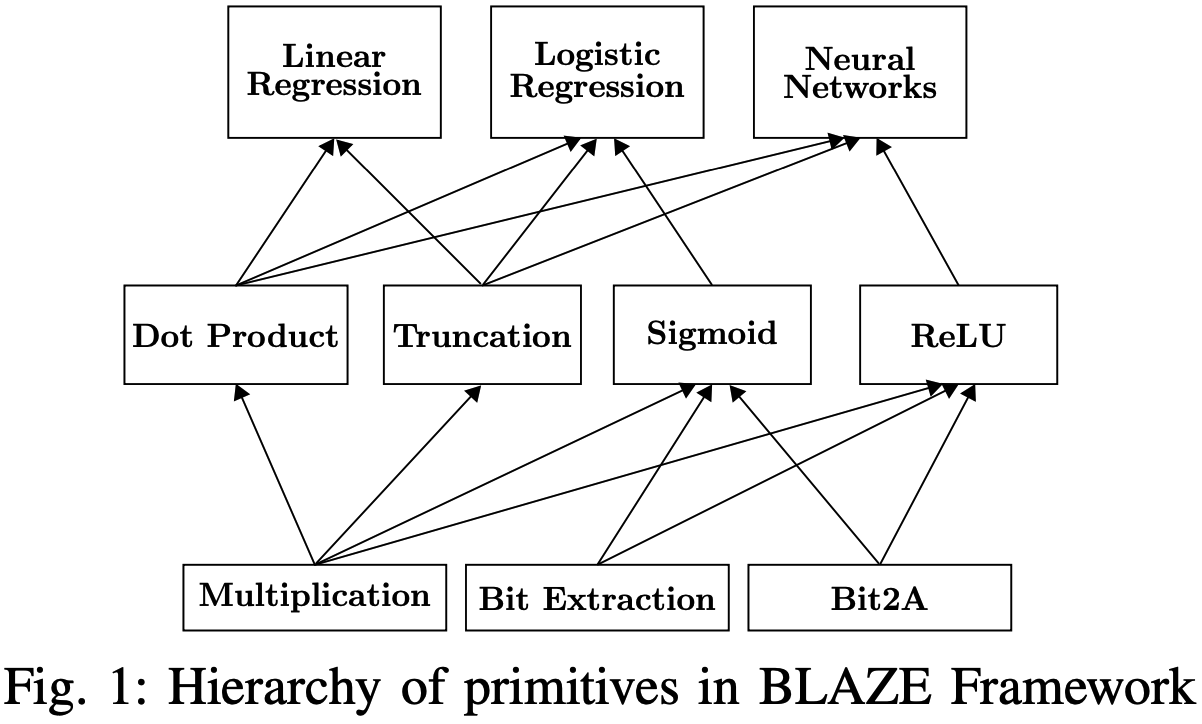
    image-20220319170717589

    基础知识

    安全模型与符号约定

    三服务器代理模式, 静态敌手至多腐化一个服务器. 为减少通信开销, 服务器之间通过一次性密钥设置生成预共享密钥, 通过伪随机生成函数(PRF)来生成关联随机性. 抗碰撞的Hash函数记为\(\mathsf H()\), 承诺记作\(\mathsf{Com}()\). 计算域为\(\mathbb Z_{2^\ell}=\mathbb Z_{2^{64}}, \mathbb Z_{2^1}\), 分别代表算术环和布尔环.

    秘密共享语义

    • \([\cdot]\)秘密共享: 秘密\(v\)在\(P_1\)和\(P_2\)两方下的加法秘密共享, \(P_1\)有\([v]_1\), \(P_2\)有\([v]_2\), 使得\(v=[v]_1+[v]_2\).
    • \(\langle\cdot\rangle\)秘密共享: 秘密\(v\)在三方下的秘密共享, (1)存在\([\lambda_v]_1,[\lambda_v]_2\in\mathbb Z_{2^\ell}\), 使得\(\lambda_v=[\lambda_v]_1+[\lambda_v]_2\), (2)\(P_0\)的份额为\(([\lambda_v]_1,[\lambda_v]_2)\), \(P_1\)的份额为\(([\lambda_v]_1,v+\lambda_v)\), \(P_2\)的份额为\(([\lambda_v]_2,v+\lambda_v)\).
    • \([\![\cdot]\!]\)秘密共享: 秘密\(v\)在三方下的秘密共享, (1)\(v\)在\(\langle\cdot\rangle\)秘密共享, 即\(P_0\)有\(([\alpha_v]_1,[\alpha_v]_2)\), \(P_1\)有\(([\alpha_v]_1,\beta_v)\), \(P_2\)有\(([\alpha_v]_2,\beta_v)\), 其中\(\beta_v=v+\alpha_v\), \(\alpha_v=[\alpha_v]_1+[\alpha_v]_2\), (2) 存在\(\gamma_v\in\mathbb Z_{2^\ell}\), 使得\(P_1,P_2\)有\(\gamma_v\), 同时\(P_0\)有\(\beta_v+\gamma_v\).

    以上三种秘密共享可以总结为

    image-20220319195925412

    由于三种秘密共享方案都是线性的, 因此加法和标量积的计算不需要交互. 此外, 容易看出任意两方通过交换对方所缺失的份额都可以重构出原始秘密\(v\).

    基本协议构造

    秘密共享协议

    秘密共享协议\(\Pi_\mathsf{sh}(P_i,v)\): 允许\(P_i\)生成\(v\)的\([\![\cdot]\!]\)份额. 总体思路是预处理阶段参与方使用预共享密钥生成部分份额, 然后在线阶段参与方发送没有的份额发送给其他两方参与方以满足秘密共享语义, 通过交换接收到的份额的hash值来判断两方收到的秘密份额是否一致, 若一致, 则参与方接受该份额, 否则直接中止协议(abort), 具体协议过程如下:

    image-20220319200924679

    联合共享协议

    联合共享协议\(\Pi_\mathsf{jsh}(P_i,P_j,v)\): 允许两个参与方\(P_i,P_j\)联合生成他们的共同秘密\(v\)的\([\![\cdot]\!]\)份额\([\![v]\!]\). 总体思路是\(P_i\)执行秘密共享协议\(\Pi_\mathsf{sh}(P_i,v)\)生成\([\![v]\!]\), \(P_j\)负责验证\(P_i\)生成的份额的正确性, 即发送份额的hash值给接收方进行验证一致性. 根据两方的不同可以分为三种情况, 具体协议过程如下:

    image-20220319204146055

    若预处理阶段\(P_i\)和\(P_j\)都知道\(v\), 则可以不需要交互生成\([\![v]\!]\), 具体方法是将相应份额设定为下表形式, 由于联合共享中的两方都知道秘密, 而其中至少一方是诚实的, 因此这样做是安全的.

    image-20220319205207743

    秘密重构协议

    秘密重构协议\(\Pi_\mathsf{rec}(\mathcal P,[\![v]\!])\): 允许\(\mathcal P\)中的参与方从\([\![v]\!]\)中重构秘密\(v\). 一方发送所缺失的份额给另一方, 第三方发送份额的hash值进行验证一致性, 若验证通过则可以重构秘密\(v\). 具体协议过程如下图4所示.

    在外包场景中, 当要向用户\(P\)重构\(v\)时, \(P_0\)发送\(([\![\alpha_v]\!]^\mathbf A, \mathsf{H}([\![\alpha_v]\!]^\mathbf B))\), \(P_1\)发送\((\beta_v, \mathsf{H}([\![\alpha_v]\!]^\mathbf A))\), \(P_2\)发送\(([\![\alpha_v]\!]^\mathbf B, \mathsf{H}(\beta_v))\), \(P\)验证相应的hash值是否匹配, 若匹配则接受, 否则中止.

    image-20220319210736130

    公平重构协议\(\Pi_\mathsf{frec}(\mathcal P,[\![v]\!])\): 确保参与方\(\mathcal P\)公平地重构秘密\(v\), 这意味着当腐化方获得\(v\)时保证诚实参与方也能得到相同的\(v\). 具体实现原理与ASTRA相同, 都是通过承诺来完成, 协议过程如下:

    frecp

    秘密乘法协议

    秘密乘法协议\(\Pi_\mathsf{mult}(\mathcal P,[\![x]\!],[\![y]\!])\): 允许\(\mathcal P\)计算\(z=xy\)的秘密份额\([\![z]\!]\).

    为此, 先介绍半诚实安全模型下的秘密乘法协议: 在预处理阶段, \(P_0, P_1\)随机选取\([\alpha_z]_1\), \(P_0,P_2\)随机选取\([\alpha_z]_2\), \(P_1,P_2\)随机选取\(\gamma_z\). 然后\(P_0\)本地计算\(\Gamma_{xy}=\alpha_x\alpha_y\)并生成它在\(P_1,P_2\)之间的\([\cdot]\)份额. 因为

    \[\begin{aligned} \beta_z&=z+\alpha_z=xy+\alpha_z=(\beta_x-\alpha_x)(\beta_y-\alpha_y)+\alpha_z\\ &=\beta_x\beta_y-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z, \end{aligned}\tag{1} \]

    成立, 因此在在线阶段对于\(j\in\{1,2\}\), \(P_j\)可以本地计算\([\beta_z]_j=(j-1)\beta_x\beta_y-\beta_x[\alpha_y]_j-\beta_y[\alpha_x]_j+[\Gamma_{xy}]_j+[\alpha_z]_j\), 相互交换份额重构\(\beta_z\), 最后\(P_1\)计算并发送\(\beta_z+\gamma_z\)给\(P_0\), 完成半诚实安全下的秘密乘法计算. 正确性由公式\((1)\)保证.

    但在恶意安全模型下, 上述秘密乘法协议存在如下三个问题:

    1. 当\(P_0\)是腐化方时, 预处理阶段\(P_0\)生成\(\Gamma_{xy}\)的\([\cdot]\)份额可能是错误的, 即\(\Gamma_{xy}\neq\alpha_x\alpha_y\);
    2. 当\(P_1\)或\(P_2\)是腐化方时, 在线阶段发送给另一方的\(\beta_z\)的份额\([\beta_z]_j\)可能是错误的, 从而导致重构的\(\beta_z\)是错误的;
    3. 当\(P_1\)是腐化方时, 在线阶段发送给\(P_0\)的值\(\beta_z+\gamma_z\)是错误的.

    问题1和问题2可以规约到验证Beaver triple的正确性问题. 对于问题3, 为了验证\(P_1\)发送的\(\beta_z+\gamma_z\)的正确性, 只需\(P_2\)计算它的hash值并发送给\(P_1\)进行验证一致性, 若不然则中止.

    下面解决问题2, \(P_0\)通过\(\beta_x^*=\beta_x+\gamma_x\)和\(\beta_y^*=\beta_y+\gamma_y\), 可计算\(\beta_z^*=-\beta_x^*\alpha_y-\beta_y^*\alpha_x+2\Gamma_{xy}+\alpha_z\). 令\(\chi=\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi\), 则\(\beta_z^*\)可以写成如下形式:

    \[\begin{aligned} \beta_z^*&=-\beta_x^*\alpha_y-\beta_y^*\alpha_x+2\Gamma_{xy}+\alpha_z\\ &=-(\beta_x+\gamma_x)\alpha_y-(\beta_y+\gamma_y)\alpha_x+2\Gamma_{xy}+\alpha_z\\ &=(-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy})\\ &=(\beta_z-\beta_x\beta_y)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi)+\psi\\ &=(\beta_z-\beta_x\beta_y+\psi)-\chi. \end{aligned} \]

    设\(P_1,P_2\)共同选取随机数\(\psi\in\mathbb{Z}_{2^\ell}\). 若\(P_0\)已知\(\chi\), 则可以发送\(\beta_z^*+\chi\)给\(P_1,P_2\). 然后\(P_1,P_2\)通过使用\(\beta_x,\beta_y\)和\(\chi\), 可以计算\(\beta_z-\beta_x\beta_y+\psi\overset{?}{=}\beta_z^*+\chi\)来验证\(\beta_z\)的正确性. 于是, 关键在于如何让\(P_0\)得到\(\chi\).

    对\(j\in\{1,2\}\), 设\([\psi]_j\)是\(P_1,P_2\)使用预共享密钥本地生成的随机数, \(P_j\)可以本地计算\([\chi]_j=\gamma_x[\alpha_y]_j+\gamma_y[\alpha_x]_j-[\Gamma_{xy}]_j+[\psi]_j\). \(P_j\)可发送各自的\([\chi]_j\)给\(P_0\), 从而\(P_0\)可以重构出\(\chi=[\chi]_1+[\chi]_2\). 为了验证\(P_0\)正确地计算了\(\chi\), 可以利用如下关系:

    设\(d=\gamma_x-\alpha_x\), \(e=\gamma_y-\alpha_y\), \(f=(\gamma_x\gamma_y+\psi)-\chi\), 若满足\(f=de\)当且仅当\(P_0\)正确计算了\(\chi\). 这是因为

    \[\begin{aligned} de&=(\gamma_x-\alpha_x)(\gamma_y-\alpha_y)=\gamma_x\gamma_y-\gamma_x\alpha_y-\gamma_y\alpha_x+\Gamma_{xy}\\ &=(\gamma_x\gamma_y+\psi)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi)\\ &=(\gamma_x\gamma_y+\psi)-\chi=f \end{aligned} \]

    如此, \(\chi\)的正确性规约到验证\((d,e,f)\)是否是一个Beaver triple. 这种方案还可以解决问题1, 因为当\(P_0\)是腐化方时, 实际上生成的是\(\Gamma_{xy}+\Delta\)的份额, 如此\(de=f+\Delta\neq f\).

    BLAZE中的乘法协议的预处理阶段使用了[1]中提出的\(\langle\cdot\rangle\)共享的恶意安全乘法协议\(\Pi_\mathsf{mulZK}\), 具体过程协议如下:

    image-20220320143006197

    给定\([\![x]\!],[\![y]\!]\), 服务器按如下方法本地计算\(\langle d\rangle,\langle e\rangle\): 在执行协议\(\Pi_\mathsf{mulZK}(\mathcal P,d,e)\)时, \(P_0\)得到\(([\lambda_f]_1,[\lambda_f]_2)\), \(P_1\)得到\(([\lambda_f]_1,f+\lambda_f)\), \(P_2\)得到\(([\lambda_f]_2,f+\lambda_f)\). 然后服务器将\([\chi]\)映射为\([\lambda_f]\), 将\(\gamma_x\gamma_y+\chi\)映射为\(f+\lambda_f\), 并按如下提取所需值为:

    \[[\chi]_1=[\lambda_f]_1 ,\quad [\chi]_2=[\lambda_f]_2\qquad\rightarrow\qquad \chi=[\lambda_f]_1+[\lambda_f]_2 \] \[\gamma_x\gamma_y+\psi=f+\lambda_f\qquad \rightarrow \qquad \psi=f+\lambda_f-\gamma_x\gamma_y \] \[[\gamma_{xy}]_j=\gamma_x[\alpha_y]_j+\gamma_y[\alpha_x]_j+[\psi]_j-[\chi]_j,\quad j\in\{1,2\}. \]

    其中, \([\psi]\)由\(P_1,P_2\)通过共同选取随机数\(r\in\mathbb{Z}_{2^\ell}\), 并设定\([\psi]_1=r, [\psi]_2=\psi-r\), 不需要交互即可生成. 则\(P_1,P_2\)有\([\Gamma_{xy}]=[\alpha_x\alpha_y]\). 这因为

    \[\begin{aligned} \Gamma_{xy}&=\gamma_x\alpha_y+\gamma_y\alpha_x+\psi-\chi\\ &=(d+\lambda_d)\lambda_e+(e+\lambda_e)\lambda_d+(f+\lambda_f-\gamma_x\gamma_y)-\lambda_f\\ &=(d+\lambda_d)(e+\lambda_e)-de+\lambda_d\lambda_e+(f-\lambda_x\lambda_y)\\ &=\gamma_x\gamma_y-f+\lambda_d\lambda_e+(f-\gamma_x\gamma_y)=\lambda_d\lambda_e=\alpha_x\alpha_y. \end{aligned} \]

    由于只规约到单个乘法三元组的验证问题, 因此与ASTRA相比, BLAZE将预处理阶段的通信开销从ASTRA的21个环元素降低到3个环元素, 进一步提升了性能. 秘密乘法协议过程如下:

    Mult

    比特抽取协议

    比特抽取协议\(\Pi_\mathsf{bitext}(\mathcal P,[\![v]\!])\): 给定算术份额\([\![v]\!]\), 允许\(\mathcal P\)中的参与方计算\(v\)的最高有效位(符号位)的布尔共享份额\([\![\cdot]\!]^\mathbf B\). 本文中通过混淆电路来构造常数轮的比特抽取协议.

    设\(GC=(u_1,u_2,u_3,u_4,u_5)\)代表输入为\(u_1,u_2,u_3\in\mathbb Z_{2^\ell},u_4,u_5\in\{0,1\}\), 输出为\(y=\mathsf{msb}(u_1-u_2-u_3)\oplus u_4\oplus u_5\)的混淆电路. 令\(u_1=\beta_v,u_2=[\alpha_v]_1,u_3=[\alpha_v]_2\), 使得\(u_1-u_2-u_3=v\). 令\(u_4=r_1,u_5=r_2\), 其中\(r_1\)代表\(P_0\)和\(P_1\)共同选取的随机比特, \(r_2\)代表\(P_0\)和\(P_2\)共同选取的随机比特. 具体协议过程如下:

    image-20220320145143810

    比特转换协议

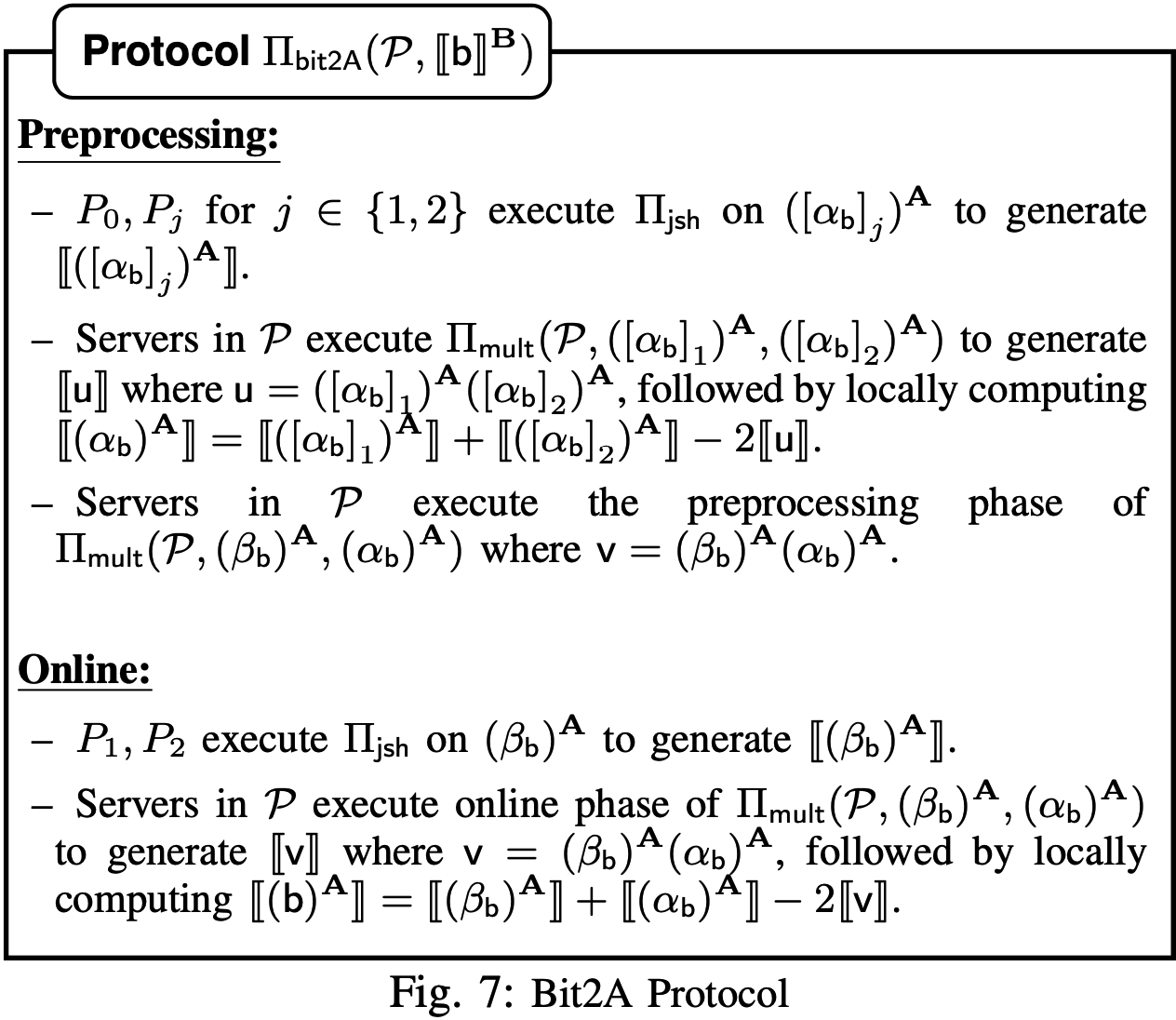
    比特转换协议Bit2A\(\Pi_\mathsf{bit2A}(\mathcal P,[\![b]\!]^\mathbf B)\): 给定单个比特\(b\)的布尔份额\([\![\cdot]\!]^\mathbf B\), 允许\(\mathcal P\)中的参与方得到\(b\)的算术共享份额\([\![b]\!]^\mathbf A\). 记比特\(b\)在\(\mathbb Z_{2^\ell}\)上的值为\((b)^\mathbf A\). 设计思想是基于等式

    \[(b)^\mathbf A=(\beta_b\oplus\alpha_b)^\mathbf A=(\beta_b)^\mathbf A+(\alpha_b)^\mathbf A-2(\beta_b)^\mathbf A(\alpha_b)^\mathbf A. \]

    协议的具体过程如下:

    image-20220320155246874

    点积计算协议

    点积计算协议\(\Pi_\mathsf{dotp}(\mathcal P,\{[\![x_i]\!],[\![y_i]\!]\}_{i\in[n]})\): 给定长度为\(n\)的向量份额\([\![\vec{x}]\!]\)和\([\![\vec y]\!]\), 计算\(z=\vec{x}\odot\vec{y}\)的\([\![\cdot]\!]\)份额.

    通常做法是调用\(n\)次乘法协议\(\Pi_\mathsf{mult}\), 第\(i\)次计算\(z_i=x_i\cdot y_i\)的份额, 最后本地累加即可, 如此通信量将与向量长度\(n\)线性相关.

    本文对点积优化的关键在于不再分开重构每个\(\beta_z^*\)来计算\(\beta_z\), \(P_1,P_2\)本地计算\([\beta_z]=[\beta_{z_1}]+\cdots+[\beta_{z_n}]\)并重构\(\beta_z\); 此外, 对每个\(z_i\), \(P_0\)可以把所有的\(\beta_{z_i}^*\)合并为单个\(\beta_z^*\), 从而发送单个\(\beta_z^*\)给\(P_1,P_2\)进行验证. 具体来说, \(P_0\)计算\(\beta_z^*=\sum_{i=1}^n\beta_z^*\)并发送它的Hash值给\(P_1\)和\(P_2\), 然后\(P_1\)和\(P_2\)可以交叉检验它与\(\beta_z-\sum_{i=1}^n(\beta_{x_i}\cdot\beta_{y_i}-\psi_i)\)的Hash值的一致性. 具体协议过程如下:

    image-20220320171631561

    定点截断协议

    当进行秘密乘法后精度将翻倍, 为防止多次乘法后造成溢出需要对每次乘法后的秘密份额进行截断. 设定点数精度为\(d\), 本文中的截断协议设计思路同ABY3, 但主要的不同在于预处理阶段随机截断对\((r,r^d)\)的生成方法不依赖于RCA: \(P_0,P_1\)随机选取\(R_1\in\mathbb Z_{2^\ell}\), \(P_0,P_2\)随机选取\(R_2\in\mathbb Z_{2^\ell}\), 然后\(P_0\)本地计算\(r=R_1+R_2\)并截断得到\(r^d\). 注意到\(r=2^dr^d+r_d\), 其中\(r_d\)表示\(r\)的后\(d\)个比特组成的环元素, 其他位置为零. 然后, \(P_0\)执行\(\Pi_\mathsf{sh}\)生成\([\![r^d]\!]\). 为了验证\(P_0\)分享的份额的正确性, \(P_1,P_2\)计算\(a=(r-2^dr^d-r_d)\)的\([\cdot]\)份额, 给定\(([r],[\![r^d]\!])\), 验证\(a=0\)是否成立. 具体协议过程如下:

    image-20220320191700465

    正确性: 只需说明\(u=v\), 其中\(u=[r]_1-2^d[r^d]_1-[r_d]_1\), \(v=2^d[r^d]_2+[r_d]_2-[r]_2\). 因为

    \[\begin{aligned} r&=2^dr^d+r_d\\ [r]_1+[r]_2&=2^d([r^d]_{1}+[r^d]_2)+([r_d]_1+[r_d]_2)\\ [r]_1-2^d[r^d]_1-[r_d]_1&=2^d[r^d]_2+[r_d]_2-[r]_2\\ u&=v. \end{aligned} \]

    点积截断协议

    点积截断协议\(\Pi_\mathsf{dotpt}(\mathcal P,\{[\![x_i]\!],[\![y_i]\!]\}_{i\in[n]})\): 给定长度为\(n\)的向量份额\([\![\vec{x}]\!]\)和\([\![\vec y]\!]\), 计算\(z=\vec{x}\odot\vec{y}\)截断后\(z^d\)的\([\![\cdot]\!]\)份额.

    预处理阶段同\(\Pi_\mathsf{dotp}\), 参与方执行\(\Pi_\mathsf{trgen}\)生成截断对\((r,r^d)\). 在线阶段, \(P_1,P_2\)本地计算\((z-r)\)的\([\cdot]\)份额, 然后\(P_1,P_2\)本地截断\((z-r)\)得到\((z-r)^d\)并通过\(\Pi_\mathsf{jsh}\)协议生成\([\![\cdot]\!]\)份额. 最后, 参与方本地计算\([\![z]\!]=[\![(z-r)^d]\!]+[\![r^d]\!]\)并进行一致性验证. 这里为了确保计算的正确性, 与上述点积计算协议不同, \(P_0\)计算的部分被改为\((z-r)^*\)而不是\(\beta_z^*\).

    具体协议过程如下:

    BLAZEdotpt

    安全比较协议

    给定\([\![x]\!],[\![y]\!]\), 安全比较协议计算\((x<y)\)的真值, 即需要抽取\(v=x-y\)的符号位. 为此, 首先本地计算\([\![v]\!]=[\![x]\!]-[\![y]\!]\), 然后使用\(\Pi_\mathsf{bitext}([\![v]\!])\)抽取符号位的布尔份额. 如果需要算术份额, 则再调用\(\Pi_\mathsf{bit2A}\)进行比特转换即可.

    激活函数协议

    1. ReLU激活函数计算协议\(\Pi_\mathsf{relu}(\mathcal P, [\![v]\!])\): 即计算\(\mathsf{relu}(v)=\mathsf{max}(0,v)=\bar{b}\cdot v\), 其中\(b=1\)当且仅当\(v<0\), \(\bar{b}\)是\(b\)的补. 首先参与方执行\(\Pi_\mathsf{bitext}([\![v]\!])\), 得到\([\![b]\!]^\mathbf B\), 然后参与方通过设定\(\beta_{\bar b}=1\oplus\beta_b\), 本地计算\([\![\bar b]\!]^\mathbf B\). 接着执行\(\Pi_\mathsf{bit2A}([\![b]\!]^\mathbf B)\)生成\([\![\bar b]\!]\). 最后, 通过\(\Pi_\mathsf{mult}\)计算\([\![\bar bv]\!]\).
    2. Sigmoid激活函数计算协议\(\Pi_\mathsf{sig}(\mathcal P,[\![v]\!])\): 同SecureML分段函数近似法, 将Sigmoid函数表示为\(\mathsf{sig}(v)=\bar{b}_1b_2(v+1/2)+\bar{b}_2\), 其中, 当\(v+1/2<0\)时, \(b_1=1\); 当\(v-1/2<0\)时, \(b_2=1\). 具体协议过程与\(\Pi_\mathsf{relu}\)协议类似.

    实验

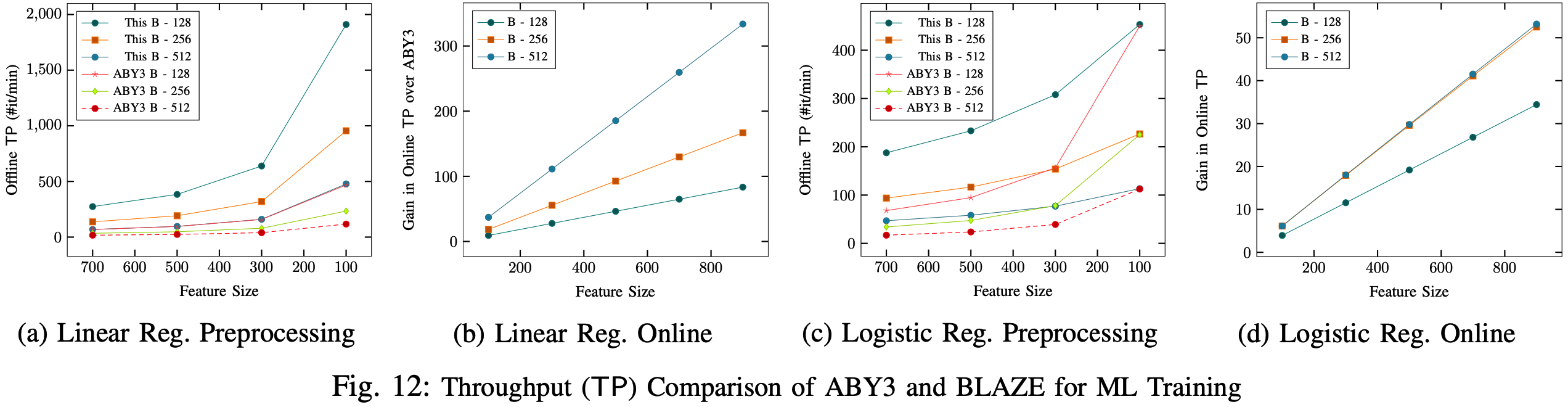
    本文主要以预处理阶段和在线阶段的吞吐量(throughput)为不同方案的对比基准. 下面仅提供部分实验截图.

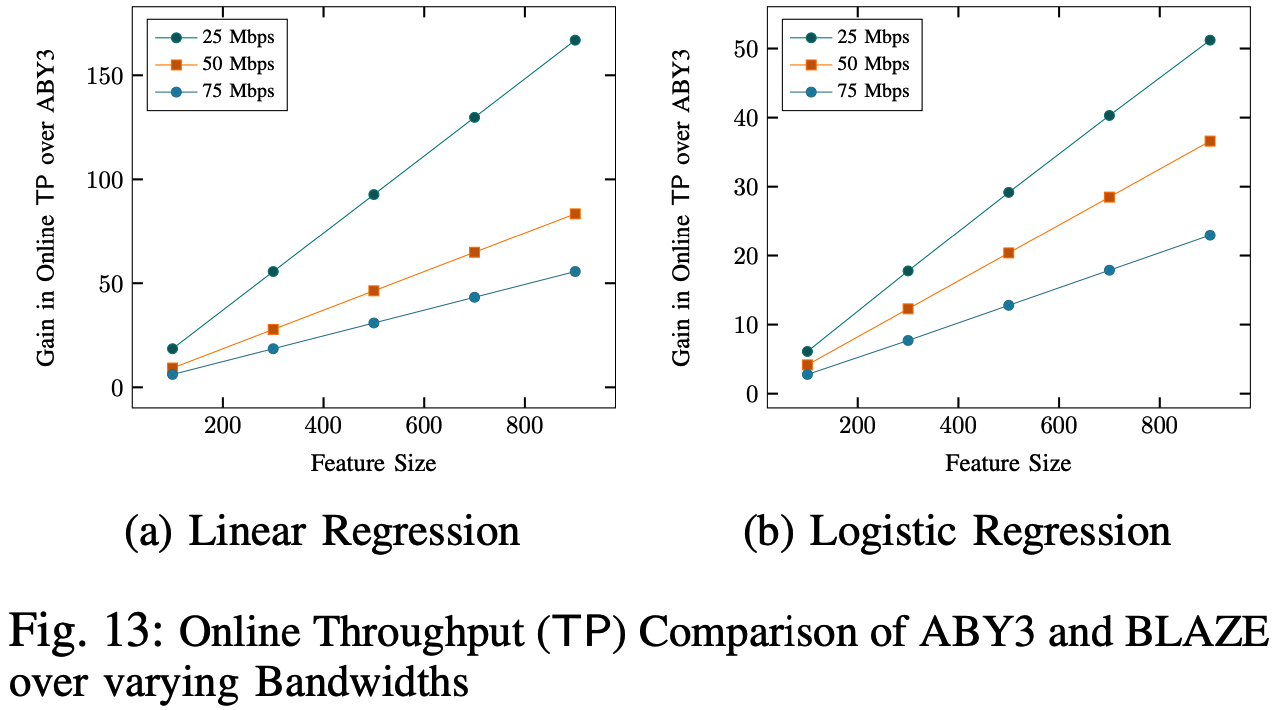
    不同带宽下的ABY3与BLAZE点积协议吞吐量对比:

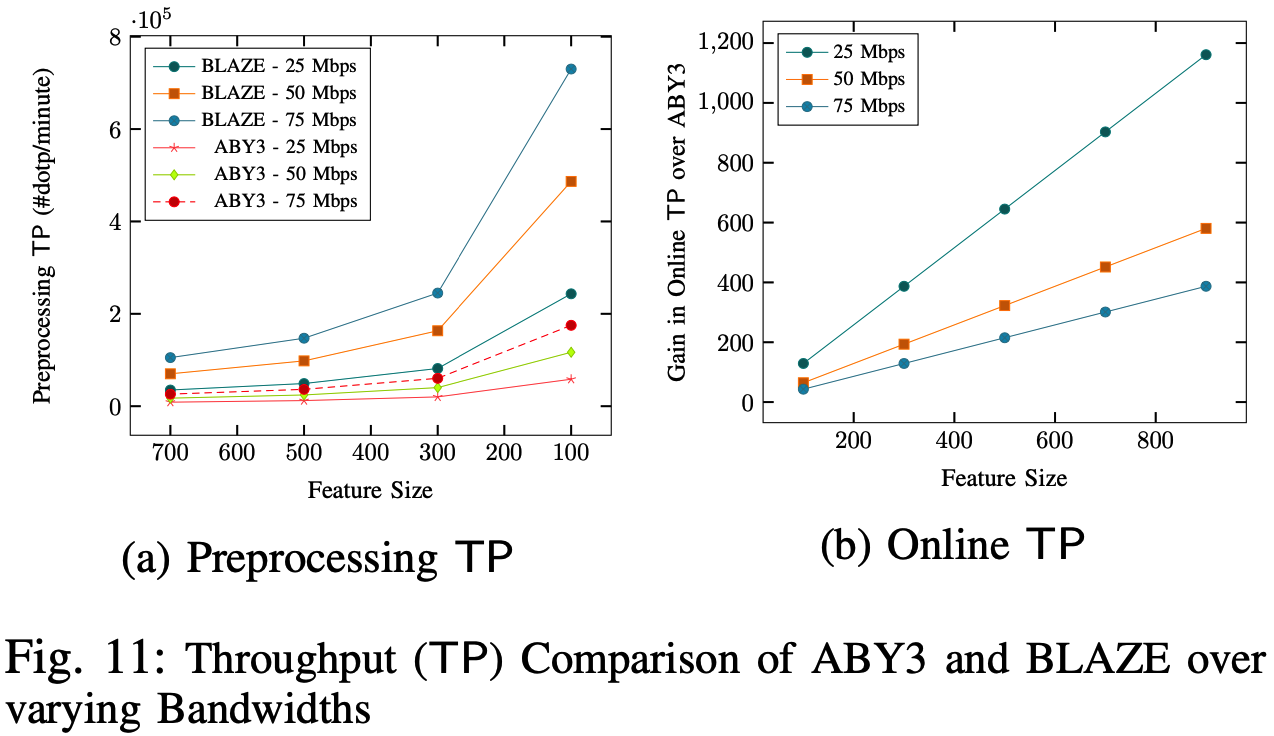
    image-20220320213734911

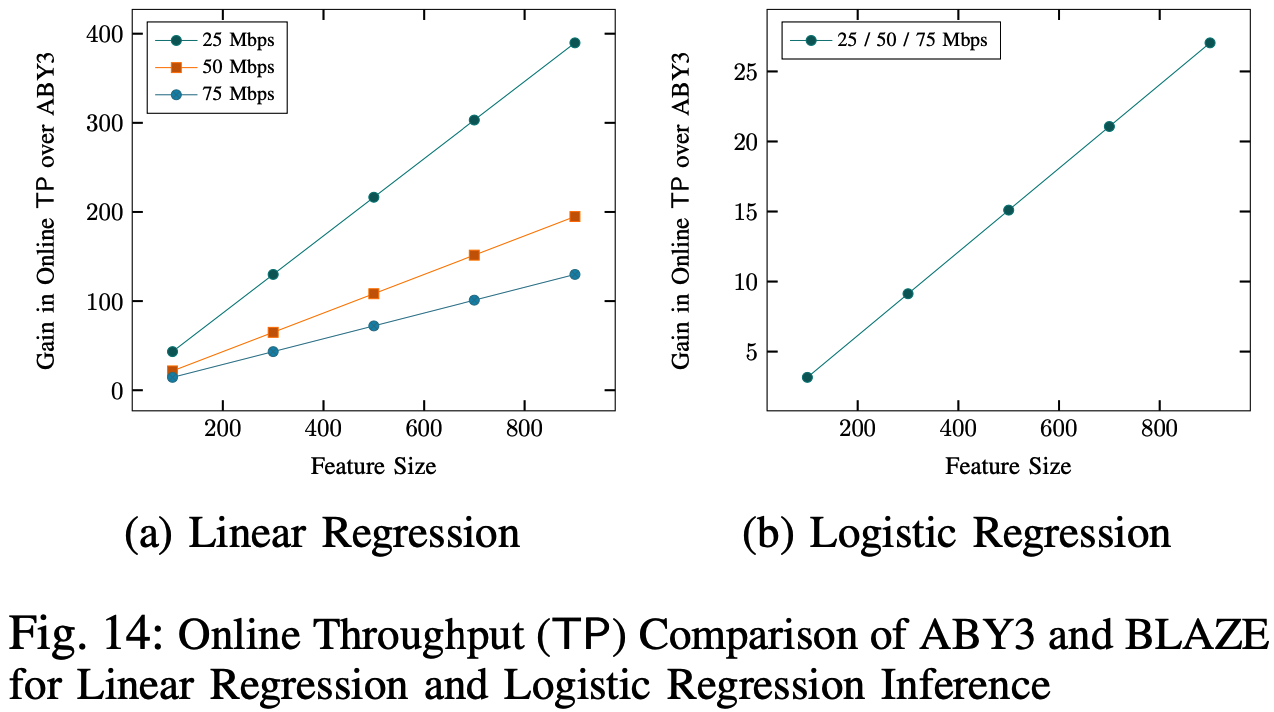
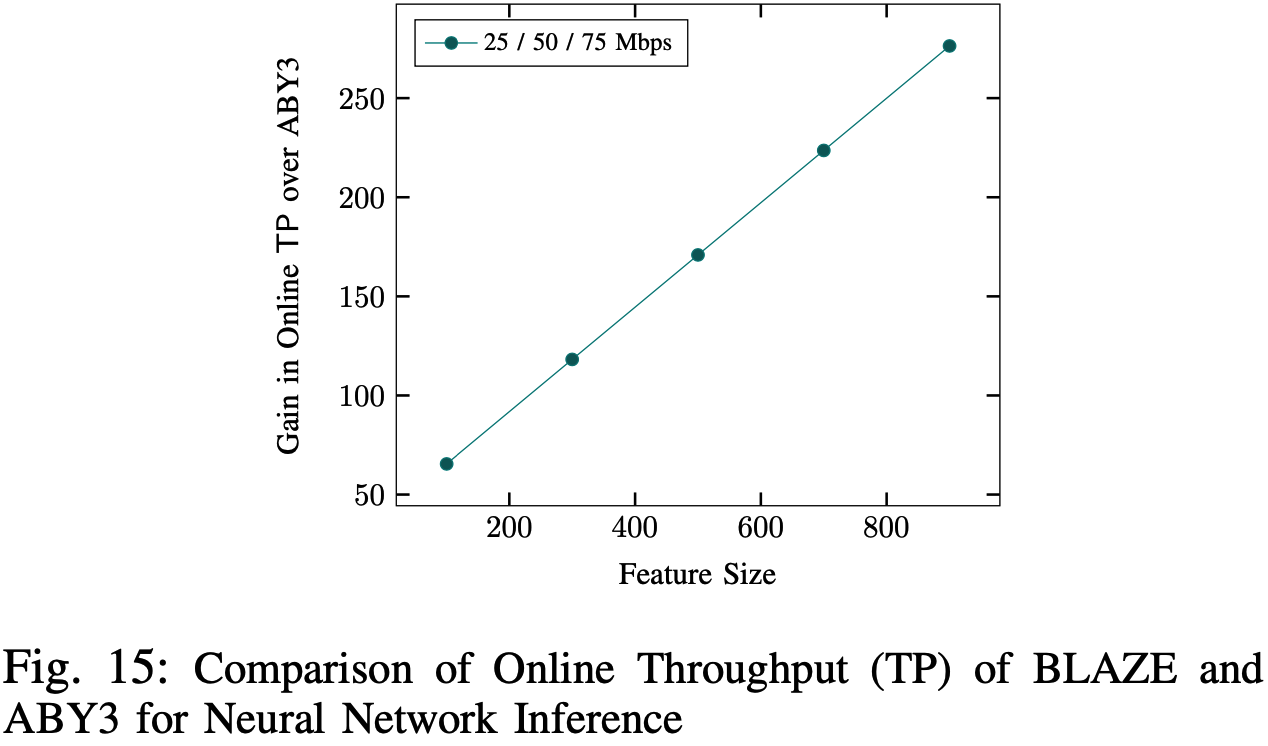
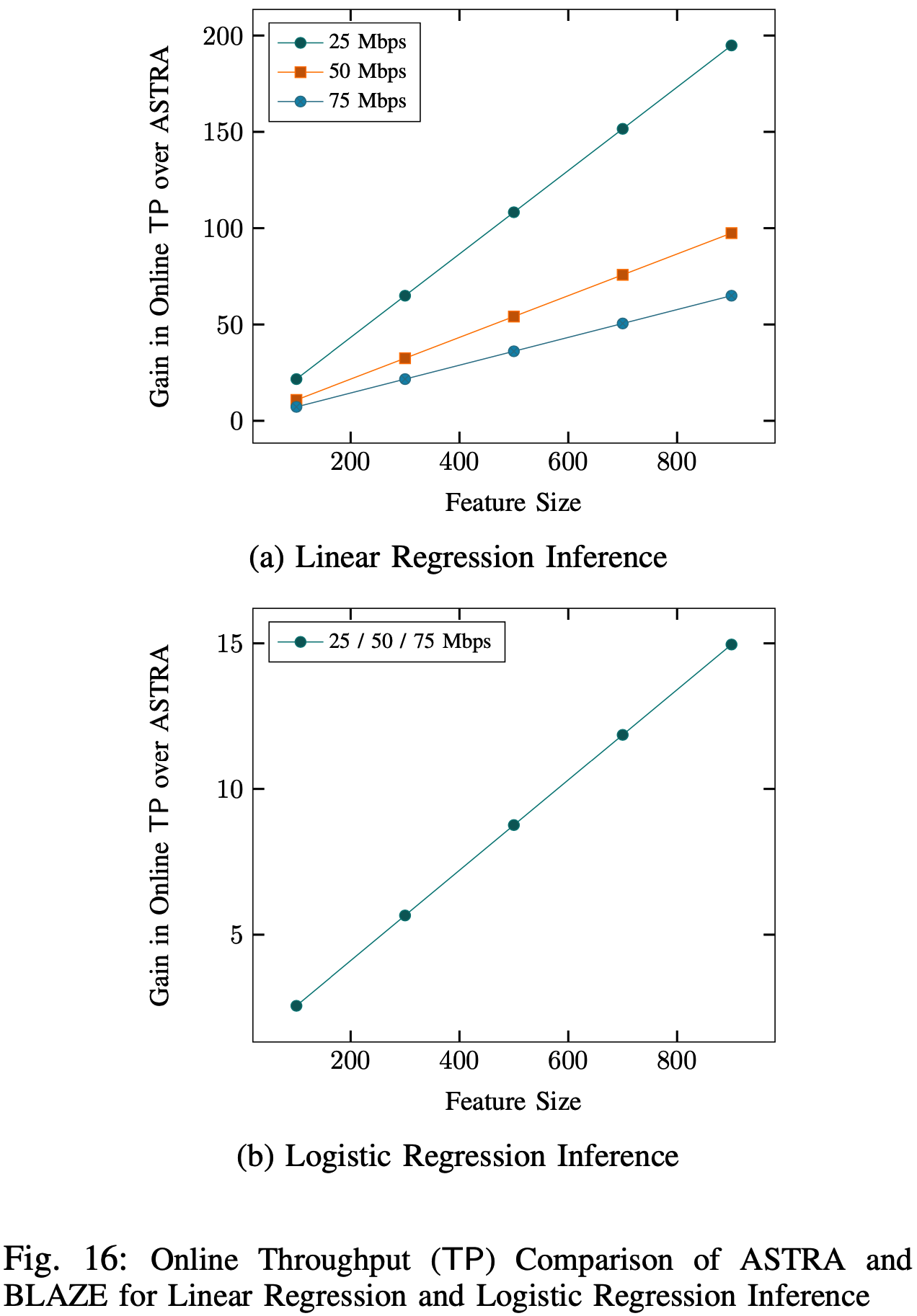
    线性回归与逻辑回归推理部分的吞吐量对比:

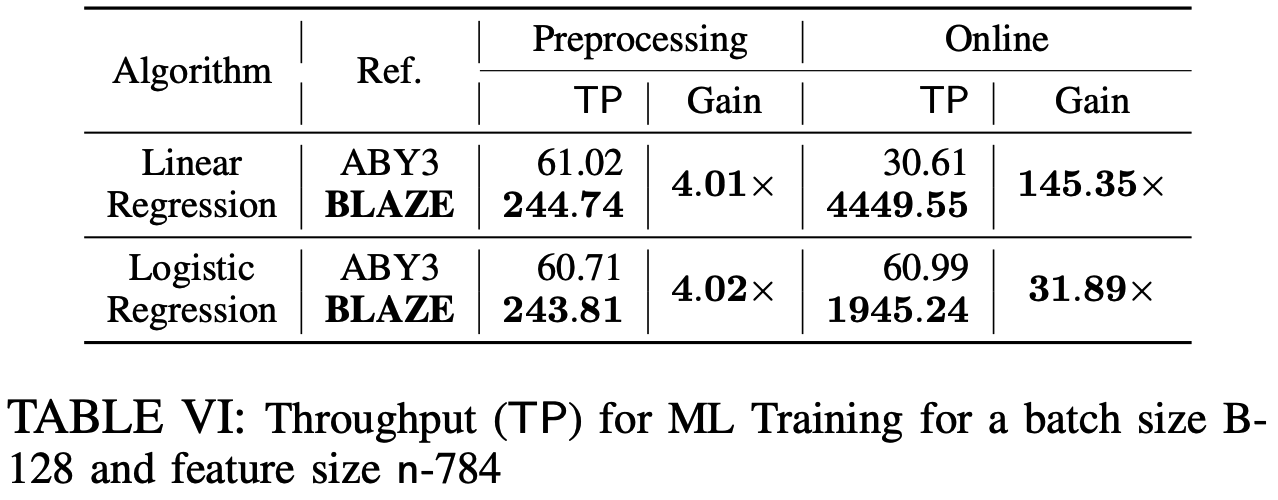
    image-20220320213954206 image-20220320214039017 image-20220320214414667 image-20220320214456070 image-20220320222840218

    与ASTRA对比:

    image-20220320222929474

    总结

    BLAZE框架是环\(\mathbb Z_{2^\ell}\)上至多容忍一个恶意敌手的3PC隐私保护机器学习框架, 是对ASTRA框架的进一步提升, 且与ASTRA一样实现了公平性, 核心思想在于当发现恶意行为时参与方直接中止协议. 与ABY3相比, BLAZE摆脱了对RCA的依赖, 此外, 所设计恶意点积协议在线阶段通信开销与向量长度无关, 但离线阶段仍有关, 有待进一步优化. 与ASTRA相比, BLAZE极大降低了预处理阶段乘法协议的通信开销(21个环元素 VS 3个环元素). 实验发现, BLAZE在不同机器学习任务下的吞吐量都远高于ABY3的方案.

    参考文献

    [1] D. Boneh, E. Boyle, H. Corrigan-Gibbs, N. Gilboa, and Y. Ishai, “Zero-knowledge proofs on secret-shared data via fully linear pcps,” in CRYPTO, 2019, pp. 67–97.

    [2] P. Mohassel and P. Rindal, “ABY3: A mixed protocol framework for machine learning,” in ACM CCS, 2018, pp. 35–52.

    [3] H. Chaudhari, A. Choudhury, A. Patra, and A. Suresh, “ASTRA: High-throughput 3PC over Rings with Application to Secure Prediction,” in ACM CCSW, 2019, pp. 81–92.

    [4] P. Mohassel and Y. Zhang, “SecureML: A system for scalable privacy-preserving machine learning,” in IEEE S&P, 2017, pp. 19–38.


    本文标题: BLAZE: Blazing Fast Privacy-preserving Machine Learning
    本文作者: 云中雨雾
    本文链接: https://weiviming.github.io/16477900515975.html
    本站文章采用 知识共享署名4.0 国际许可协议进行许可
    除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
    最后编辑时间: 2022-03-20T23:27:31+08:00