云中雨雾

    Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference

    2022/02/28 14:09 下午 标签: #隐私保护机器学习

    今天给大家带来的是来自于USENIX Security'22的一篇文章Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference, 作者是来自阿里安全双子座实验室的洪澄博士团队, 文章链接如下: https://eprint.iacr.org/2022/207.

    摘要

    2PC-NN安全推理与实际应用之间仍存在较大性能差距, 因此只适用于小数据集或简单模型. 本文通过仔细设计DNN, 基于格的同态加密、VOLE类型的不经意传输和秘密共享, 提出了一个2PC-NN推理系统Cheetah, 比CCS'20的CrypTFlow2技术开销小的多, 计算效率更快, 通信效率更高. 主要贡献有两点:

    • 基于格的同态加密的协议可在不进行任何昂贵同态rotation操作的情况下评估线性层;
    • 提出了非线性函数的几个精简且通信高效的原语.

    本文的方案在ResNet50神经网络下在WAN进行端到端安全推理需要不到2.5分钟和2.3G通信量, 分别优于CrypTFlow2约5.6倍和12.9倍.

    具体代码已在Github开源: https://github.com/Alibaba-Gemini-Lab/OpenCheetah.

    技术概览

    现有的大多基于HE的方案构造2PC-NN协议存在两大痛点: 一是为使用同态SIMD均摊同态运算操作, 只能在\(\mathbb Z_p\)上工作, 需要额外借助CRT才能支持\(\mathbb Z_{2^\ell}\), 造成额外的同态计算开销, 降低了效率; 二是NN推理的计算中的卷积和矩阵计算涉及大量的同态rotation操作, 是主要的性能瓶颈. Cheetah提出的方案不需要使用SIMD和rotation, 从而避免了这两个问题.

    2PC-NN的非线性计算, 如比较、截断等一直是影响安全推理速度的一大原因. 例如CrypTFlow2中的截断协议通信开销超过50%. VOLE类型OT协议的出现可以更新现有OT扩展, 用于非线性函数的两方安全评估, 但直接应用VOLE类型OT协议并不能达到最佳性能. 本文中优化了以下两点:

    • CrypTFlow2中的截断协议被设计为消除两个概率误差: 溢出误差\(e_0\)和尾部误差\(e_1\), 其中\(\mathrm{Pr}(|e_0|=1)=0.5, \mathrm{Pr}(0<|e_1|<2^{\ell})<\varepsilon\). 其中\(e_0\)对安全推理的结果影响极大, 但\(e_1\)造成的影响几乎可以忽略. 基于此, 可以在不考虑\(e_1\)的情况下, 设计更高效的截断协议来消除\(e_0\).
    • 通过使用VOLE类型OT协议, 在已知最高有效位的前提下, Cheetah实现了更高效的截断协议.

    Cheetah与最先进的2PC协议复杂度比较如表1.

    image-20220224205920181

    预备知识

    威胁模型

    Cheetah是半诚实两方计算设定下构造的. 两方分别为Alice(作为Server)和Bob(作为Client). 在安全推理中, Alice持有DNN, Bob持有神经网络的输入, 如图像. 协议允许Bob获得神经网络架构信息和推理输出, 而Alice根据应用场景的不同要么没有输出, 要么得到安全推理结果.

    符号约定

    \([[n]]\)表示集合\(\{0,1,\cdots,n-1\}\). 多项式表示为\(\hat{a}\), 其第\(j\)个系数表示为\(\hat{a}[j]\). 多维张量表示为\(\mathbf T\).

    多项式算术(Polynomial Arithmetic): 设\(N\)是二次幂数, \(q>0\), 给定整系数多项式\(\hat{a},\hat{b}\in\mathbb A_{N,q}=\mathbb Z_{q}[X]/(X^N+1)\), 在\(\mathbb A_{N,q}\)上的乘积\(\hat{d}=\hat{a}\cdot\hat{b}\)定义如下:

    \[\hat{d}[i]=\sum_{0\leq j\leq i}\hat{a}[j]\hat{b}[i-j]-\sum_{i<j<N}\hat{a}[j]\hat{b}[N+j-i]\bmod q.\tag{1} \]

    这基于事实\(X^N\equiv -1\bmod X^N+1\).

    基于格的同态加密

    Cheetah使用了两种基于格的方案, 即基于LWE和基于RLWE的同态加密方案. 两种方案共享参数: \(\mathsf{HE.pp}=\{N,\sigma,q,p\}\): \(q,p\in\mathbb Z, q\gg p>0\), 明文模数\(p\)可不为素数. 以往的方案中通常设定\(p\)为满足\(p\equiv1\bmod2N\)的素数以使用SIMD技术均摊同态乘法的开销, 但是Cheetah不需要使用SIMD，因而不需要\(p\)是素数.

    RLWE同态加密方案的私钥为\(\mathsf{sk}=\hat{s}\in\mathbb A_{N,q}\), 与之关联的公钥为\(\mathsf{pk}=(\hat{u}\cdot\hat{s}+\hat{e}_0,\hat{u}_0)\), 其中\(\hat{u}_0\in\mathbb A_{N,q}\)是均匀随机的, \(\hat{e}_0\in\mathbb A_{N,q}\)的系数采样自\(\chi_\sigma\)服从标准差为\(\sigma\)的离散高斯分布. 设明文为多项式\(\hat{m}\in\mathbb A_{N,q}\), 则

    • 加密: \((\hat{b},\hat{a})=\mathsf{RLWE}_\mathsf{pk}^{N,q,p}(\hat{m})=(\lfloor\frac{q}{p}\hat{m}\rceil+\hat{e},0)-\hat{u}\cdot\mathsf{pk}\in\mathbb A_{N,p}^2\), 其中\(\hat{e}\in\mathbb A_{N,q}\)的系数采样自\(\chi_\sigma\), \(\hat{u}\in\mathbb A_{N,q}\)的系数均匀随机选取自\(\{0,\pm1\}\);
    • 解密: \(\mathsf{RLWE}_\mathsf{sk}^{-1}(\hat{b},\hat{a})=\lfloor\frac{p}{q}(\hat{b}+\hat{a}\cdot\hat{s})\rceil\equiv\hat{m}\bmod p\).

    LWE同态加密方案的密钥为向量\(\mathbf s\in\mathbb{Z}_q^N\), 设明文为\(m\in\mathbb Z_{p}\), 则

    • 加密: \((b,\mathbf a)=\mathsf{LWE}_\mathbf s^{N,q,p}(m)\in\mathbb Z_{p}^{N+1}\);
    • 解密: \(\mathsf{LWE}_\mathbf{s}^{-1}(b,\mathbf a)=\lfloor\frac{p}{q}(b+\mathbf a^\top\mathbf s)\rceil\equiv m\bmod p\).

    为统一记号, 对所有\(j\in[[N]]\), 令LWE的密钥为\(\mathbf s[j]=\hat{s}[j]\)以统一LWE和RLWE密文. 下文中记LWE的加密为\(\mathsf{LWE}_\mathsf{sk}^{n,q,p}(\hat{m})\).

    RLWE方案支持同态加减法、常量积运算以及抽取(extract). 抽取是指, 给定RLWE密文\((\hat{b},\hat{a})=\mathsf{RLWE}_\mathsf{pk}^{N,q,p}(\hat{m})\), 可以抽取\(\hat{m}\)的第\(k\)个系数为LWE密钥\(\mathsf{sk}\)下\(\hat{m}[k]\)的合法密文\((b,\mathbf a)=\mathsf{Extract}((\hat{b},\hat{a}),k)\).

    扩展: SIMD的Packing操作

    SIMD指的是把一系列数通过中国剩余定理(CRT)打包(pack)到多项式中, 使一次多项式乘法计算可以完成多次明文乘法. 它的计算域必须为素数域\(\mathbb Z_p\). 下面举例说明SIMD中的Packing操作.

    • 如何将需要计算的数据编码为多项式?

      • \(x^n+1\)可以表示为\(n\)个多项式的积: \(x^n+1=(x+a_1)(x+a_2)\cdots(x+a_n)\bmod p\)

        • 例: 设\(p=17\), 多项式阶数\(n=2\), 则\(x^2+1=x^2-17x+52\bmod17=(x-4)(x-13)\bmod 17\).

      • \(f(x)\bmod(x^n+1)\)可以表示为\(n\)个整数: \(x_i=f(x)\bmod(x+a_i)\), 即\(f(x)\bmod(x^n+1)\)“pack”了\(x_i\).

        • 例: \(x\bmod(x^2+1)\)可以表示为\(x\bmod(x-4)\)和\(x\bmod(x-13)\), 即\(x\bmod(x^2+1)\)“pack”了\(4\)和\(13\).
    • 给定\(n\)个整数, 可以通过CRT找到对应的\(f(x)\)来编码它们
      • 例: \(2x-7\)“pack”了\(1\)和\(2\), 因为\(2x-7\bmod(x-4)=1, 2x-7\bmod(x-13)=2\).
    • Packing在模\(p\)上依然保持同态性:
      • 加法: \(x+(2x-7)\)“pack”了\(5\)和\(15\), 因为\(3x-7\bmod(x-4)=5\), \(3x-7\bmod(x-13)=15\bmod17\).
      • 乘法: \(x\cdot(2x-7)\)“pack”了\(4\)和\(9\), 因为\(2x^2-7x\bmod(x^2+1)=-7x-2\), \(-7x-2\bmod(x-4)=4\), \(-7x-2\bmod(x-13)=9\bmod 17\).
    • SIMD: 一次多项式运算完成了\(n\)次整数运算.

    Cheetah中没有使用SIMD, 因此不需要\(p\)为素数. (感谢洪澄老师对SIMD扩展部分的补充)

    不经意传输

    Cheetah的协议非线性计算依赖于Boyle等人于CCS'19提出的VOLE类型OT协议——Silent OT extension1, 它通过低通信量、与输入无关的设定以及纯本地计算两个阶段生成大量Random OT correlation, 而Ferret2和Silver3是Silent OT extension的两个更高效的变种.

    线性层的2PC协议

    全联接层(FC)、卷积层(CONV)、批标准化层(BN)都可以写成一系列内积的形式. Cheetah的线性协议不需要使用SIMD和同态rotation, 其关键在于观察到对多项式乘法公式(1), 若适当地排列多项式系数, 则可以将其视为一系列内积运算. 为此, Cheetah中针对不同层的功能\(\mathcal F\), 通过构造一对自然映射\((\pi_\mathcal F^i,\pi_\mathcal F^w)\)分别用于排列\(\mathcal F\)的输入和权重的多项式系数, 对于任意\(p>1\), 这两个映射是良定义的(well-defined), 这使协议直接接受来自二次幂环\(\mathbb Z_{2^\ell}\)的秘密份额输入. 相比之下, 以往的工作仅支持接受来自有限域\(\mathbb Z_p\)的秘密份额输入, 为支持接受来自二次幂环\(\mathbb Z_{2^\ell}\)的秘密份额输入, 需要借助中国剩余定理将明文模数扩展到大约\((2\ell+1+40)\)比特来实现40比特的统计安全性, 导致计算量和通信量增加\(O((2\ell+1+40)/\ell)\)的倍数.

    全联接层(FC层)

    FC层输入为向量\(\mathbf v\in\mathbb F^{n_i}\), 参数为权重矩阵\(\mathbf W\in\mathbb F^{n_o\times n_i}\)和偏置向量\(\mathbf b\in\mathbb F^{n_0}\), 输出为向量\(\mathbf u=\mathbf{Wv}+\mathbf b\in\mathbb F^{n_o}\), 这里的\(\mathbb F=\mathbb Z_p\). 因此, FC的核心在于计算矩阵向量乘积\(\mathbf u=\mathbf{Wv}\), 这可以分解为向量内积运算, 从而可以使用多项式算术来计算. 直观上看, 两个阶为\(N\)的多项式相乘, 所得结果多项式的\(N-1\)阶的系数是两系数向量反序作内积.

    设\(n_on_i\leq N\), 定义两个映射: \(\pi_\mathrm{fc}^w:\mathbb Z_p^{n_o\times n_i}\mapsto\mathbb A_{N,p}\)和\(\pi_\mathrm{fc}^i: \mathbb Z_p^{n_i}\mapsto\mathbb A_{N,p}\):

    \[\hat{v}=\pi_\mathrm{fc}^i(\mathbf v), \text{其中}~\hat{v}[j]=\mathbf v[j],\\ \hat{w}=\pi_\mathrm{fc}^w(\mathbf W), \text{其中}~\hat{w}[i\cdot n_i+n_i-1-j]=\mathbf W[i,j]. \tag{4} \]

    其中, \(i\in[[n_o]],j\in[[n_i]]\), 且\(\hat{v},\hat{w}\)的所有其他系数均设为0. 则多项式的乘积\(\hat{u}=\hat{w}\cdot\hat{v}\in\mathbb A_{N,p}\)的某些系数直接给出了\(\mathbf{Wv}\equiv\mathbf u\bmod p\).

    性质1: 给定两个多项式\(\hat{v}=\pi_\mathrm{fc}^{i}(\mathbf v),\hat{w}=\pi_\mathrm{fc}^w(\mathbf W)\in\mathbb A_{N,p}\), 通过环\(\mathbb A_{N,p}\)上的乘积\(\hat{u}=\hat{v}\cdot\hat{w}\)可以对\(\mathbf{Wv}\equiv\mathbf u\bmod p\)进行求解, 即对于所有\(i\in[[n_o]]\), \(\mathbf u[i]=\hat{u}[i\cdot n_i+n_i-1]\).

    证明: 对于每个\(i\in[[n_o]]\), 记\(\tilde{n}_i=i\cdot n_i+n_i-1\). 根据公式(1)的定义以及当\(j\geq n_i\)时, \(v[j]=0\), 我们有

    \[\hat{u}[\tilde{n}_i]=\sum_{0\leq j<n_i}\hat{v}[j]\hat{w}[n_i-j]=\sum_{0\leq j<n_i}\mathbf v[j]\mathbf{W}[i,j]=\mathbf{u}[i]. \]

    根据性质1, \(\hat{u}\)的系数除了\(\hat{u}[\tilde{n}_i]\)外, 会泄漏\(\mathbf{Wv}\)的额外信息, 为此, Alice还使用抽取函数\(\mathsf{Extract}(\cdot)\)从\(\hat{u}\)中抽取所需的系数. 文章举例如图3.

    SIMD中把一系列数通过CRT打包(pack)到多项式中, 使一次多项式乘法计算可以完成多次明文乘法, 而Cheetah中则直接把这些数写在多项式系数上, 虽然这样做会导致不能通过一次多项式乘法完成多次明文乘法(多项式相乘后系数会变乱), 但刚好能做卷积, 如图3. (感谢洪澄老师的说明)

    image-20220224202332806

    若\(n_on_i>N\), 则将权重矩阵切分为\(\bar{n}_o\times\bar{n}_i\)子矩阵, 使得\(\bar{n}_o\bar{n}_i\leq N\), 这里\(\bar{n}_o\)和\(\bar{n}_i\)是只要满足约束, 可自由选取的公开参数. 若\(n_i\nmid\bar{n}_i\)或\(n_o\nmid\bar{n}_o\), 则通过Zero padding用0补足, 从而将\(n_o\times n_i\)矩阵乘法转化为更小的\(\bar{n}_o\times\bar{n}_i\)矩阵乘法. 具体协议如图2.

    image-20220224205031777

    复杂度分析: Bob加密并发送了\(n_i'\)个RLWE密文给Alice. Alice计算了\(n_o'n_i'=O(n_on_i/N)\)个同态乘法和加法. Alice发送\(n_o\)个LWE密文给Bob解密. 可通过优化压缩通信量为\(O((n_o+n_o'N)\log_2q)\)比特.

    卷积层(CONV层)

    \(\mathbb F\)上的二维步幅卷积\(\mathsf{Conv2D}(\mathbf T,\mathbf K;s)\)作用在一个步幅为\(s>0\)、核为四维张量\(\mathbf K\in\mathbb F^{M\times C\times h\times h}\)的三维张量\(\mathbf T\in\mathbb F^{C\times H\times W}\)上, 生成三维张量\(\mathbf T'\in\mathbb F^{M\times H'\times W'}\), 其中\(H'=\lfloor(H-h+s)/s\rfloor, W'=\lfloor(W-h+s)/s\rfloor\), \(M\)表示卷积中使用的核数, \(h\)表示核的尺寸. 从数学的观点来看, 二维步幅卷积可以看作对输出张量\(\mathbf T'\)的每个位置\((c',i',j')\)计算权重和:

    \[\mathbf{T}^{\prime}\left[c^{\prime}, i^{\prime}, j^{\prime}\right]=\sum_{c \in[[C]] \atop l, l^{\prime} \in[[h]]} \mathbf{T}\left[c, i^{\prime} s+l, j^{\prime} s+l^{\prime}\right] \mathbf{K}\left[c^{\prime}, c, l, l^{\prime}\right]. \tag{2} \]

    首先考虑最简单的情况\(H=W=h, M=1\), 此时输入张量的形状与卷积核相同, 则公式(2)的计算变为逐行逐通道连接\(\mathbf T\)和\(\mathbf K\)的两个向量的内积. 通常情况下, 可以将二维卷积计算看作一系列\(h^2\)个值的内积运算.

    设\(MCHW\leq N\), 定义映射\(\pi_\mathrm{conv}^i:\mathbb Z_p^{C\times H\times W}\mapsto\mathbb A_{N,p}\)和\(\pi_\mathrm{conv}^w:\mathbb Z_p^{M\times C\times h\times h}\mapsto\mathbb A_{N,p}\):

    \[\hat{t}=\pi_\mathrm{conv}^i(\mathbf T)~\mathrm{使得}~\hat{t}[cHW+iW+j]=\mathbf T[c,i,j] \\ \hat{k}=\pi_\mathrm{conv}^w(\mathbf K)~\mathrm{使得}~\hat{k}[O-c'CHW-cHW-lW-l']=\mathbf K[c',c,l,l'],\tag{5} \]

    其中\(O=HW(MC-1)+W(h-1)+h-1\), 且\(\hat{t}\)和\(\hat{k}\)的所有其他系数设为0. 则多项式的乘积\(\hat{t}\cdot\hat{k}\in\mathbb A_{N,p}\)的某些系数直接给出了二维卷积的结果. 类似于FC, Alice需要使用抽取函数保护可能的泄漏. 具体协议见图4.

    image-20220225093248907

    性质2: 给定两个多项式\(\hat{t}=\pi_\mathrm{conv}^i(\mathbf T), \hat{k}=\pi_\mathrm{conv}^w(\mathbf K)\in\mathbb A_{N,p}\), 卷积公式(2)可以通过环\(\mathbb A_{N,p}\)上的多项式乘积\(\hat{t}'=\hat{t}\cdot\hat{k}\)来求解, 即对\(\mathbf T'\)的所有位置\((c',i',j')\), \(\mathbf T'[c',i',j']=\hat{t}'[O-c'CHW+i'sW+j's]\), 其中\(O=HW(MC-1)+W(h-1)+h-1\).

    现在考虑大张量情况下的一般情形, 主要做法与FC类似, 仍是需要将大的输入张量和核切分为更小的子块使之适合\(\mathbb A_{N,p}\)上的多项式运算, 并对边缘块不足的部分通过Zero padding用零补足.

    首先将切分窗口\((M,C,H,W)\)轴坐标分别定义为可自由选择的\(M_w,C_w,H_w,W_w\), 但需满足约束条件: \(0<M_w\leq M\), \(0<C_w\leq C\), \(h\leq H_w\leq H\), \(h\leq W_w\leq W\), \(M_wC_wH_wW_w\leq N\). 本文中为了最小化Bob发送的密文数量, 选取\(H_w,W_w\)使得乘积\(\lceil\frac{C}{\lfloor N/(H_wW_w)\rfloor}\rceil\cdot\lceil\frac{H-h+1}{H_w-h+1}\rceil\cdot\lceil\frac{W-h+1}{W_w+h-1}\rceil\)最小化, 此时\(C_w=\min(C,\lfloor N/(H_wW_w)\rfloor)\), \(M_w=\min(M,\lfloor N/(C_wH_wW_w)\rfloor)\).

    由于沿\(M\)轴上的卷积独立于每个子核, 因而可以将\(M\)轴切分为\(d_M=\lceil\frac{M}{M_w}\rceil\)个组, 每个组包含\(M_w\)个子核. 类似地, 沿\(C\)轴上的卷积需要额外的加法, 而同态运算支持加法, 因此我们也可以安全无重叠地沿着\(C\)轴进行切分.

    当\(h>1\)时, 需要额外关注\(H\)轴和\(W\)轴的切分, 以确保步幅窗口不会切分到两个邻近的分区中. 本文中分别将\(H\)轴切分为\(d_H=\lceil\frac{H-h+1}{H_w-h+1}\rceil\)块, 将\(W\)轴切分为\(d_W=\lceil\frac{W-h+1}{W_w-h+1}\rceil\)块. 对于子块\(\alpha\in[[d_H]],\beta\in[[d_W]]\), 包含了\(\mathbf T\)从第\(\alpha(H_w-h+1)\)行开始的\(H_w\)的连续行, 从第\(\beta(W_w-h+1)\)列开始的\(W_w\)的连续列. 举例如图5所示, 当\(h>1\)时, 相邻块存在重叠, 虚线部分是Zero padding.

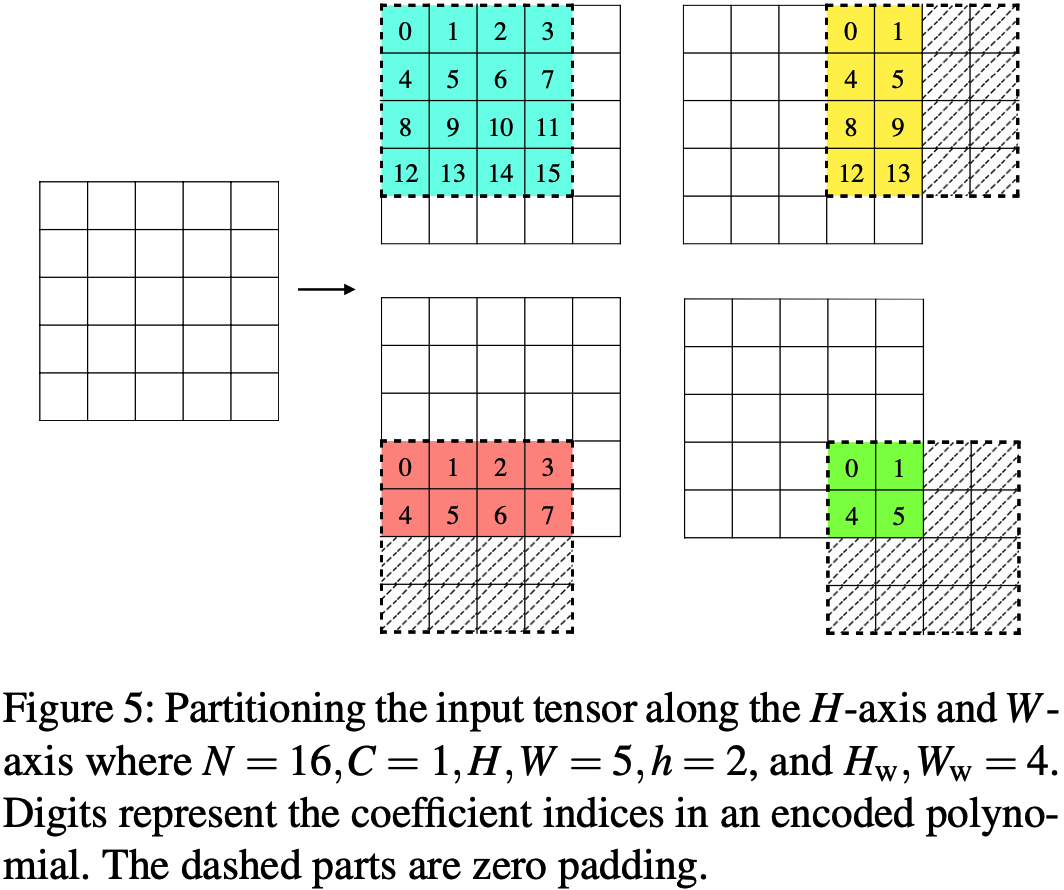
    image-20220225112619578

    整个卷积层的安全协议完整版如下图11.

    image-20220225141352247

    复杂度分析: Bob发送了\(O(CHW/N)\)个RLWE密文给Alice, 大约\(O(2CHW\log_2q)\)比特. Alice计算了\(O(MCHW/N)\)个同态加法和乘法, 并发送\(O(\frac{M}{M_w}H'W')\)个LWE密文给Bob解密. 整个协议的计算复杂度与核大小\(h\)无关.

    批标准化层(BN层)

    在DNN中, BN层\(\mathsf{BN}(\mathbf{T};\alpha,\beta)\)取三维张量\(\mathbf T\in\mathbb F^{C\times H\times W}\)为输入, 参数\(\mu\in\mathbb F^C\)是缩放向量, \(\theta\in\mathbb F^C\)是移位向量, 输出相同形状的三维张量\(\mathbf{T}'\). 对于所有的\(c\in[[C]],i\in[[H]],j\in[[W]]\),

    \[\mathbf T'[c,i,j]=\mu[c]\mathbf T[c,i,j]+\theta[c].\tag{3} \]

    若将\(\mathbf T\)看作大小为\(HW\)的向量, 可以将公式(3)看成标量-向量乘法和向量加法的形式.

    于是我们可以通过映射张量的每个通道到多项式以使用标量多项式乘法计算BN, 这会使安全BN协议通信\(O(C\lceil HW/N\rceil)\)个密文. 为此, 可以通过“堆砌”多通道为单个多项式来降低通信成本.

    设\(C^2HW\leq N\), 定义映射: \(\pi_\mathrm{bn}^i:\mathbb Z_p^{C\times H\times W}\mapsto\mathbb A_{N,p}\)和\(\pi_\mathrm{bn}^w:\mathbb Z_p^{C}\mapsto\mathbb A_{N,p}\):

    \[\hat{t}=\pi_\mathrm{bn}^i(\mathbf T)~\text{使得}~\hat{t}[cCHW+iH+j]=\mathbf T[c,i,j]\\ \hat{a}=\pi_\mathrm{bn}^w(\alpha)~\text{使得}~\hat{a}[cHW]=\alpha[c], \]

    其中\(c\in[[c]]\), \(i\in[[H]]\), \(j\in[[W]]\), \(\hat{t}\)和\(\hat{a}\)的所有其他系数均设为0. 如此, 多项式乘积\(\hat{t}'=\hat{t}\cdot\hat{a}\)的某些系数给出了公式(3)的乘法部分结果, 即对所有\((c,i,j)\)位置, 有

    \[\hat{t}'[cCHW+cHW+iH+j]=\mathbf T[c,i,j]\alpha[c]. \]

    当\(C^2HW>N\), 类似于上面的方法, 将\(\mathbf T\)切分成形状为\(C_w\times H_w\times W_w\)的子块, 使得\(C_w^2H_wW_w\leq N\). 由于每个通道在BN计算中都是独立进行的, 因此可以将两个映射直接应用于\(\mathbf T\)的子块. 整个协议如下图6:

    image-20220225172349412

    复杂度分析: Bob加密并发送\(O(CHW/N)\)个RLWE密文给Alice. Alice进行\(O(CHW/N)\)次同态运算. 最后, Alice发送\(O(CHW)\)个LWE密文给Bob解密.

    非线性函数的2PC优化协议

    CrypTFlow2中对非线性计算协议大量应用了IKNP类型OT扩展协议, Cheetah中则使用VOLE类型OT扩展协议来简化和优化CrypTFlow2的非线性计算协议.

    本文主要使用\(\binom{2}{1}-\mathtt{OT}_\ell\), \(\binom{2}{1}-\mathtt{COT}_\ell\)和\(\binom{n}{1}-\mathtt{OT}_\ell\). 由于使用的是VOLE类型OT扩展协议, 因此其调用\(\binom{2}{1}-\mathtt{ROT}_\lambda\)的均摊通信开销几乎为零. 它与CryptTFlow2的对比如下表2, 当\(n\)和消息长度\(\ell\)很小时, 本文的方案有明显优势, 对所有神经网络安全推理中的协议均如此(通常\(n\leq16,\ell\leq 2\)).

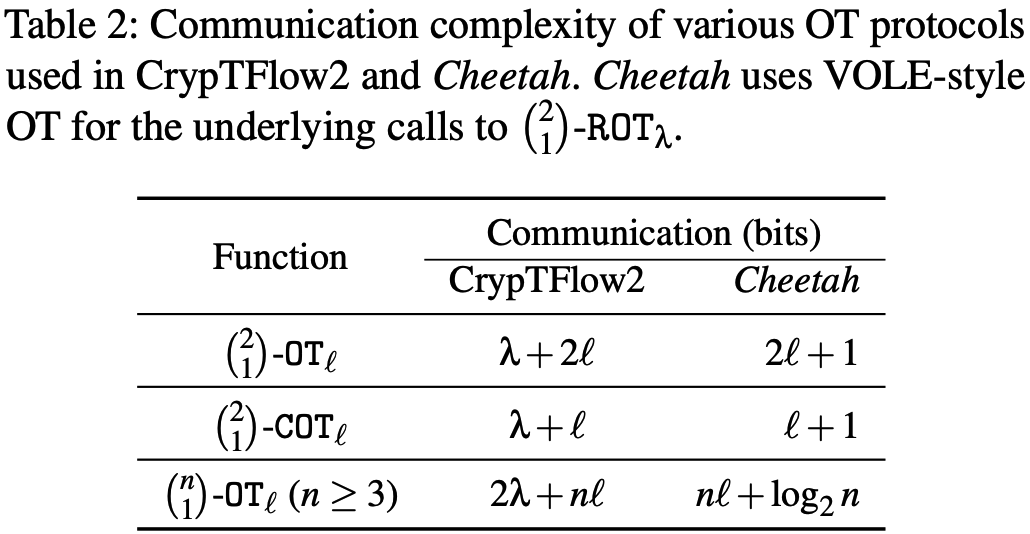
    image-20220225202618987

    百万富翁协议

    百万富翁协议即比较协议, 几乎是所有非线性层的核心组件, 如ReLU、截断和池化. Cheetah中的比较协议与CrypTFlow2的主要不同之处在于底层的\(\mathcal F_\mathrm{AND}\)使用VOLE类型OT扩展协议实现而不是IKNP类型OT扩展协议.

    设\(x,y\in\{0,1\}^\ell\), \(\mathcal F_\mathrm{AND}\)是取\(x\)和\(y\)的布尔份额为输入并输出\(x\wedge y\)的布尔份额的功能函数, 协议如图12.

    image-20220225220955682

    首先回顾CrypTFlow2中的比较协议,

    1. 每方将各自的\(\ell\)比特输入分解为\(m\)比特小块. 设\(x_j\)和\(y_j\)分别代表\(P_0\)和\(P_1\)的第\(j\)小块. 两方调用两次\(\binom{2^m}{1}-\mathtt{OT}_1\)分别计算\(\mathtt{lt}_j=\mathbf 1\{x_j<y_j\}\)和\(\mathtt{eq}_j=\mathbf 1\{x_j=y_j\}\).
    2. 两方使用\(\mathcal F_\mathrm{AND}\)组合前面的输出, 根据\(\mathbf 1\{x<y\}=\mathbf 1\{x_1<y_1\}\oplus(\mathbf 1\{x_1=y_1\}\wedge\mathbf 1\{x_0<y_0\})\)对深度为\(\log(\ell/m)\)的二叉树进行求值, 其中\(x=x_1||x_0,y=y_1||y_0\).

    关于CrypTFlow2中的比较协议更详细的解读可以参考知乎中科院大神@酸菜鱼 的这篇解读文章.

    CrypTFlow2中对步骤2提出了多种优化方案以分析\(\mathcal F_\mathrm{AND}\)在IKNP类型OT扩展协议的效率, 例如使用\(\binom{16}{1}-\mathtt{OT}_2\)生成两个Beaver三元组和\(\binom{8}{1}-\mathtt{OT}_2\)生成关联元组. 然而在Cheetah中, 则使用更高效的\(\binom{2}{1}-\mathtt{ROT}_1\)生成Beaver三元组. 尽管如此, CrypTFlow2在步骤1中分成\(m\)比特块求值的方案极大地减少了直接对逐比特生成的深度为\(\log\ell\)的二叉树进行求值的原始方案所使用AND门数量, 表3对三种方案的通信复杂度进行了比较.

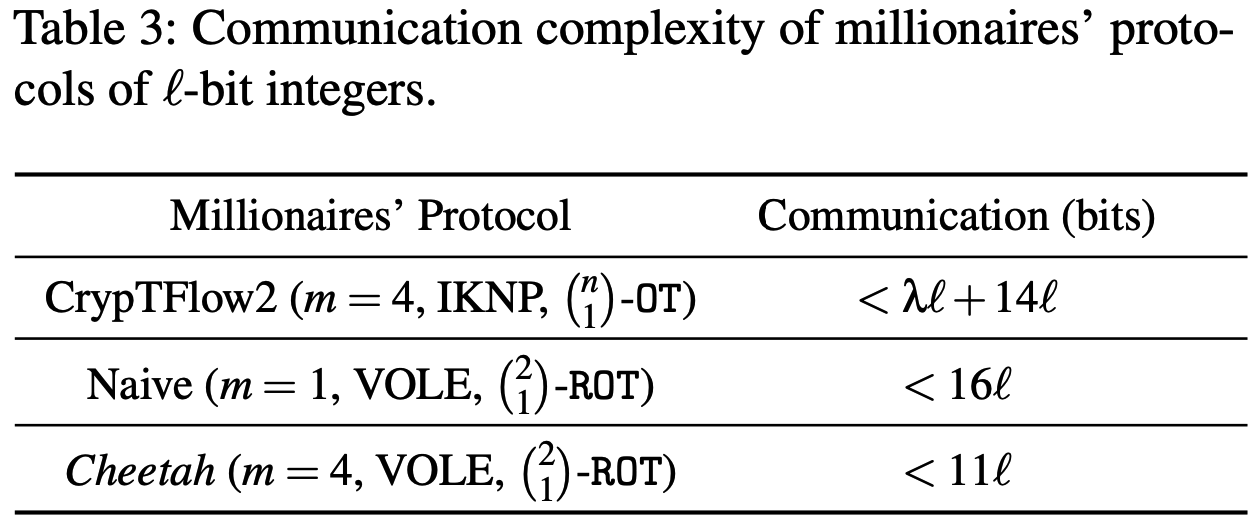
    image-20220227120140958

    下文中, 设\((\langle m\rangle_2^A,\langle m\rangle_2^B)=\mathsf{Mill}^\ell(x,y)\)代表百万富翁协议, 其中Alice输入为\(x\), Bob输入为\(y\), 得到\(\langle m\rangle_2^A\oplus\langle m\rangle_2^B=\mathbf 1\{x>y\}\)的布尔分享份额.

    近似截断

    在定点数计算中, 截断是乘法计算后的必要步骤.

    一比特近似截断

    DELPHI3、ABY3、SecureML中使用的本地截断的误差来源有两个: 一是当秘密份额之和溢出时造成极大的误差; 二是以1/2的概率造成最后一比特误差. CrypTFlow2中以繁重、faithful截断协议来约束这两种情况. 但本文通过实验发现, 在实际应用中, 当\(\ell\leq 64\)时, 前者造成极大误差这个概率是不可忽略的, 而最后一比特造成的误差实际上不会影响机器学习预测模型的质量4. 由于这个原因, 可以移除最后一比特误差的约束来构造更简洁轻量的截断协议, 从而显著降低通信和计算开销.

    性质3: 给定无符号\(\ell\)比特整数\(x\)和它的算术分享份额\(x_0\)和\(x_1\), 定义\(w=\mathbf 1\{x_0+x_1>2^\ell-1\}\). 设\(c\)是一比特整数0或1, 有\((x_0\gg f)+(x_1\gg f)-w\cdot 2^\ell=(x\gg f)-c\).

    性质3中的\(w\)取值与\(x_0+x_1>_?2^\ell-1\)相关, 是导致本地截断出现大误差的原因. 设\(\mathcal F_\mathrm{B2A}^{2^f}\)表示将\(x\in\{0,1\}\)的布尔共享份额转化为在\(\mathbb Z_{2^f}\)上的\(x\)的算术共享份额, 可通过VOLE类型OT协议实例化的\(\binom{2}{1}-\mathtt{COT}_f\)来构造具体协议(与CrypTFlow2的B2A协议相同, 只是OT类型不同, 如下图13). 如此可构造一比特近似截断协议如下图8.

    Cheetah138

    已知符号位的近似截断

    当输入的符号位/最高位(MSB)已知时, 可以构造更高效的2PC截断协议. 设已知输入为正, 即其最高位为0, 则\(w\)的计算可以只调用一次\(\binom{2}{1}-\mathtt{OT}_1\)完成, 而不需要借助百万富翁协议, 此时\(w=\mathtt{msb}(\langle x\rangle^A)\vee\mathtt{msb}(\langle x\rangle^B)\), 如此可构造图9的协议. 类似地, 当最高位为1时, \(w=\mathtt{msb}(\langle x\rangle^A)\wedge\mathtt{msb}(\langle x\rangle^B)\).

    image-20220227202321566

    通信复杂度分析: 比起CrypTFlow2, Cheetah通信开销更小, 如下表所示.

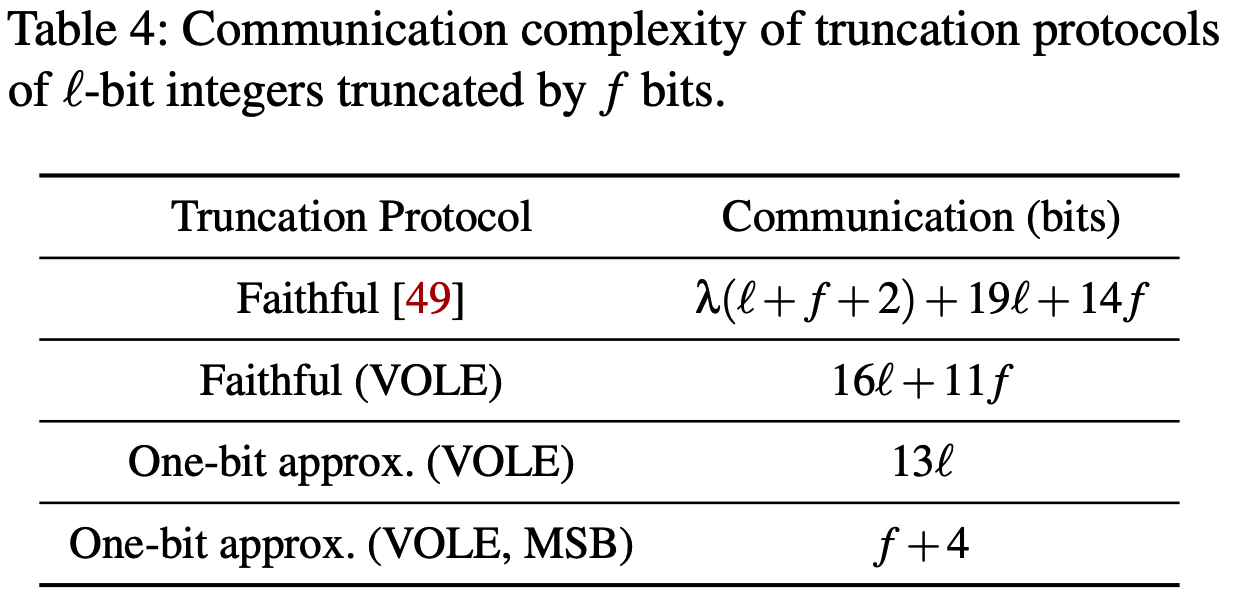
    image-20220227203333646

    优化

    计算优化

    通常BN层放在CONV层或FC层后面. BN融合技术可以将BN操作并入CONV层中, 成为新CONV层, 相比先CONV后BN, 可大大减少计算量. 由于Alice已知BN层和CONV层的权重, 因此可以通过BN融合(fusion)技术来减少\(\mathsf{HomBN}\)的计算. 此外, 通过使用BN融合技术, 还可以节省一个深度的定点数乘法从而减少截断的计算.

    通信优化

    文章还给出了减少Alice通信开销的两个优化方法, 主要是减少Alice发送的HE密文数量.

    1. 若某些LWE密文抽取自相同的RLWE密文, 则这些LWE密文具有相同的向量\(\mathbf a\), 因而Alice可以只发送一次该向量.
    2. 来自于对LWE解密算法的观察. 假设Alice需要发送LWE密文\((b,\mathbf a)\in\mathbb Z_q^{N+1}\)给Bob解密, 则Alice只需发送\(b\)和\(\mathbf a\)中元素的某些高位比特给Bob, 并忽略剩下低位到最后的部分, 因为这部分对解密来说是无用的. 具体来说, Alice可以忽略\(b\)的后\(\ell_b=\lfloor\log_2(q/p)\rfloor-1\)比特和\(\mathbf a\)中元素的后\(\ell_a=\lfloor\log_2(q/6.6\sqrt{N}p)\rfloor\)比特. 可以证明Bob对这样的密文解密失败的几率可忽略不计. 如此Alice可以节省16%~25%的通信开销.

    实验

    本文的协议可以使用任意VOLE类型的OT扩展协议实现, 本文代码使用的是Ferret的方案2. 涉及的开源库有: SEAL, HEXL acceleration, EMP-toolkit. 具体代码已在Github开源: https://github.com/Alibaba-Gemini-Lab/OpenCheetah.

    实验环境: 阿里云ecs.c7.2xlarge, 2.70GHz处理器, 16GB RAM.

    实验部分主要与CrypTFlow2的\(SCI_\mathsf{HE}\)开源库进行对比. 实验数据中的通信量是指Alice和Bob的所有信息发送量, 时间是指不同网络设置(LAN/WAN)下的端到端时间, 但两者都不包括一次性设定(如密钥生成和Base-OT)的通信量和时间.

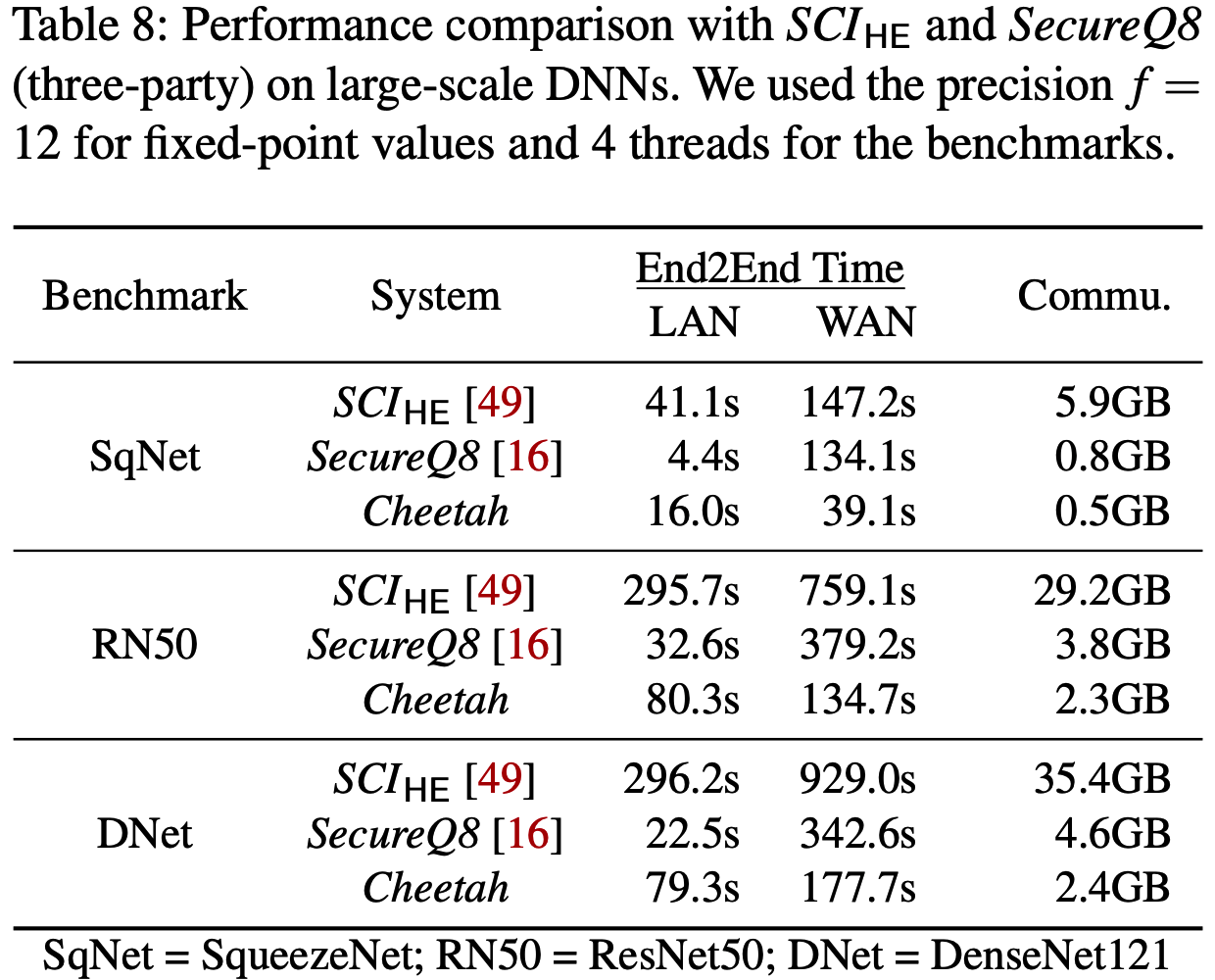
    线性协议对比: 计算快约1.3~20倍, 通信开销低1.5~2倍.

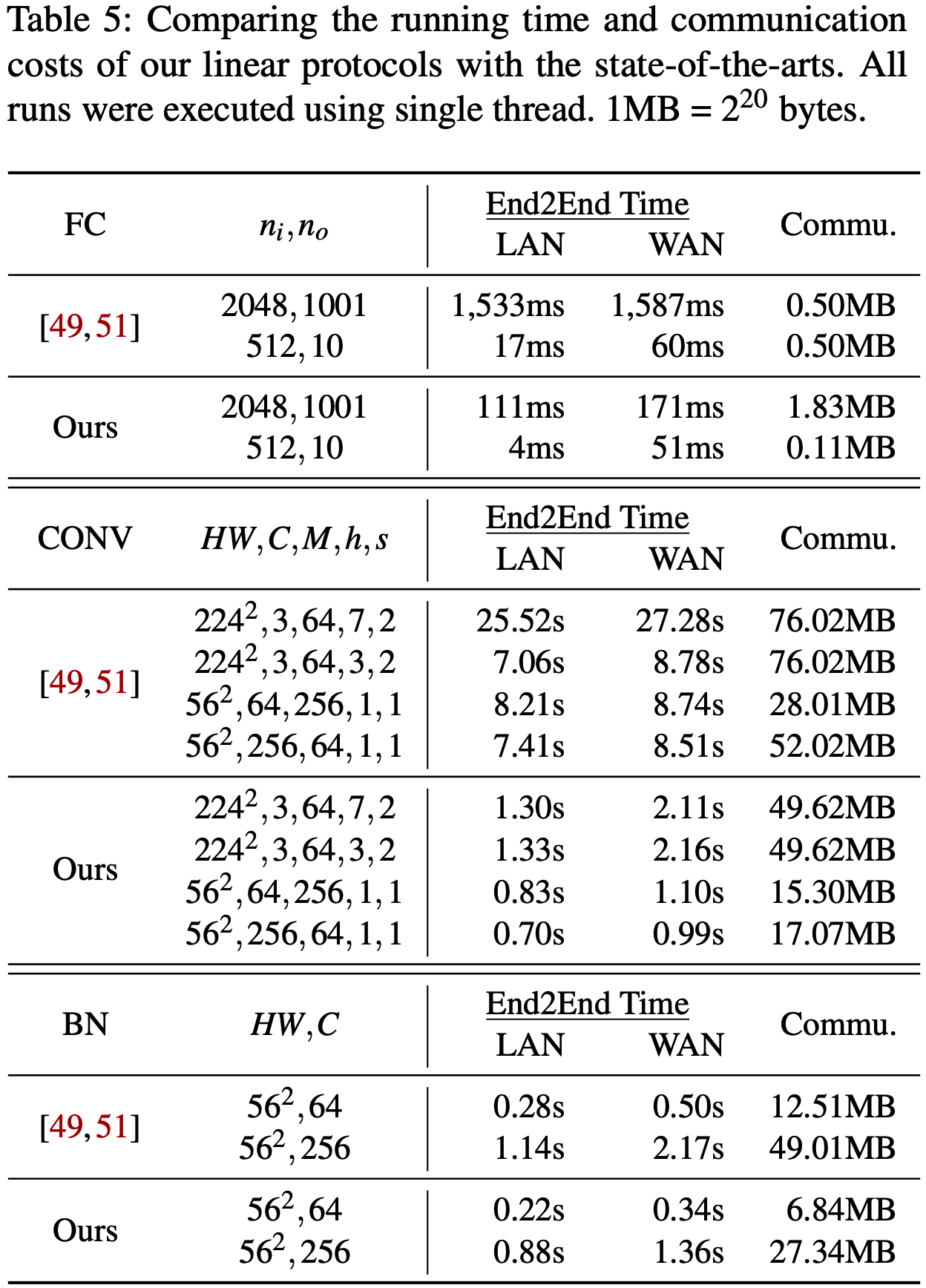
    image-20220228102647861

    非线性函数对比: 单线程下, 本文的所有非线性协议通信开销低10倍以上.

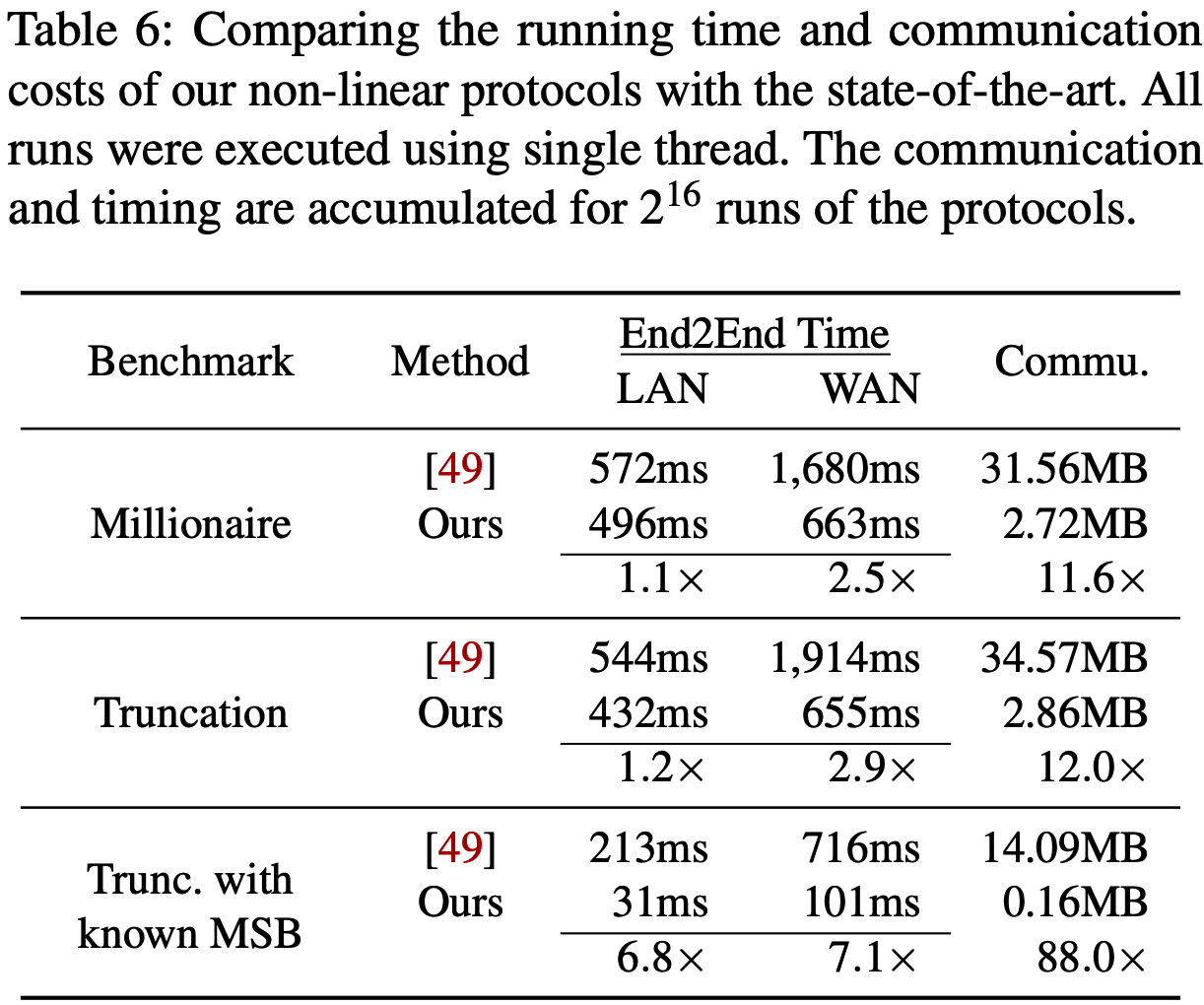
    image-20220228104153836

    与DELPHI5对比: Cheetah计算快1个量级, 通信低2个量级.

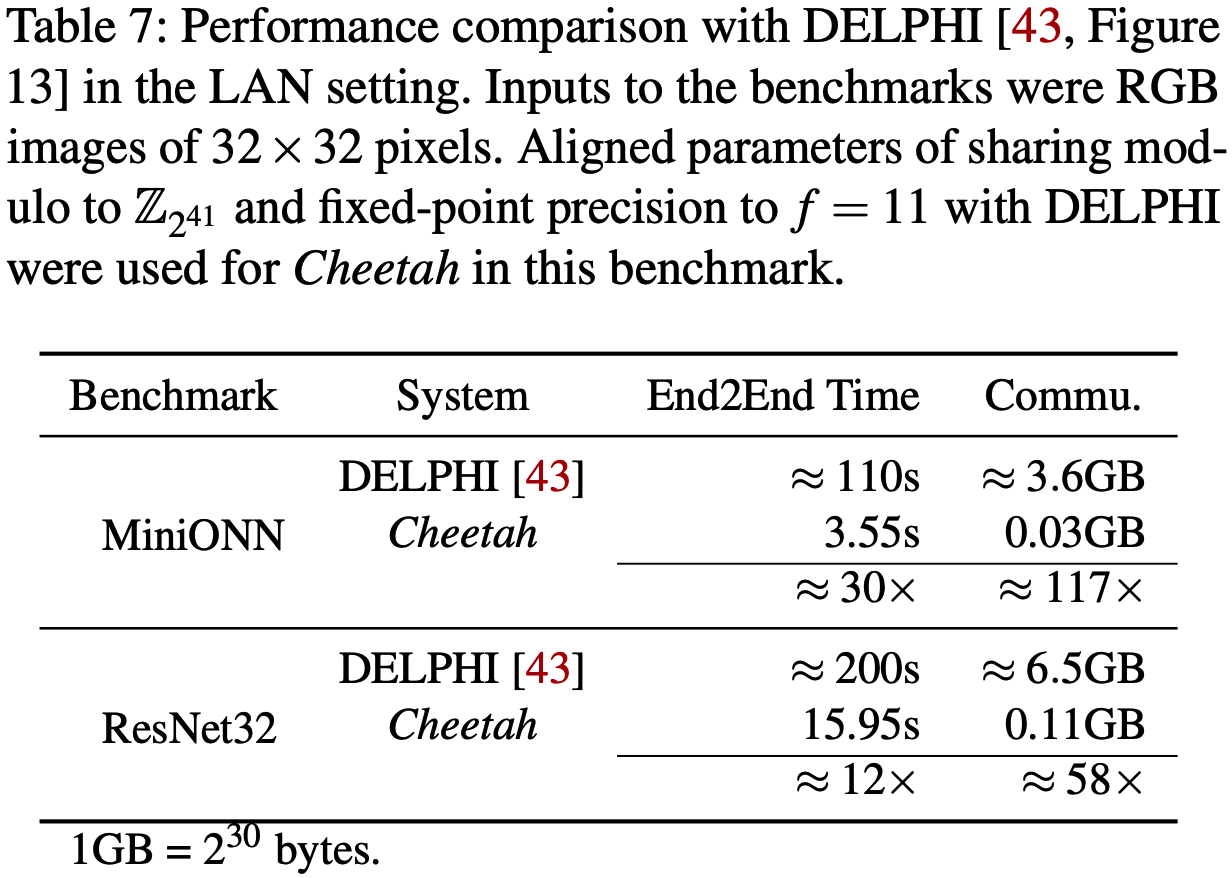
    image-20220228112416461

    与CrypTFlow2对比: 即使在WAN环境下, Cheetah求解SqueezeNet, ResNet50, DenseNet121耗时不到3分钟. 端到端时间方面, Cheetah比\(SCI_\mathsf{HE}\)快2~5倍.

    与SecureQ84对比: 文章还引入了3PC推理框架SecureQ8进行了对比, LAN下SecureQ8比Cheetah快3~4倍, 但WAN下由于通信较少, Cheetah比SecureQ8快2~3倍.

    image-20220228112818099

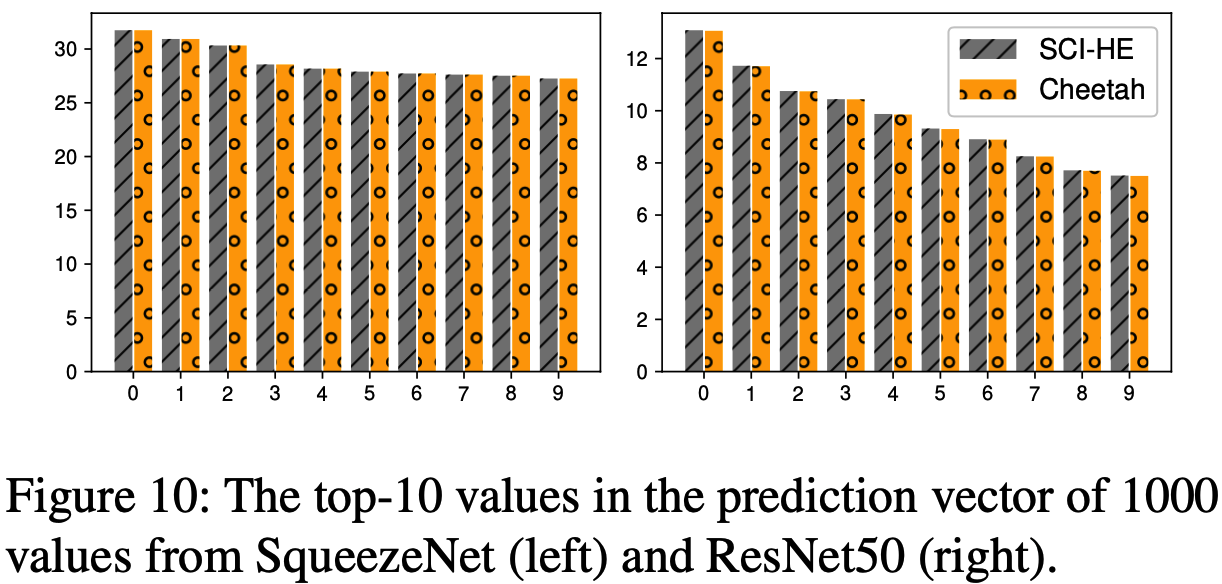
    文章还对近似截断协议的有效性进行了实验, 结果发现对于所有实验图片, Cheetah输出标签向量几乎与\(SCI_\mathsf{HE}\)相同, 定点数计算的预测准确度也与相应的浮点数计算的预测准确度相匹配, 因此对2PC-NN来说, Cheetah是有效的.

    image-20220228124532463

    总结

    Cheetah提供了一个高度优化的2PC-NN推理架构, WAN设定下, 在不到2.5分钟的时间内对ResNet50模型进行安全推理, 消耗2.3GB的通信量, 非常高效, 适合大规模神经网络训练推理, 是目前最好的2PC-NN工作之一.

    总体而言, 本文的亮点有以下几点:

    • 卷积和矩阵向量乘法中涉及的同态rotation操作是基于格的HE方案的性能瓶颈之一, 本文通过构造映射巧妙地消除了同态rotation运算, 也避免了使用SIMD, 加快了同态运算的效率;
    • 基于HE的协议可以直接接受\(\mathbb Z_{2^\ell}\)的秘密份额, 而不局限于\(\mathbb Z_p\), 避免了额外的计算和通信开销;
    • 本文使用了基于VOLE类型的OT扩展协议来构造高效、精简的非线性计算协议, 如截断、比较协议等, 极大降低了安全推理的计算和通信开销.

    参考文献

    1. Elette Boyle,Geoffroy Couteau,Niv Gilboa,Yuval Ishai, Lisa Kohl, Peter Rindal, and Peter Scholl. Efficient two-round OT extension and silent non-interactive secure computation. In CCS, pages 291–308, 2019. ↩

    2. Kang Yang, Chenkai Weng, Xiao Lan, Jiang Zhang, and Xiao Wang. Ferret: Fast extension for correlated OT with small communication. In CCS, pages 1607–1626, 2020. ↩ ↩2

    3. Geoffroy Couteau, Peter Rindal, and Srinivasan Raghuraman. Silver: Silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes. In CRYPTO, pages 502–534, 2021. ↩ ↩2

    4. Anders P. K. Dalskov, Daniel Escudero, and Marcel Keller. Secure evaluation of quantized neural networks. Proc. Priv. Enhancing Technol., 2020(4):355–375, 2020. ↩ ↩2

    5. Pratyush Mishra, Ryan Lehmkuhl, Akshayaram Srini- vasan, Wenting Zheng, and Raluca Ada Popa. DELPHI: A cryptographic inference service for neural networks. In USENIX, pages 2505–2522, 2020. ↩


    本文标题:     Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference
    本文作者: 云中雨雾
    本文链接: https://weiviming.github.io/16460285618722.html
    本站文章采用 知识共享署名4.0 国际许可协议进行许可
    除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
    最后编辑时间: 2022-02-28T14:09:21+08:00