云中雨雾

    SWIFT: Super-fast and Robust Privacy-Preserving Machine Learning

    2022/02/15 20:02 下午 标签: #隐私保护机器学习

    2022年元旦初更USENIX Security'21上的一篇文章SWIFT: Super-fast and Robust Privacy-Preserving Machine Learning, 原文链接如下: https://arxiv.org/abs/2005.10296.

    Abstract

    SWIFT是一个环\(\mathbb Z_{2^{64}},\mathbb Z_2\)上基于秘密共享的高效、恶意安全的3PC/4PC隐私保护机器学习框架, 在诚实大多数设定中(至多只有一个恶意服务器)实现了输出可达性(GOD), 非常适用于安全外包计算(SOC)范式, 能让用户积极参与计算而不需担心拒绝服务. SWIFT与BLAZE一样快, 但后者只实现了公平性. 当SWIFT从三方扩展到四方时, 与4PC具备公平性的Trident一样快, 且比4PC具备鲁棒的FLASH框架快2倍. 在WAN环境中计算域为\(\mathbb Z_{2^{64}}\)的情况下, 文章对流行的ML算法和DNN进行了基准测试, 证明了SWIFT的实用性. 对于DNN, 实验结果证明本文的方案提升了安全性保障, 不会为3PC带来额外开销, 同时还为4PC提升了2倍性能.

    Introduction

    只实现中止安全性的MPC协议不能满足安全外包计算的要求, 因为用户可能无法获得输出, 导致用户的参与度降低, 因此实现输出可达性/鲁棒性的MPC协议对安全外包计算来说是至关重要的. 为了提高效率, 许多PPML方案采用了offline-online范式来设计MPC协议. 此外, 为了进一步提升效率, 充分利用CPU架构的特性, 多数MPC方案的计算域都建立在二次幂环上, 如\(\mathbb Z_{2^{32}}, \mathbb Z_{2^{64}}\)等.

    总的来说, 本文的主要贡献如下:

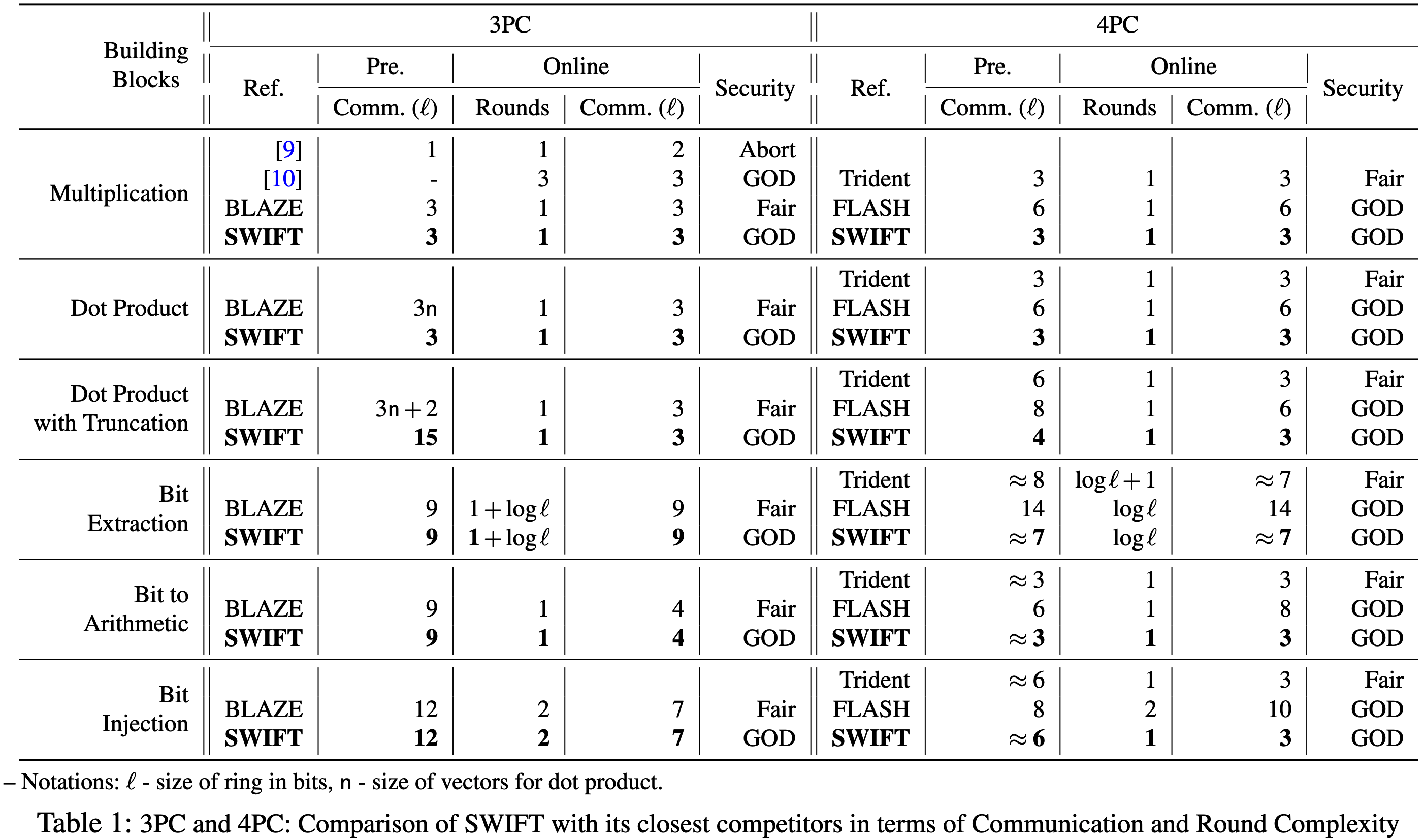
    1. 鲁棒的3PC/4PC框架: SWIFT的3PC框架的亮点之一是鲁棒的点积协议的(均摊)通信成本与向量大小无关. 对于不同的组件, SWIFT与只实现公平性(Fairness)的BLAZE在通信量、通信轮次等方面的比较见表1.
    2. SWIFT的PPML模块可用于LR, SVM, BNN的训练和推理.
    3. SWIFT实现GOD的关键在于本文引入的联合消息传递(Joint Message Passing, JMP)原语, 它允许两个服务器将其共有的消息中继(relay)给第三个服务器验证消息的一致性, 要么中继成功, 要么识别出诚实计算的服务器, 然后诚实服务器作为可信第三方(TTP)来完成明文计算.
    4. 为重构协议引入了一个超快的在线阶段, 通信轮次比BLAZE提升了4倍.

    image-20211229093519029

    此外, 文章还指出了Fantastic Four中存在的一些问题. Fantatstic Four首次提出了隐私鲁棒性(Private Robustness), 作者认为它是GOD的一种变体, 其目的是防止诚实计算方获得用户的隐私输入, 从而在将来变成恶意方时滥用用户隐私输入信息. 但本文指出, 尽管在隐私鲁棒性设定下诚实方不会从协议中学习到用户输入, 但不能阻止敌手向诚实方泄漏他的视图. 在这种情况下, 若诚实方未来变成恶意方, 它可以结合敌手的视图来获得用户的输入. 此外, Fantastic Four中隐私鲁棒性的概念不满足FaF安全性(Friends-and-Foes Security[5]), 在FaF安全性中, 除了传统的腐化方视图需要模拟外, 还要求模拟诚实方的视图, 但Fantastic Four中没有对协议进行相关分析. 最后, Fantastic Four在排除潜在的腐化方时, 需要重新进行计算, 这将导致通信量增加, 降低了效率.

    1. 不能阻止敌手在诚实方变成恶意方之后泄漏敌手的视图从而获取用户输入;
    2. 隐私鲁棒性概念不满足FaF安全性, 后者要求除模拟腐化方视图外, 还需模拟诚实方的视图;
    3. 排除潜在腐化方之后需要重新进行计算, 通信成本增大, 效率降低.

    Preliminaries

    服务器代理模式, 静态恶意敌手至多腐化一个计算服务器, 仅在3PC的情况下存在一个广播信道. 服务器之间通过一次性密钥设定生成用于PRF的预分享随机密钥, 用于生成相关随机性.

    计算域: 布尔域\(\mathbb Z_2\), 算术环为\(\mathbb Z_{2^{64}}\), 数据长度为\(\ell=64\)bits, 精度\(x=13\)bits, 整数部分长度为\(\ell-x-1=40\)bits.

    符号说明: \(\mathsf x_i\)为向量\(\vec{\mathbf x}\)的第\(i\)个元素. 对于长为\(\ell\)的数\(v\), \(v[i]\)表示第\(i\)个位置的比特. 对于比特\(b\in\{0,1\}\), 记\(b^\mathsf R\)为它在二次幂环\(\mathbb Z_{2^\ell}\)上的等价取值, 即\(\mathsf{LSB}(b^\mathsf R)=1\), 其余比特位置为0. 参与方集合记为\(\mathcal P\).

    Robust 3PC and PPML

    Secret Sharing Semantics

    文章中使用了如下三种分享语义:

    • \([\cdot]\)-sharing: 两方下的加法秘密共享, 秘密\(v=[v]_1+[v]_2\), \(P_s\)持有\([v]_s\), \(s\in\{1,2\}\).
    • \(\langle\cdot\rangle\)-sharing: 三方下的复制秘密共享, 秘密\(v=v_0+v_1+v_2\), \(P_s\)拥有\((v_s,v_{(s+1)\%3}), s\in\{0,1,2\}\).
    • \([\![\cdot]\!]\)-sharing: 三方下的复制秘密共享, 设秘密为\(v\), \(P_1,P_2\)分别持有\(\alpha_v\in\mathbb Z_{2^\ell}\)的\([\cdot]\)份额, 存在\(\beta_v,\gamma_v\in\mathbb Z_{2^\ell}\), \(\beta_v=v+\alpha_v\), \(P_0\)持有\(([\alpha_v]_1,[\alpha_v]_2,\beta_v+\gamma_v)\), \(P_s\)持有\(([\alpha_v]_s,\beta_v,\gamma_v)\), 其中\(s\in\{1,2\}\). 在这个分享语义中, 任意一方无法重构\(v\), 但任意两方可以.

    以上三种秘密共享方案都满足线性性, 因此, 它们的加法和常量积的计算是非交互的.

    Joint Message Passing primitive

    引入的联合消息传递(Joint Message Passing, JMP)原语允许两个服务器将其共有的消息中继(relay)给第三个服务器验证消息的一致性, 要么中继验证成功, 要么识别出诚实计算的服务器, 然后, 将诚实服务器作为可信第三方(TTP)来完成相关计算(明文计算). 在均摊意义下, JMP对于一个\(\ell\)个元素的消息, 只产生\(\ell\)个元素的通信.

    对于\(s\in\{i,j,k\}\), \(P_s\)将\(b_s=0\), 作为不一致标志比特. 当\(P_k\)收到不一致的消息对\((v,\mathsf{H}(v^*))\)时, 设定\(b_k=1\), 并将\(b_k\)发送给\(P_i,P_j\), 由这两方通过交换不一致标志比特相互进行交叉检验, 若从\(P_k\)收到的或者从其他发送方接收到的比特为1, 则这两方将自己的不一致标志比特设定为1. 当服务器的不一致标志比特为1时, 服务器会广播值的Hash结果. \(P_k\)的值来自它从\(P_i\)接收到的值. 接下来按照具体协议来选出合适的服务器当做TTP, 三方下JMP的理想功能如图1, 协议如图2. 容易验证协议是正确的. 下文中为简便起见, 称\(P_i,P_j\) jmp-send \(v\) 给\(P_k\), 是指调用\(\Pi_{\mathsf{jmp}}(P_i,P_j,P_k,v)\).

    为均摊通信开销, 实际应用协议时, JMP的发送阶段随协议调用而执行, 而验证阶段在协议的所有结束后进行, 通过组合验证的方式可让验证只需执行一次. 当验证不通过时则通过TTP的帮助来完成相关计算. JMP的通信1轮, 均摊通信量为\(\ell\)比特.

    SWIFT12

    3PC Protocols

    Sharing Protocol

    Sharing Protocol \(\Pi_{\mathsf{sh}}\): 允许\(P_i\)生成秘密\(v\)的\([\![\cdot]\!]\)份额. 该协议预处理阶段不需交互, 在线阶段需要2轮通信, 均摊通信量为\(2\ell\)比特.

    Joint Sharing Protocol

    Joint Sharing Protocol \(\Pi_{\mathsf{jsh}}\): 允许\(P_i,P_j\)联合生成它们的共同秘密\(v\)的\([\![\cdot]\!]\)份额. 该协议预处理阶段不许交互, 在线阶段需要1轮通信, 均摊通信量为\(\ell\)比特.

    SWIFT34

    特别地, 当\(P_i,P_j\)知道预处理阶段的\(v\)时, \(\Pi_\mathsf{jsh}\)可以不需要交互: \(\mathcal P\)随机采样\(r\in\mathbb Z_{2^\ell}\), 然后本地按照表2约定他们各自的份额.

    image-20211230145332669

    Multiplication Protocol

    Multiplication Protocol \(\Pi_\mathsf{mult}\): 给定\([\![x]\!],[\![y]\!]\), 允许\(\mathcal P\)计算得到\(z=xy\)的份额\([\![z]\!]\).

    首先给出半诚实安全下的乘法协议(与BLAZE相同): 在预处理阶段, \(P_0,P_1\)随机选取\([\alpha_z]_1\), \(P_0,P_2\)随机选取\([\alpha_z]_2\), \(P_1,P_2\)随机选取\(\gamma_z\). \(P_0\)本地计算\(\Gamma_{xy}=\alpha_x\alpha_y\), 并为\(P_1,P_2\)生成相同的\([\cdot]\)份额. 对于\(j\in{1,2}\), 在线阶段\(P_j\)本地计算\([\beta_z]_j=(j-1)\beta_x\beta_y-\beta_x[\alpha_y]_j-\beta_y[\alpha_x]_j+[\Gamma_{xy}]_j+[\alpha_{z}]_j\), 并互相交换重构\(\beta_z\). 然后\(P_1\)发送\(\beta_z+\gamma_z\)给\(P_0\), 完成半诚实安全的协议. 协议的正确性在于如下等式

    \[\begin{aligned} xy=z=\beta_z-\alpha_z\Rightarrow\beta_z&=z+\alpha_z=xy+\alpha_z=(\beta_x-\alpha_x)(\beta_y-\alpha_y)+\alpha_z\\ &=\beta_x\beta_y-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z. \end{aligned} \]

    与BLAZE类似, 在恶意安全下, 需要考虑如下几个问题:

    问题1. 当\(P_0\)被腐化时, 所计算的\(\Gamma_{xy}\neq\alpha_x\alpha_y\);

    问题2. 当\(P_1\)或\(P_2\)被腐化时, 可能发送错误的\([\beta_z]\)份额给另一方, 导致重构的\(\beta_z\)是错误的;

    问题3. 当\(P_1\)被腐化时, 在线阶段发送给\(P_0\)的\(\beta_z+\gamma_z\)可能是不正确的.

    BLAZE中的恶意安全的乘法方案仅是中止安全的(Security with abort), 在SWIFT中处理方式与BLAZE不同.

    对于问题3, SWIFT框架在计算\(\beta_z\)后, 通过\(P_1,P_2\) jmp-send \(\beta_z+\gamma_z\)给\(P_0\)来解决.

    对于问题2, 我们首先介绍BLAZE中的处理方式. 在BLAZE中, 让\(P_0\)基于\(\beta_x,\beta_y\)计算\(\beta_z\)进行验证. 令\(\chi=\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}\), \(P_0\)通过\(\beta_x+\gamma_x,\beta_y+\gamma_y,\alpha_x,\alpha_y,\alpha_z,\Gamma_{xy}\)可以计算如下等式:

    \[\begin{aligned} \beta_z^*&=-(\beta_x+\gamma_x)\alpha_y-(\beta_y+\gamma_y)\alpha_x+2\Gamma_{xy}+\alpha_z\\ &=(-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy})\\ &=(\beta_z-\beta_x\beta_y)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy})\\ &=(\beta_z-\beta_x\beta_y)-\chi. \end{aligned} \]

    若\(P_0\)可以得到\(\chi\), 则它可以发\(\beta_z^*+\chi\)给\(P_1\)和\(P_2\), 由\(P_1\)和\(P_2\)通过计算\(\beta_z-\beta_x\beta_y\overset{?}{=}\beta_z^*+\chi\)来验证\(\beta_z\)的正确性. 但当\(P_0\)是腐化方时, 让\(P_0\)得到\(\chi\)是不安全的. 为此, \(P_1,P_2\)通过关联随机性共同选取随机数\(\psi\)作为茫化因子, 然后令\(\chi=\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi, \beta_z^*=(\beta_z-\beta_x\beta_y+\psi)-\chi\). 此时让\(P_0\)得到的是\(\chi+\psi\), 然后\(P_1,P_2\)计算\(\beta_z-\beta_x\beta_y+\psi\overset{?}{=}\beta_z^*+\chi\)验证\(\beta_z\)的正确性. 接下来, 如何确保\(P_0\)在诚实时计算了正确的\(\chi\)? BLAZE将该问题规约到一个Beaver triple. 注意到对于\(j\in\{1,2\}\), \(P_j\)可以本地计算\([\chi]_j=\gamma_x[\alpha_y]_j+\gamma_y[\alpha_x]_j-[\Gamma_{xy}]+[\psi]_j\), 其中\([\psi]_j\)由两方通过关联随机性生成. 为了验证\(P_0\)正确计算了正确的\(\chi\), 我们可以利用如下关系: 若\(d=\gamma_x-\alpha_x,e=\gamma_y-\alpha_y, f=(\gamma_x\gamma_y+\psi)-\chi\)满足\(f=de\), 当且仅当正确计算了\(\chi\). 这是因为

    \[\begin{aligned} de&=(\gamma_x-\alpha_x)(\gamma_y-\alpha_y)=\gamma_x\gamma_y-\gamma_x\alpha_y-\gamma_y\alpha_x+\Gamma_{xy}\\ &=(\gamma_x\gamma_y+\psi)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi)\\ &=(\gamma_x\gamma_y+\psi)-\chi=f. \end{aligned} \]

    于是, \(\chi\)的正确性规约到\((d,e,f)\)是否为Beaver triple.

    对于问题1, 仍可通过规约到判断Beaver triple的方案来解决, 这是因为若\(P_0\)的份额为\(\Gamma_{xy}+\Delta\), 则\(de=f+\Delta\neq f\).

    现在回到SWIFT的解决方案中. 首先, SWIFT不依赖于\(P_0\)验证信息\(\beta_z^*+\chi\), 如此当\(P_0\)被腐化时协议不会中止. 与直接让\(P_0\)得到\(\beta_z^*\)不同, 在SWIFT中让\(\{P_0,P_1\}\)得到\([\beta_z^*]_1\), \(\{P_0,P_2\}\)得到\([\beta_z^*]_2\), 然后通过jmp-send发送\([\beta_z^*]_i\)给第三方服务器计算\(\beta_z^*\). 由于每个参与方集合中至少存在一个诚实参与方, 因此可确保\(\beta_z^*\)是正确的, \(P_1,P_2\)直接用它来计算\(\beta_z=\beta_x\beta_y+\psi+\beta_z^*\). SWIFT中定义

    \[\chi=\gamma_x\alpha_y+\gamma_y\alpha_x+\Gamma_{xy}-\psi, \] \[\begin{aligned} \beta_z^*&=-(\beta_x+\gamma_x)\alpha_y-(\beta_y+\gamma_y)\alpha_x+\alpha_z+\chi\\ &=(-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z)-\psi=\beta_z-\beta_x\beta_y-\psi. \end{aligned} \]

    显然, 给定\([\chi]_i\), \(P_0\)和\(P_i\)可以计算\([\beta_z^*]_i=-(\beta_x+\gamma_x)[\alpha_y]_i-(\beta_y+\gamma_y)[\alpha_x]_i+[\alpha_z]_i+[\chi]_i\). 但还需要解决如下两个问题:

    (1) 如何让\(\{P_0,P_i\}\)得到\([\chi]_i\)?

    (2) \(P_1,P_2\)如何从Beaver triple中提取\(\psi\)?

    类似于BLAZE的方法, 若\(d=\gamma_x+\alpha_x,e=\gamma_y+\alpha_y,f=(\gamma_x\gamma_y+\psi)+\chi\), \((d,e,f)\)是Beaver triple当且仅当\(\chi\)和\(\Gamma_{xy}\)是正确的. 这是因为

    \[\begin{aligned} de&=(\gamma_x+\alpha_x)(\gamma_y+\alpha_y)=\gamma_x\gamma_y+\gamma_x\alpha_y+\gamma_y\alpha_x+\Gamma_{xy}\\ &=(\gamma_x\gamma_y+\psi)+(\gamma_x\alpha_y+\gamma_y\alpha_x+\Gamma_{xy}-\psi)\\ &=(\gamma_x\gamma_y+\psi)+\chi=f \end{aligned} \]

    在预处理阶段中通过使用乘法协议计算上述triple并从\(f\)的份额中提取的\(\psi,\chi\)必然是正确的. 具体而言, (a) 服务器本地得到\(d,e\)的\(\langle\cdot\rangle\)-份额, 如表3; (b) 服务器计算\(f(=de)\)的\(\langle\cdot\rangle\)-份额, 表示为\(f_0,f_1,f_2\), 通过使用高效鲁棒的三方乘法协议\(\Pi_\mathsf{mulPre}\)(图6); (c) 服务器本地提取所需的预处理数据: \([\chi]_2\leftarrow f_0, [\chi]_1\leftarrow f_1, \gamma_x\gamma_y+\psi\leftarrow f_2.\) 将这部分转换为\(\langle\cdot\rangle\)份额的鲁棒乘法协议不需要任何通信, 因为(a)和(c)都是本地计算, 通信开销规约到单次执行乘法协议的开销.

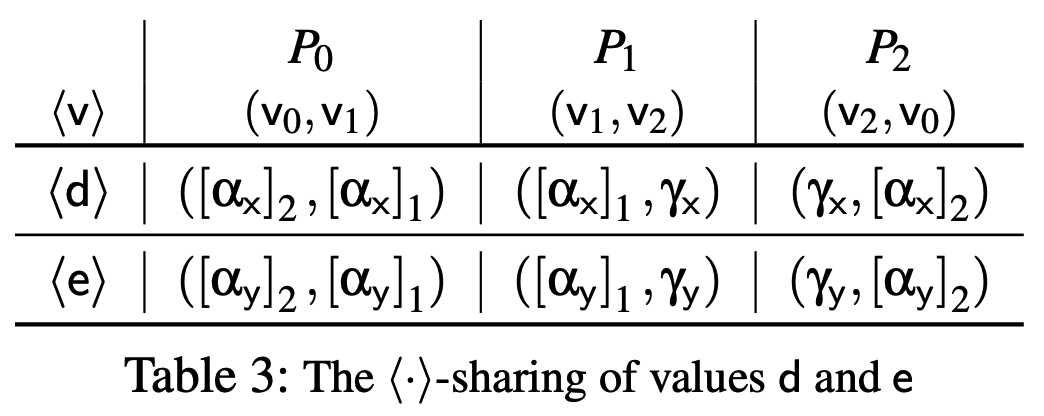
    image-20220101152057914 image-20220101152143461

    根据\(\langle\cdot\rangle\)-sharing, \(P_0,P_1\)得到\(f_1\), 进而得到\([\chi]_1\). 类似地, \(P_0,P_2\)得到\(f_2\), 进而得到\([\chi]_2\). 最后, \(P_1,P_2\)得到\(f_2\), 进而可以计算\(\psi=f_2-\gamma_x\gamma_y\). 这样两个问题都解决了.

    完整的乘法协议见图5. 预处理阶段的均摊通信开销为1轮, \(3\ell\)比特, 在线阶段的均摊开销为\(3\ell\)比特.

    image-20220101170416469

    Reconstruction Protocol

    Reconstruction Protocol \(\Pi_\mathsf{rec}\): 允许服务器鲁棒地从份额\([\![v]\!]\)重构秘密\(v\). 重构协议主要使用了承诺. 通信轮次为1, 通信量为\(6\ell\)比特.

    image-20220101175841125

    The Complete 3PC Protocol

    使用以上子协议实现GOD的3PC协议如下. 总的来说, 如果某个参与方存在任何恶意行为, 协议都能通过jmp选出一个TTP, 所有参与方将输入发给TTP进行明文计算. SWIFT证明的是标准的real-ideal world-based Security, 因为FaF安全的鲁棒3PC协议已经被证明是不可能实现的.

    image-20220101185340871

    Building Blocks for PPML using 3PC

    Input Sharing and Output Reconstruction in SOC Setting

    Input Sharing Protocol \(\Pi_\mathsf{sh}^\mathsf{SOC}\): 在SOC场景下允许用户三个服务器之间生成秘密输入\(v\)的\([\![\cdot]\!]\)-sharing的份额.

    Output Reconstruction Protocol \(\Pi_\mathsf{rec}^\mathsf{SOC}\): 在SOC场景下允许服务器向用户重构秘密\(v\).

    在以上协议中, 若某处确定了TTP, 则服务器将通知用户TTP身份, 用户将明文形式的输入发送给TTP进行计算函数输出, 然后将结果返回给用户.

    image-20220102112432092

    MSB Extraction

    MSB Extraction Protocol \(\Pi_\mathsf{bitext}\): 给定\(v\)的算术分享\([\![v]\!]\), 协议允许服务器计算\(v\)的最高有效位的布尔分享. SWIFT使用了ABY3的优化的2-输入并行前缀加法器布尔电路[optimized 2-input Parallel Prefix Adder (PPA) boolean circuit]. PPA电路由\(2\ell-2\)个AND门和\(\log\ell\)的乘法深度.

    令\(v_0=\beta_v,v_1=-[\alpha_v]_1, v_2=-[\alpha_v]_2\), 则\(v=v_0+v_1+v_2\). 服务器首先根据表4本地计算\(v_0,v_1,v_2\)的每个比特相应的布尔分享. ABY3中将\(v=v_0+v_1+v_2\)表示为\(v=2c+s\), 其中\(\mathsf{FA}(v_0[i],v_1[i],v_2[i])\rightarrow(c[i],s[i]), i\in\{0,1,\cdots,\ell-1\}\), 这里的\(\mathsf{FA}\)代表一个全加电路, \(s\)代表比特的和, \(c\)代表进位比特. 总之, 服务器并行运行\(\ell\)次\(\mathsf{FA}\)来计算\([\![c]\!]^\mathsf B,[\![s]\!]^\mathsf B\). \(\mathsf{FA}\)是独立运行的, 需要1轮通信, 使用优化后的FFA电路计算最终结果为\(\mathsf{msb}(2[\![c]\!]^\mathsf B+[\![s]\!]^\mathsf B)\).

    \(\Pi_\mathsf{bitext}\)在预处理阶段需要的通信量为\(9\ell-6\)比特, 通信轮次为\(\log\ell+1\)轮, 在线阶段均摊通信量为\(9\ell-6\)比特.

    image-20220102132426325

    Bit to Arithmetic Conversion

    Bit to Arithmetic Conversion Protocol \(\Pi_\mathsf{bit2A}\): 给定比特\(b\)的布尔分享\([\![b]\!]^\mathsf B\), 该协议允许服务器计算算术分享\([\![b^\mathsf R]\!]\). 和BLAZE一样, 原理是先在预处理阶段生成\(\alpha_b^\mathsf R=([\alpha_b]_1\oplus[\alpha_b]_2)^\mathsf R=[\alpha_b]_1^\mathsf R+[\alpha_b]_2^\mathsf R-2[\alpha_b]_1^\mathsf R[\alpha_b]_2^\mathsf R\), 然后在线阶段计算\(b^\mathsf R=(\beta_b\oplus\alpha_b)^\mathsf R=\beta_b^\mathsf R+\alpha_b^\mathsf R-2\beta_b^\mathsf R\alpha_b^\mathsf R\). 具体协议如下图. 该协议预处理阶段的均摊通信量为\(9\ell\)比特, 在线阶段需要1轮, \(4\ell\)比特通信量.

    image-20220102155339680

    Bit Injection

    Bit Injection Protocol \(\Pi_\mathsf{BitInj}\): 给定比特\(b\)的二进制分享\([\![b]\!]^\mathsf{B}\)和\(v\)的算术分享\([\![v]\!]\), 该协议计算\([\![bv]\!]\). 原理是先通过\(\Pi_\mathsf{Bit2A}\)将\([\![b]\!]^\mathsf B\)转换为\([\![b]\!]\), 然后再通过\(\Pi_\mathsf{mult}\)计算\([\![bv]\!]=[\![b]\!]\cdot[\![v]\!]\). 预处理阶段均摊通信量为\(12\ell\)比特, 在线阶段需要2轮, 均摊通信量为\(7\ell\)比特.

    Dot Product

    Dot Product Protocol \(\Pi_\mathsf{dotp}\): 给定长度为\(n\)的向量\([\![\vec{\mathbf{x}}]\!]\)和\([\![\vec{\mathbf{y}}]\!]\), 协议允许服务器鲁棒地生成\(z=\vec{\mathbf{x}}\odot\vec{\mathbf{y}}\)的\([\![\cdot]\!]\)-sharing份额\([\![z]\!]\). SWIFT中借鉴了BLAZE的方法, 使得协议在线阶段的通信量与向量长度\(n\)无关.

    \(z=\vec{\mathbf{x}}\odot\vec{\mathbf{y}}\)是形式为\(z_i=x_iy_i,i\in[n]\)的\(n\)个并行乘法, 再将结果累加在一起. 令\(\beta_z^*=\sum_{i=1}^n\beta_{z_i}^*\), 则

    \[\beta_z^*=-\sum_{i=1}^n(\beta_{x_i}+\gamma_{x_i})\alpha_{y_i}-\sum_{i=1}^n(\beta_{y_i}+\gamma_{y_i})\alpha_{x_i}+\alpha_z+\chi, \]

    其中\(\chi=\sum_{i=1}^n(\gamma_{x_i}\alpha_{y_i}+\gamma_{y_i}\alpha_{x_i}+\Gamma_{x_iy_i}-\psi_i)\).

    点积协议的在线阶段处理方式与乘法协议类似. \(P_0, P_1\)本地计算\([\beta_z^*]_1\)并通过jmp-send发送给\(P_2\). 类似地, \(P_0,P_2\)本地计算\([\beta_z^*]_2\)并通过jmp-send发送给\(P_1\). 然后\(P_1\)和\(P_2\)重构\(\beta_z^*=[\beta_z^*]_1+[\beta_z^*]_2\)并计算\(\beta_z=\beta_z^*+\sum_{i=1}^n\beta_{x_i}\beta_{y_i}+\psi\). 最后, \(P_1,P_2\)通过jmp-send发送\(\beta_z+\gamma_z\)给\(P_0\).

    下面介绍如何通过黑盒(black-box)方式在预处理阶段让服务器获得点积协议所需的\((\chi,\psi)\).

    令\(\vec{\mathbf{d}}=[d_1,\cdots,d_n], \vec{\mathbf{e}}=[e_1,\cdots,e_n]\), 其中\(d_i=\gamma_{x_i}+\alpha_{x_i}, e_i=\gamma_{y_i}+\alpha_{y_i}, i\in[n]\), 如此

    \[\begin{aligned} f&=\vec{\mathbf{d}}\odot\vec{\mathbf{e}}=\sum_{i=1}^nd_ie_i=\sum_{i=1}^n(\gamma_{x_i}+\alpha_{x_i})(\gamma_{y_i}+\alpha_{y_i})\\ &=\sum_{i=1}^n(\gamma_{x_i}\gamma_{y_i}+\psi_{i})+\sum_{i=1}^n\chi_i=\sum_{i=1}^n(\gamma_{x_i}\gamma_{y_i}+\psi_{i})+\chi\\ &=\sum_{i=1}^n(\gamma_{x_i}\gamma_{y_i}+\psi_{i})+[\chi]_1+[\chi]_2=f_2+f_1+f_0, \end{aligned} \]

    其中\(f_2=\sum_{i=1}^n(\gamma_{x_i}\gamma_{y_i}+\psi_i), f_1=[\chi]_1,f_2=[\chi]_2\).

    使用以上关系, 预处理阶段的处理方式如下: \(P_0,P_1\)随机选取\([\alpha_z]_1\), \(P_0,P_2\)随机选取\([\alpha_z]_2\), \(P_1,P_2\)随机选取\(\gamma_z\). 服务器类似于乘法协议一样准备\(\langle\vec{\mathbf{d}}\rangle, \langle\vec{\mathbf{e}}\rangle\), 并将其作为图12的鲁棒3PC点积协议\(\Pi_\mathsf{dotPre}\)的输入, 计算\(\langle f \rangle\), 这里的\(f=\vec{\mathbf{d}}\odot \vec{\mathbf{e}}\). 给定\(\langle f \rangle\), \(\psi\)和\([\chi]\)的提取方式如下:

    \[\psi=f_2-\sum_{i=1}^n\gamma_{x_i}\gamma_{y_i}, [\chi]_1=f_1, [\chi]_2=f_0. \]

    如此根据\(\langle\cdot\rangle\)-sharing语义, \(P_1,P_2\)可以得到\(f_2\), 进而得到\(\psi\), 同时\(P_0,P_1\)均可得到\(f_1\)进而得到\([\chi]_1\), \(P_0,P_2\)均可得到\(f_0\)进而得到\([\chi]_2\).

    完整的点积计算协议如下图11. 预处理阶段的均摊通信量为\(3\ell\)比特, 在线阶段需要1轮, 均摊通信量为\(3\ell\)比特.

    对于图12的具体协议, SWIFT中通过半诚实点积协议进行实例化, 并在验证阶段验证正确性, 通过适当地设定验证阶段参数可以给出一个均摊通信成本与向量长度几乎无关的\(\Pi_\mathsf{dotpPre}\). 见文章的附录B.

    SWIFT1211

    Truncation

    在定点数表示形式下进行乘法运算需要考虑截断问题, 设定点精度为\(d\). 与ABY3的截断方案类似, 服务器运行\(\Pi_\mathsf{trgen}\)协议生成截断对\(([r],[\![r]\!]^d)\), 其中\(r\)是随机环元素, \(r^d\)是\(r\)的截断结果, 即\(r^d=r/2^d\). 给定\((r,r^d)\), 要截断的值\(v\), 截断结果表示为\(v^d=(v-r)^d+r^d\). 为了从\((r,r^d)\)的布尔分享中获得算术分享, 与ABY3需要多轮通信的方法不同, SWIFT中使用的是Trident中的方案, \(\Pi_\mathsf{trgen}\)实现布尔分享到算术分享的隐式转换只需2个点积运算的开销.

    下面介绍如何生成所需的截断对\(([r],[\![r]\!]^d)\). \(P_0,P_1\)随机采样\(r_1\), \(P_0,P_2\)随机采样\(r_2\). 设\(r\)的第\(i\)比特表示为\(r[i], i\in\{0,\cdots,\ell-1\}\), 定义\(r[i]=r_1[i]\oplus r_2[i]\), 则\(r^d[i]=r_1[i+d]\oplus r_2[i+d], i\in\{0,\cdots,\ell-d-1\}\). 更进一步地, 有

    \[\begin{aligned} r&=\sum_{i=0}^{\ell-1}2^ir[i]=\sum_{i=0}^{\ell-1}2^i(r_1[i]\oplus r_2[i])\\ &=\sum_{i=0}^{\ell-1}2^i((r_1[i])^\mathsf R+(r_2[i])^\mathsf R-2(r_1[i])^\mathsf R\cdot(r_2[i])^\mathsf R)\\ &=\sum_{i=0}^{\ell-1}2^i((r_1[i])^\mathsf R+(r_2[i])^\mathsf R)-\sum_{i=0}^{\ell-1}(2^{i+1}(r_1[i])^\mathsf R)\cdot(r_2[i])^\mathsf R. \end{aligned} \]

    类似地, 对于\(r^d\), 有

    \[r^d=\sum_{i=d}^{\ell-1}2^{i-d}((r_1[i])^\mathsf R+(r_2[i])^\mathsf R)-\sum_{i=d}^{\ell-1}(2^{i-d+1}(r_1[i])^\mathsf R)\cdot(r_2[i])^\mathsf R. \]

    服务器通过表2的形式非交互生成\(r_1,r_2\)的每个比特的算术\([\![\cdot]\!]\)份额. 然后执行两次\(\Pi_\mathsf{dotp}\)计算\(A=\sum_{i=d}^{\ell-1}(2^{i-d+1}(r_1[i])^\mathsf R)\cdot(r_2[i])^\mathsf R\)的份额\([\![A]\!]\)和\(B=\sum_{i=0}^{\ell-1}(2^{i+1}(r_1[i])^\mathsf R)\cdot(r_2[i])^\mathsf R\)的份额\([\![B]\!]\). 然后服务器各自根据以上两条等式本地计算\((r,r^d)\)的\([\![\cdot]\!]\)份额.

    然而服务器需要的并非\([\![r]\!]\)份额而是\([r]\)份额. 将\([\![r]\!]\)份额本地转换为\([r]\)份额的方式如下: 设\((\alpha_r,\beta_r,\gamma_r)\)是\([\![r]\!]\)份额的相应参数. 因为\(P_0\)知道明文的\(r\)和\(\alpha_r\), 因此可以本地计算\(\beta_r=r+\alpha_r\). 然后\(P_0,P_1\)令\([r]_1=-[\alpha_r]_1\), \(P_0,P_2\)令\([r]_2=\beta-[\alpha_r]_2\).

    整个\(\Pi_\mathsf{trgen}\)协议如下, 均摊通信量为\(12\ell\)比特.

    image-20220102220515639

    Dot Product with Truncation

    Dot Product with Truncation Protocol \(\Pi_\mathsf{dotpt}\): 允许服务器对点积计算结果\([\![z]\!]\)进行截断得到\([\![z^d]\!]\). SWIFT中使用了BLAZE中相应的优化方案. 预处理阶段的均摊通信量为\(15\ell\)比特, 在线阶段需要1轮, \(3\ell\)比特的均摊通信量.

    image-20220103113826973

    Secure Comparison

    在FPA表示法下两数比较大小只需通过\(\Pi_\mathsf{bitext}\)协议提取两数差值的最高有效位.

    Activation Functions

    • ReLU函数: \(\mathsf{relu}(v)=\mathsf{max}(0,v)=\bar{b}\cdot v\), 其中\(\bar b=0\Leftrightarrow b=1\Leftrightarrow v<0\), 反之\(\bar b=1\Leftrightarrow b=0\Leftrightarrow v\geq 0\). 因此关键在于抽取\(v\)的符号位, 在\([\![v]\!]\)形式下可以通过\(\Pi_\mathsf{bitext}\)协议生成\([\![b]\!]^\mathsf B\). 而\([\![\bar b]\!]^\mathsf B\)可以令\(\beta_\bar{b}=1\oplus\beta_b\)本地计算求得. 最后将\([\![\bar{b}]\!]^\mathsf B,[\![v]\!]\)作为输入执行一次\(\Pi_\mathsf{BitInj}\)协议即得. 预处理阶段均摊通信量为\(21\ell-6\)比特, 在线阶段需要\(\log \ell+3\)轮, 均摊通信量为\(16\ell-6\)比特.
    • Sigmoid函数: 与SecureML相同, SWIFT通过分段函数来替代Sigmoid函数, 此时\(\mathsf{sig}(v)=\bar{b}_1b_2(v+1/2)+\bar{b}_2\), 其中\(v+1/2<0\Leftrightarrow b_1=1\), \(v-1/2<0\Leftrightarrow b_2=1\). 通过ReLU函数的方法来求解. 预处理阶段均摊通信量为\(39\ell-9\)比特, 在线阶段需要\(\log\ell+4\)轮, 均摊通信量为\(29\ell-9\)比特.

    Maxpool, Matrix Operations and Convolutions

    • Maxpool: 计算长度为\(m\)的向量\(\vec{\mathbf{x}}\)中的最大值. 两两成对进行比较, 并使用\(\Pi_\mathsf{BitInj}\)协议更新最大值.
    • 矩阵乘法: 转化为点积计算.
    • 卷积计算: 与SecureNN相同, 可以转化为矩阵乘法的计算.

    Robust 4PC and PPML

    SWIFT将3PC扩展到4PC, 不再需要调用广播, 点积计算与向量长度无关, 高效的主要原因是4PC的鲁棒JMP4原语\(\mathsf{jmp4}\). 由于4PC的实现原理多数与3PC类似, 因此下面除不同之处外, 不再展开.

    4PC Secret Sharing Semantics

    扩展到4PC的\([\![\cdot]\!]\)-sharing: 对于秘密\(v=\beta_v-[\alpha_v]_1-[\alpha_v]_2\), \(P_0\)的份额为\(([\alpha_v]_1,[\alpha_v]_2,\beta_v+\gamma_v)\), \(P_1\)的份额为\(([\alpha_v]_1,\beta_v,\gamma_v)\), \(P_2\)的份额为\(([\alpha_v]_2,\beta_v,\gamma_v)\), \(P_3\)的份额为\(([\alpha_v]_1,[\alpha_v]_2,\gamma_v)\). 易见, \(P_0,P_1,P_2\)的份额与3PC下的份额相同.

    4PC Joint Message Passing Primitive

    \(\mathsf{jmp4}\)原语允许\(P_i,P_j\)发送消息对\((v,\mathsf{H}(v'))\)给\(P_k\), 当\(P_k\)收到的信息不一致时, 设定不一致标志比特为1, 将服务器\(P_l\)作为TTP再进行相关明文计算. 称\(P_i,P_j\)通过jmp4-send发送\(v\)给\(P_k\)是指调用\(\Pi_\mathsf{jmp4}(P_i,P_j,P_k,v,P_l)\). 该原语比FLASH提出的双向传输(bi-convery)方案快2倍. 具体协议见图16, 在线阶段需要1轮, 均摊通信量为\(\ell\)比特.

    SWIFT1516

    4PC Protocols

    Sharing Protocol

    Sharing Protocol \(\Pi_\mathsf{sh4}\): 在线阶段需要2轮, 当\(P_0,P_1,P_2\)分享秘密时, 均摊通信量为\(2\ell\)比特; 当\(P_3\)需要分享秘密时, 均摊通信量为\(3\ell\)比特.

    image-20220104150347285

    Joint Sharing Protocol

    Joint Sharing Protocol \(\Pi_\mathsf{jsh4}\): 允许服务器\((P_i,P_j)\)联合生成\([\![v]\!]\), 其中\(v\)是\(P_i,P_j\)的共同秘密. 当发现信息存在不一致时, 将没有进行计算的那个服务器选为TTP. 在线阶段, 需要1轮, 当\((P_3,P_s), s\in\{0,1,2\}\)分享时, 均摊通信量为\(2\ell\)比特. 其他情况的均摊通信量为\(\ell\)比特.

    特别地, 若\(v\)是\(P_0,P_1,P_2\)的共同秘密, 那么不需交互即可生成\([\![v]\!]\)份额: 令\([\alpha_v]_1=[\alpha_v]_2=\gamma_v=0, \beta_v=v\).

    若\(v\)是\(P_0,P_3\)的共同秘密, 那么可以只通信1个元素: \(P_0,P_1,P_3\)选取随机数\(r\), 令\([\alpha_v]=r\); \(P_0,P_3\)约定\([\alpha_v]_2=-(r+v)\), 然后jmp4-send发送\([\alpha_v]_2\)给\(P_2\).

    image-20220104162456328

    \(\langle\cdot\rangle\)-sharing Protocol

    某些情况下, \(P_3\)需要在预处理阶段生成\(v\)的\(\langle \cdot\rangle\)-sharing, 其中\(v=v_0+v_1+v_2\), \(P_0\)持有\((v_0,v_1)\), \(P_1\)持有\((v_1,v_2)\), \(P_2\)持有\((v_2,v_0)\), 而\(P_3\)则有\((v_0,v_1,v_2)\). 具体协议\(\Pi_\mathsf{ash4}\)如下图19, 需要2轮, 均摊通信量为\(2\ell\)比特.

    image-20220104172331359

    此外, 服务器可以本地将\(\langle v\rangle\)转换为\([\![v]\!]\), 只需按照下表5的方式约定他们的份额即可. 此时, \([\alpha_v]_1=-v_1, [\alpha_v]_2=-v_0,\beta_v=v_2,\gamma_v=-v_2\).

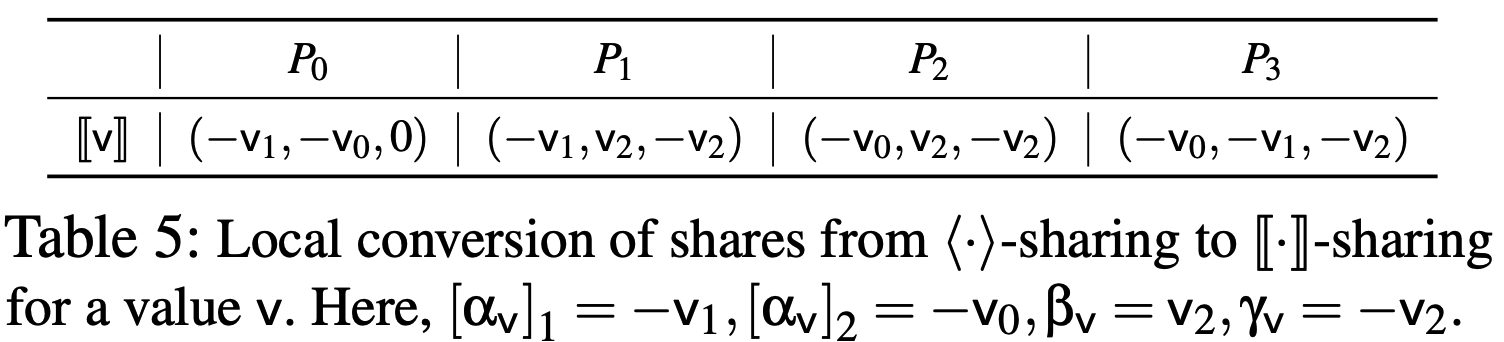
    image-20220104195728881

    Multiplication Protocol

    4PC下\([\![\cdot]\!]\)-sharing的乘法协议\(\Pi_\mathsf{mult4}\). 预处理阶段需要\(3\ell\)比特的均摊通信量, 在线阶段需要1轮, \(3\ell\)比特的均摊通信量.

    image-20220104193501814

    Reconstruction Protocol

    4PC下给定\([\![v]\!]\), 鲁棒地重构\(v\)的协议\(\Pi_\mathsf{rec4}\). 因为每个服务器都只缺少一个份额即可重构, 而该缺失份额其他三个服务器都有, 因此这三个服务器中的其中两个发送该缺失份额, 第三个发送该份额的Hash值以进行一致性检查. 与3PC下的乘法协议相比, 4PC下的乘法协议不需要使用承诺方案. 在线阶段需要1轮, 均摊通信量为\(8\ell\)比特.

    image-20220104195527019

    Building Blocks for PPML using 4PC

    Input Sharing and Output Reconstruction in SOC Setting

    下面将SOC场景中的3PC的输入分享和输出重构协议扩展到4PC. 其核心在于使用了拜占庭协定(Byzantine agreement, BA).

    为了生成用户的输入\(v\)的\([\![\cdot]\!]\)-sharing份额\([\![v]\!]\), 用户从四个服务器中的三个中接收\([\alpha_v]_1,[\alpha_v]_2,\gamma_v\), 以及\(P_0,P_1,P_2\)共同选取的随机数\(r\), 接受其中大多数的那个\(r\). 用户本地计算\(u=v+[\alpha_v]_1+[\alpha_v]_2+\gamma_v+r\), 并发送\(u\)给所有服务器. 服务器执行两轮拜占庭协定接受\(u\)或者\(\perp\).

    拜占庭协定过程如下: 设\(P_i\)接收到的来自用户的值为\(u_i\), 为达成协定, 服务器首先就\(P_i\)收到\(u_i\)达成一致, 为此, \(P_i\)首先发送\(u_i\)给所有服务器, 而这只需\(P_j\in\mathcal P\backslash P_i\)互相交换\(u_i\), 然后每个\(P_j\)从接收到的\(u_i\)的三个版本中选择最多的那个版本的\(u_i\)即可, 这由诚实大多数假设保证. 一旦协定完成, 每个服务器都将\(u_1,u_2,u_3,u_4\)中的占大多数的那个选为它们从用户接收到的值; 若没有任何一个出现占大多数, 那么就选择一个默认值.

    BA完成后, \(P_0\)从\(u\)中本地计算\(\beta_v+\gamma_v\), 同时\(P_1,P_2\)从\(u\)中本地计算\(\beta_v\). 对于\(v\)的重构, 服务器发送它们的\([\![v]\!]\)份额给用户, 用户选取每个份额中的占大多数的值重构输出. 在任何情况下, 如果协议识别出了TTP, 则所有服务器发送它们的份额给TTP, 由TTP选取每个份额中的占大多数的值计算功能函数的输出, 并把输出发给用户. 用户也从所有服务器中接收TTP的身份, 并接受来自占大多数的TTP的输出.

    Bit Extraction Protocol

    4PC下的比特抽取协议\(\Pi_\mathsf{bitext4}\): 为计算4PC下\([\![v]\!]\)的最高有效位的布尔分享\([\![\mathsf{msb}(v)]\!]^\mathsf B\), SWIFT仍使用了ABY3中优化的并行前缀加法器电路[Optimized Parallel Prefix Adder (PPA) circuit]方案. 因为\(v\)表示为\(v=\beta_v+(-\alpha_v)\), 因此该电路的两个输入分别为\(\beta_v, -\alpha_v\)的布尔分享\([\![\beta_v]\!]^\mathsf B,[\![-\alpha_v]\!]^\mathsf B\). \(P_1,P_2\)拥有\(\beta_v\), 可以通过\(\Pi_\mathsf{jsh4}\)协议生成\([\![\beta_v]\!]^\mathsf B\). 同理, \(P_0,P_3\)生成\([\![-\alpha_v]\!]^\mathsf B\). 于是通过优化的电路, 可计算出\([\![\mathsf{msb}(v)]\!]^\mathsf B\). 该协议预处理阶段的均摊通信量为\(7\ell-6\)比特, 在线阶段需要1轮, 均摊通信量为\(7\ell-6\)比特.

    Bit2A Protocol

    4PC下的布尔分享与算术分享转换协议\(\Pi_\mathsf{bit2A4}\), 与3PC下的相比, 4PC下的原理在于:

    设\(e=\alpha_b\oplus\gamma_b, c=\beta_b\oplus\gamma_b\), 则

    \[b^\mathsf R=(\alpha_b\oplus \beta_b)^\mathsf R=((\alpha_b\oplus\gamma_b)\oplus(\beta_b\oplus\gamma_b))^\mathsf R=(e\oplus c)^\mathsf R=e^\mathsf R+c^\mathsf R-2e^\mathsf Rc^\mathsf R. \]

    \(\Pi_\mathsf{bit2A4}\)的预处理阶段均摊通信量为\(3\ell+4\)比特, 在线阶段需要1轮, 均摊通信量为\(3\ell\)比特.

    image-20220105193218898

    Bit Injection Protocol

    比特映射协议\(\Pi_\mathsf{bitinj4}\): 给定比特\(b\)的布尔分享\([\![b]\!]^\mathsf B\)和\(v\in\mathbb Z_{2^\ell}\)的算术分享\([\![v]\!]\), 计算\([\![bv]\!]\).

    简单的方法是先把\([\![b]\!]^\mathsf B\)通过\(\Pi_\mathsf{bit2A4}\)转化为\([\![b]\!]\), 然后通过乘法协议\(\Pi_\mathsf{mul4}\)计算\([\![bv]\!]\). 下面介绍一种减少预处理阶段和在线阶段通信量的方法.

    记\(z=b^\mathsf Rv\), 注意到

    \[\begin{aligned} z&=b^\mathsf Rv=(\alpha_b\oplus\beta_b)^\mathsf R(\beta_v-\alpha_v)\\ &=((\alpha_b\oplus\gamma_b)\oplus(\beta_b\oplus\gamma_b))^\mathsf R((\beta_v+\gamma_v)-(\alpha_v+\gamma_v))\\ &=(c_b\oplus e_b)^\mathsf R(c_v-e_v)=(c_b^\mathsf R+e_b^\mathsf R-2c_b^\mathsf Re_b^\mathsf R)(c_v-e_v)\\ &=c_b^\mathsf Rc_v-c_b^\mathsf Re_v+(c_v-2c_b^\mathsf Rc_v)e_b^\mathsf R+(2c_b^\mathsf R-1)e_b^\mathsf Re_v. \end{aligned} \]

    其中, \(c_b=\beta_b\oplus\gamma_b, e_b=\alpha_b\oplus\gamma_b,c_v=\beta_v+\gamma_v,e_v=\alpha_v+\gamma_v\).

    具体协议如下图, 预处理阶段均摊通信量为\(6\ell+4\)比特, 在线阶段需要1轮, 均摊通信量为\(3\ell\)比特.

    image-20220105220329517

    Dot Product

    4PC下的点积协议\(\Pi_\mathsf{dotp4}\). 预处理阶段需要\(3\ell\)比特的均摊通信量, 在线阶段需要1轮, \(3\ell\)比特的均摊通信量.

    image-20220106094420778

    Truncation

    4PC下的截断对生成协议\(\Pi_\mathsf{trgen4}\). 在线阶段需要1轮, \(\ell\)比特的均摊通信量.

    image-20220106094541792

    Dot Product with Truncation

    4PC下的点积截断协议\(\Pi_\mathsf{dotpt4}\). 预处理阶段需要\(4\ell\)比特的均摊通信量, 在线阶段需要1轮, \(3\ell\)比特的均摊通信量.

    image-20220106094635955

    Activation Functions

    • ReLU函数计算: 预处理阶段均摊通信量为\(13\ell-2\)比特, 在线阶段需要\(\log\ell+1\)轮, 均摊通信量为\(10\ell-6\)比特.
    • Sigmoid函数: 预处理阶段均摊通信量为\(23\ell-1\)比特, 在线阶段需要\(\log\ell+2\)轮, 均摊通信量为\(20\ell-9\)比特.

    Experiment

    Logistic Regression

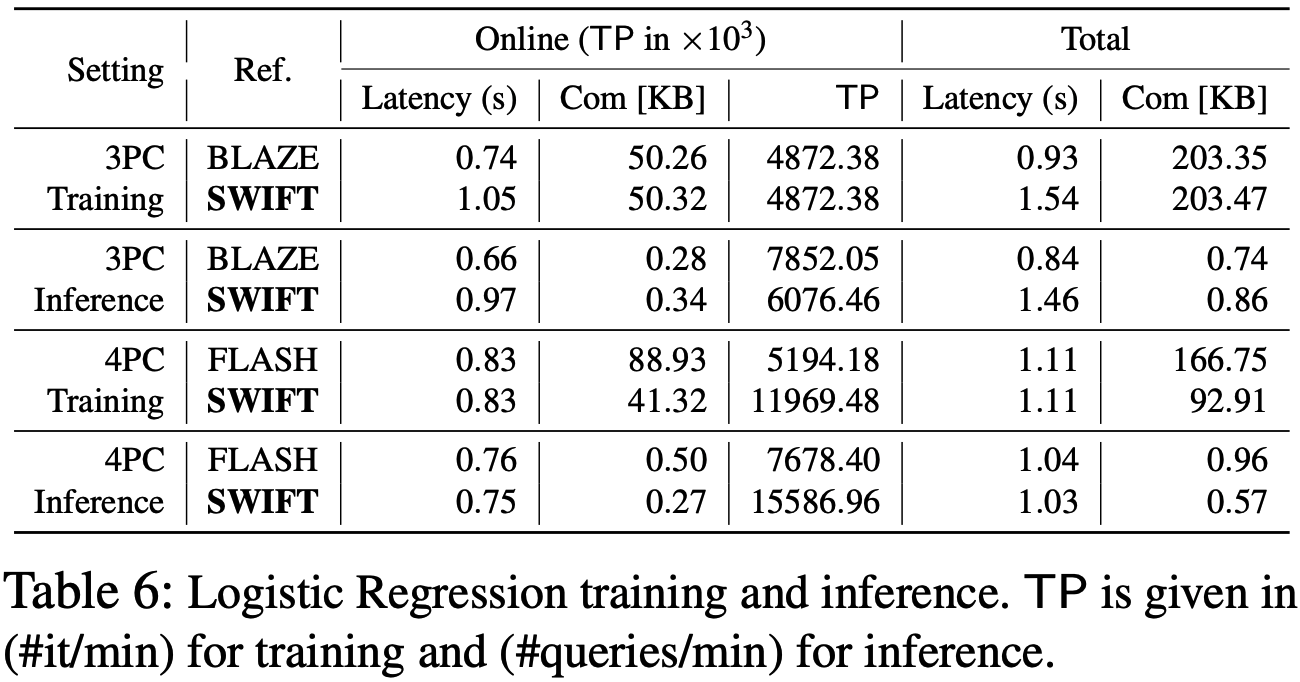
    image-20220106111858354

    NN Inference

    SWIFTT78

    Conclusion

    本文提出了一个高效PPML框架SWIFT, 实现了输出可达性(GOD)的更强安全需求，其中3PC协议基于BLAZE且实现GOD而无额外开销. 4PC协议基于实现GOD的FLASH和实现Fairness的Trident. SWIFT框架能实现GOD的关键在于文章所引入的Joint message passing原语，若发现信息不一致，则会选出一个必为诚实参与方的TTP进行明文计算. 而减少通信开销的关键仍在于试图让点积运算的开销最小化, 即使开销独立于向量长度.

    References

    [1] A. Patra and A. Suresh. BLAZE: Blazing Fast Privacy-Preserving Machine Learning. NDSS, 2020.

    [2] A. Dalskov, D. Escudero, and M. Keller. Fantastic Four: Honest-Majority Four-Party Secure Computation With Malicious Security. USENIX, 2021.

    [3] H. Chaudhari, R. Rachuri, and A. Suresh. Trident: Efficient 4PC Framework for Privacy Preserving Machine Learning. NDSS, 2020.

    [4] M. Byali, H. Chaudhari, A. Patra, and A. Suresh. FLASH: fast and robust framework for privacy-preserving machine learning. PETS, 2020.

    [5] B. Alon, E. Omri, and A. Paskin-Cherniavsky. MPC with Friends and Foes. CRYPTO, 2020.


    本文标题: SWIFT: Super-fast and Robust Privacy-Preserving Machine Learning
    本文作者: 云中雨雾
    本文链接: https://weiviming.github.io/16449265418549.html
    本站文章采用 知识共享署名4.0 国际许可协议进行许可
    除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
    最后编辑时间: 2022-02-15T20:02:21+08:00