Fantastic Four: Honest-Majority Four-Party Secure Computation with Malicious Security
今天给大家带来的是发表于USENIX Security'21的一篇文章Fantastic Four: Honest-Majority Four-Party Secure Computation with Malicious Security, 报告的slide见这里.
Abstract
本文介绍了一种诚实大多数的鲁棒四方计算协议, 具有主动安全性, 且不依赖于function-dependent preprocessing(预处理), 实现了输出可达性(Guaranteed output delivery, GOD), 同时保证协议中止同时确保任何一方不会得到超过输出的任何信息. 以往实现输出可达性采用的方案有SWIFT1, FLASH2, 让确定为诚实的参与方重构秘密并在明文下进行协议计算. 实验表明, 本文所提协议的效率接近于仅提供半诚实安全的三方诚实大多数计算协议, 这表明, 通过添加第四方是实现主动安全而不影响性能的有效方案.
Background
当前最快的MPC协议仅提供了中止安全性. 传统的MLaaS架构缺乏隐私保护, 而客户端/服务器模型(client/server model)是MLaaS架构常用的隐私保护替代方案, 如果存在恶意的计算方导致中止计算, 那么用户将无法得到输出, 这对于MLaaS来说是不能接受的, 因此模型的鲁棒性非常重要. 这里的鲁棒性可以理解为, 协议为所有参与方提供输出可达性, 而不论敌手是否存在恶意行为. 考虑MLaaS架构中的两种鲁棒类型的外包计算:
-
传统鲁棒(traditional robustness)外包计算: 保证计算最后一定输出正确的结果. 考虑具体场景: 假设\(P_1,P_2,P_3,P_4\)四方进行MLaaS隐私计算, 其中一方是腐化方, 且协议是鲁棒的. 假设某次计算中\(P_2\)发现\(P_1\)和\(P_4\)的输入不一致, 意味着\(P_1\)和\(P_4\)中的某一方是恶意的, \(P_2\)广播该消息, 虽然鲁棒性要求计算不能中止, 但是有一点是所有计算方都可以肯定的: \(P_3\)肯定是诚实的, 则鲁棒性很容易达到, 为此所有参与方将他们的分享发给\(P_3\)重构输入, 然后再明文计算即可, 因此, 很容易实现输出可达性. 但这在现实中通常是不合理的, 因为\(P_3\)掌握了用户的所有输入, 而用户更希望数据在计算时始终保持隐私性.
-
隐私鲁棒(private robustness)外包计算: 这种类型下的外包计算也可以保证计算最后输出正确的结果, 但不依赖于诚实方获得用户的隐私输入. 本文介绍了如何通过四方和三方协议之间的转换来达到这一点.
Main Contributions
- 提出了\(\mathbb{Z}_{2^k}\)上抵抗一个腐化方的主动安全的四方计算协议, 在相同设定下与当前好的方案整体复杂性相同, 除了常数开销的设定外, 无需任何预处理. 此外, 本文的方案允许丢弃后面计算中不必要的中间信息.
- 提出了\(\mathbb{Z}_{2^k}\)上抵抗一个腐化方的主动安全的三方计算协议, 虽然在线阶段的通信复杂度略高于当前最好的方案BLAZE3, 但总体复杂性低几个数量级, 主要原因是点积计算的通信量与输入的长度无关.
- 通过训练MNIST, 进行了协议的基准测试, 并进一步考虑了定点精度的参数选取对训练准确度的影响.
- 展示了如何在保持隐私性的同时使得四方协议具备鲁棒性.
本文的所有协议在MP-SPDZ中可用.
Secure Protocol
Replicated Secret Sharing
记四个参与方分别为\(P_i,P_j,P_g,P_h\), 其中\(i,j,g,h\in\{1,2,3,4\}\), 本文使用秘密共享方案是复制秘密共享(Replicated Secret Sharing). Dealer在四方下秘密共享秘密\(s\in\mathbb Z_{2^k}\)的方法(文章中的协议1), 如下图所示:
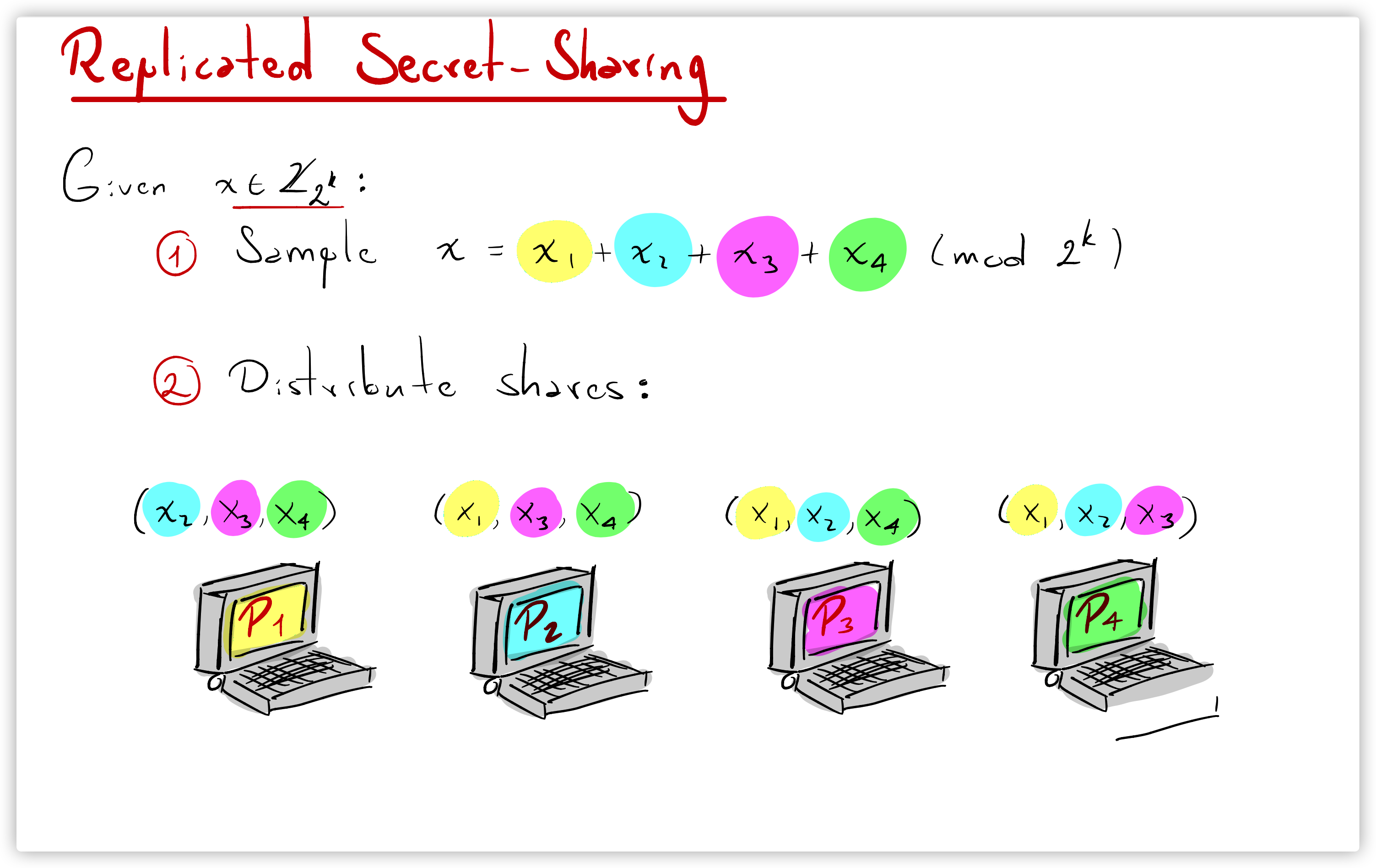
-
在\(\mathbb Z_{2^k}\)上选取三个随机数\(s_1,s_2,s_3\), 然后令\(s_4=s-(s_1+s_2+s_3)\);
-
发送\(\{s_j\}_{j\neq i}\)给\(P_i\), 记秘密共享为\([s]\).
这意味着每方各持有的三个秘密分享, 且任意两方都可以恢复秘密\(s\). 由于该方案是线性的, 因此秘密分享形式下的加法和数乘都是无需交互, 这里不再介绍.
Joint Message Passing

协议2用于当两方共有某个秘密需要发给第三方时, 进行的作弊识别检测. 假设\(x\)是\(P_i\)和\(P_j\)共有的信息, 需要发送给\(P_g\), 为此\(P_i\)发送\(x\), \(P_j\)发送\(H(x)\), 然后\(P_g\)检查从\(P_i\)收到的\(x\)的hash值是否与\(H(x)\)匹配, 若不匹配则发出中止信号\(err\)并指控\(P_i\)和\(P_j\), 参与方执行协议2, 输出最多两个参与方的集合, 其中一个参与方是恶意的.
JMP根据参与方的行为, 分为以下几种情况:
- 若\(P_h\)是恶意的, 则不会产生任何中止信号;
- 若\(P_g\)是恶意的, 则\(P_g\)将错误地指控\(P_i,P_j\), 按照协议, \(P_g\)将广播\(P_i,P_j,c_i,c_j\). 若\(c_i=c_j\), 则参与方直接输出\(\{P_g\}\). 否则, 由于\(P_i\)和\(P_j\)都是诚实的, 则\(P_g\)广播的信息中必然有一项与\(P_i,P_j\)发送给它的信息不符合, 因此这两方之中必然有一方会指控\(P_g\), 例如\(P_i\)发出了指控, 此时参与方只需输出\(\{P_j,P_g\}\)组成的集合. 不管哪种情况, 输出的集合中都必然包含恶意方\(P_g\);
- 若\(P_i\)是恶意的, \(P_i\)将发送错误的信息给\(P_g\), \(P_g\)作为诚实方发现从\(P_i\)和\(P_j\)收到的信息不一致, 将指控\(P_i\)和\(P_j\), 此时只有\(P_i\)会指控\(P_g\), 因为\(P_g\)正确地广播了\(P_j\)发送的值. 如果\(P_i\)指控了\(P_g\), 则参与方将\(\{P_i,P_g\}\)作为输出, 否则将\(\{P_i,P_j\}\)作为输出, 不管哪种情况都有\(P_i\)在集合中. \(P_j\)是恶意的情形与\(P_i\)类似.
由于JMP仅是三方协议, 因此文章假定没有参与JMP的计算方总是诚实的.
Shared Input
本节介绍秘密\(x\in\mathcal R\)如何在恶意安全下将\(x\)分享给各参与方, 使得各参与方获得\(x\)的份额\([x]\), 为此可以通过伪随机生成器\(\mathsf{PRG}\)来完成. 分两种情况:
- 若有三个参与方\(P_i,P_j,P_h\)知道\(x\), 则不需要交互即可完成对\(x\)的秘密分享: 令\(x_i=x_j=x_h=0,x_g=x\)即可, 记为\([x]\leftarrow\mathsf{INPLocal}(x,P_i,P_j,P_h)\).
- 若只有两个参与方知道\(x\), 则可以借助\(\mathsf{PRG}_k\)(伪随机生成器)来完成, 其中\(k\)是密钥. 具体方案如下图协议3. 这里的第3步需要调用JMP确保\(P_g\)获得的\(x_h\)与\(P_i, P_j\)计算得到的是一致的.

Secure Multiplication
为计算\(x,y\)秘密分享的乘法\(xy\), 为此, 按照秘密共享形式将\(xy\) 展开, 我们得到如下几项, 乘法的目标就是计算所有这些项的和. 其中\(x_iy_i\)这一类的项是参与方无需交互就能计算的, 因为只有\(P_i\)无法计算这一项, 为此令\(P_i\)的三个分享都为0, 其他参与方的其中一个分享为\(x_iy_i\), 其余为0即可. 因此关键在于计算交叉项之和(文章的协议3).

下面以\(z:=x_1y_2+y_1x_2\)为例, 这一项\(P_3,P_4\)可以本地计算得到, 问题转化为\(P_3, P_4\)已知秘密\(z\), 如何向\(P_1,P_2\)秘密分享\(z\), 为此可以借助\(\mathsf{PRG}_k\)(伪随机生成器), \(k\)是密钥. 假设\(P_2,P_3,P_4\)之间有预分享的密钥\(k\), 首先\(P_2,P_3,P_4\)计算随机数\(z_1=r=\mathsf{PRG}_k()\)作为其中一个分享, \(P_3,P_4\)设定另一个分享为\(z_2=z-r\), 然后\(P_1,P_2\)令\(z_3=z_4=0\), 接下来只需让\(P_3\)发送\(z_2\)给\(P_1\)即可完成交叉项秘密分享. 由于是恶意安全模型下, 需要确保参与方\(P_3\)发送给\(P_1\)的信息和\(P_4\)持有的都是\(z_2\), 为此需要进行三方作弊识别检测(文章的协议2, Joint Message Passing), 并使得\(P_1\)得到正确的\(z_2\). 其余交叉项情况类似, 因为一共有6个这样的交叉项求和, 因此, 计算一个秘密分享的乘法算子需要发送6个元素, 整个乘法算子的计算步骤见文章协议4. 文章指出, 本文的方案除了JMP部分的哈希函数和伪随机生成器的状态之外, 不需要保留任何后续计算不再需要的秘密分享, 不依赖于功能函数的预处理阶段.
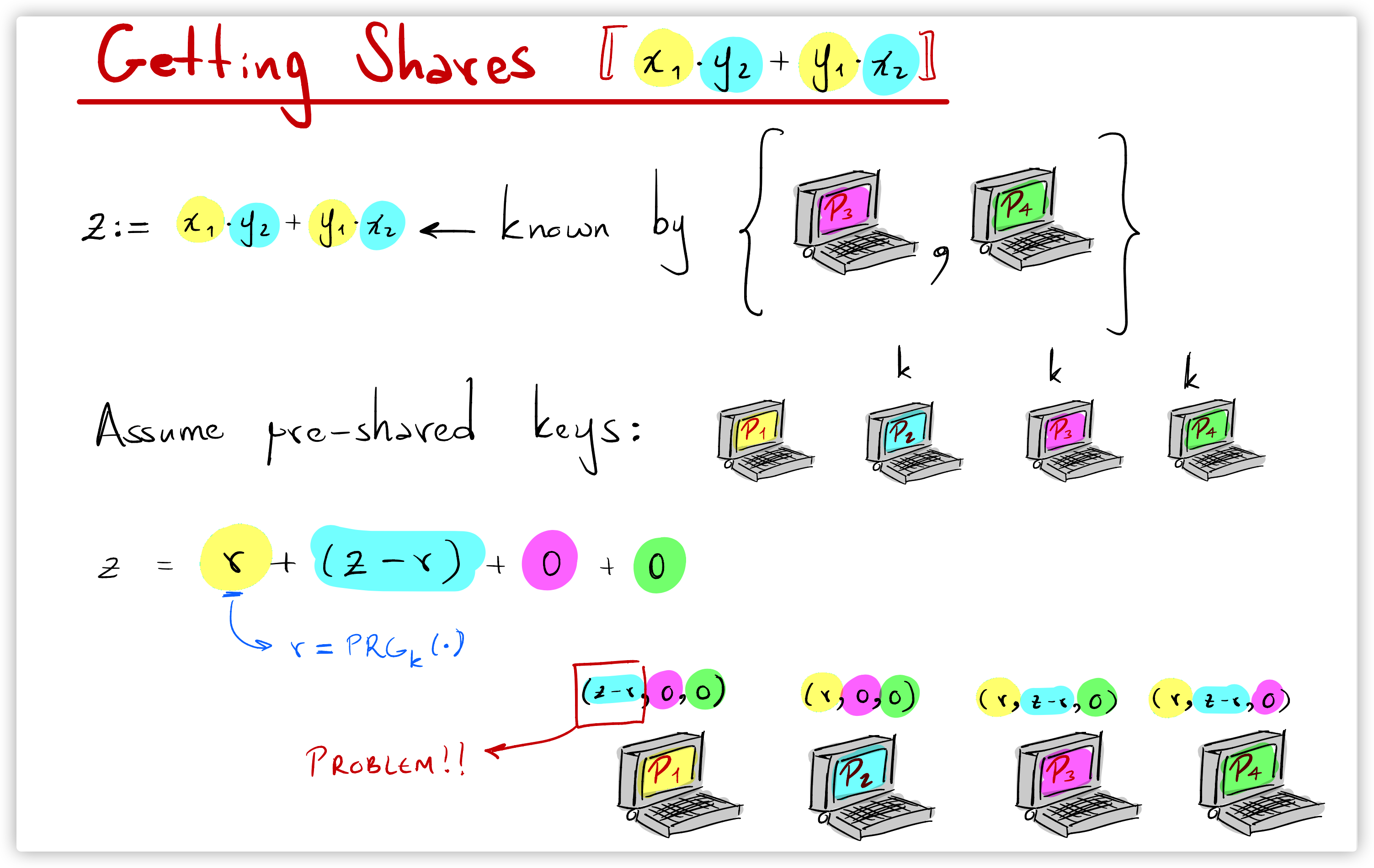

Probabilistic Truncation

为了处理多方计算的定点算术(fixed-point arithmetic)问题, 本文将Dalskov等人4与SWIFT1的截断协议相结合给出概率截断的MPC协议(协议5).
给定\(\mathbb Z_{2^k}\)上的秘密份额\([x]\)和定点精度\(m\), 截断协议的目标是获得份额\([y]\), 这里的\(y=\lfloor x/2^m\rfloor\), 这等价于获得\(y=\lfloor x/2^m\rceil\). 在概率截断中, 我们更关注\(\lfloor x/2^m\rceil\)的最佳近似(就近取整). 具体而言, \(y=\lfloor x/2^m\rceil+u\), 其中\(u\in\{0,1\}\)更偏向于正确结果\(\lfloor x/2^m\rceil\), 即若\(x/2^m\)更接近于\(\lceil x/2^m\rceil\), 则\(u=1\); 若\(x/2^m\)更接近于\(\lfloor x/2^m\rfloor\), 则\(u=0\). 换而言之, \(u=1\)的概率为\((x\bmod 2^m)/2^m\). 举个例子, 若\(x=7,m=2\), 此时正确的结果应为\(7/2^2=1.75\), 概率截断协议给出的可能结果为\(\lfloor 7/4\rfloor=1\), 或\(\lfloor7/4\rfloor+1=2\), 后者即\(u=1\)的概率为\((7\bmod 2^2)/2^2=0.75\), 刚好是正确结果的小数部分.
为说明协议5的正确性, 令\(x\)是正数, 即\(\mathsf{MSB}(x)=0\), 则有\(0<x<2^{k-1}, x\bmod2^{k-1}=x\), 这意味着我们有: \(c=x+r\bmod2^k\), 这等价于\(c=x+r-2^ku\), 其中\(u\)是溢出标识比特, 即\(u=(x+r\geq _?2^k)\). 另一方面, 我们有\(c\bmod2^{k-1}=x\bmod2^{k-1}+r\bmod2^{k-1}\), 这等价于\(c\bmod 2^{k-1}=x\bmod2^{k-1}+r\bmod2^{k-1}-2^{k-1}b\), 其中\(b=(x\bmod2^{k-1}+r\bmod2^{k-1}\geq_?2^{k-1})\). 若记\(r_{k-1}=\mathsf{MSB}(r)\), 则可以证明\(u=b\cdot r_{k-1}\).
根据带余除法, 有\(r=2^{k-1}\cdot r_{k-1}+(r\bmod2^{k-1})\), \(c=2^{k-1}\cdot \lfloor c/2^{k-1}\rfloor+(c\bmod2^{k-1})\), 记\(c''=\lfloor c/2^{k-1}\rfloor\), 利用性质: 若\(a,b\)是两个比特, 则有\(a\oplus b=a+b-2ab\). 我们有
\[\begin{aligned} 2^{k-1}\cdot c''&=c-(c\bmod2^{k-1})\\ &=(x+r-2^ku)-(x+(r\bmod2^{k-1})-2^{k-1}b)\\ &=2^{k-1}r_{k-1}+2^{k-1}b-2^k\cdot b\cdot r_{k-1}\\ &=2^{k-1}(r_{k-1}+b-2br_{k-1})\\ &=2^{k-1}(r_{k-1}\oplus b). \end{aligned} \]故有\(c''=r_{k-1}\oplus b\), 于是\(b=c''\oplus r_{k-1}\).
因为\(x\bmod2^{k-1}=x\), 则有\((c\bmod2^{k-1})=x+(r\bmod2^{k-1})-2^{k-1}b\), 两边除于\(2^m\)并下取整得
\[c'=\lfloor\frac{(c\bmod2^{k-1})}{2^m}\rfloor=\lfloor\dfrac{x+(r\bmod2^{k-1})}{2^m}\rfloor-2^{k-m-1}b, \]其中
\[\lfloor\dfrac{x+(r\bmod2^{k-1})}{2^m}\rfloor=\lfloor \dfrac{x}{2^m}\rfloor+\lfloor\dfrac{(r\bmod2^{k-1})}{2^m}\rfloor+w, ~~~~w\in\{0,1\}. \]而\(r'=\lfloor\dfrac{(r\bmod2^{k-1})}{2^m}\rfloor\), 于是协议5的第7步输出为
\[c'-r'+2^{k-m-1}b=\lfloor \dfrac{x}{2^m}\rfloor+w. \]因此, \(w=1\)的概率等于\(\dfrac{x}{2^m}\)的小数部分, 即概率截断输出更倾向于\(\lfloor \dfrac{x}{2^m}\rceil\).
Random Bit Generation for 4PC
生成随机比特是多方计算中一个基础原语. 协议6给出了4PC下的具体方案, 总体思想是将参与方分为两组, 每组通过预分享的密钥生成随机比特, 然后再对其进行秘密分享, 通过比特运算与算术运算的关系来生成随机比特\(b\). 因为每组中至少有一个参与方是诚实的, 所以恶参与方可以在INP协议中检测出来, 因此可以保证\(b\)的正确性.

Mix-Circuit Computation
比较和截断等非线性函数的计算通常在二进制计算(Binary computation)中更高效, 这反过来要求在算术运算(Arithmetic computation)和二进制运算中相互转换, 因为算术运算明显快于点积运算. 有两种方法来实现转换:
- 对于某些秘密共享方案, 可以使用SPDZ, ABY, ABY3的B2A/A2B协议.
- 使用Rotaru和Wood的double-authenticated bits(daBits)方案, 在两个计算域中共享随机比特份额, 这些随机比特可以盲化(mask)秘密值. 例如, 若\(x\)是计算中的一个比特, \(r\)是秘密随机比特, 在计算域中打开\(x\oplus r\)不会泄漏任何信息, 于是可以在另一个计算域中计算\(x=(x\oplus r)\oplus r\), 因为\(r\)在两个计算域中是通过构造来获得. 由于\(r\)的生成与秘密无关, 因此非常适合于offline-online范式的多方计算协议中.
Escudero等人5将第二种方法从1比特扩展到了\(m\)比特, 提出了extended daBits(edaBits), 并介绍了如何在任意安全模型中生成edaBits. 本文提出了在复制秘密共享模数为二次幂的高效生成预处理edaBits的方案. 构造的关键在于将生成edaBits中的使用的溢出校正(overflow correction)与复制秘密共享的本地份额转换相结合, 文章称之为份额拆分(Share splitting). 具体方案如下图协议7, 其中\(x[j]\)表示\(x\)的第\(j\)比特. 协议7可以扩展到\(n\)方复制秘密共享中.
协议8给出了高效生成edaBits的方法. edaBits是由\(\mathbb Z_{2^k}\)上秘密分享的随机值\([r]_{2^k}\)和它比特\(\{r[i]\}_{i=0}^{k-1}\)的二进制分享\([r]_2\)组成的对\(([r]_{2^k},[r]_2)\).若\(r\in\{0,1\}\)是均匀随机的, 则edaBits即为daBits. 通过daBits可以将\([b]_{2}\)转换为\([b]_{2^k}\): 参与方打开\(c\leftarrow[r]_2+[b]_2\), 然后计算\([b]_{2^k}=[r]_{2^k}+c-2\cdot c\cdot [r]_{2^k}\). 根据这个假设, 可以扩展生成\(m\)比特的edaBits.

3PC with Malicious Security

本文实现鲁棒性依赖于三方计算. 与SPDZ类似, Abspoel等人的方案通过加入MAC到秘密份额中使得作弊可以被检测出来, 但他们的方案不支持连续计算, 因为它涉及验证正确性的最后检测阶段, 在此之前的一切都不被信任, 由于检测会泄漏某些防止作弊的秘密信息, 检测后无法进一步计算. 本文通过修改他们的验证协议, 通过献祭(sacrificing)在底层协议中的一个额外的秘密乘法, 使得这些秘密信息被隐藏起来, 以利于连续计算. 连续计算的好处是允许将秘密共享信息保存更长时间. 在实际操作方面, 检测协议将每个乘法的信息保留到检测阶段. 此外, 连续计算可以减少存储要求, 因为它允许定期检查, 从而删除中间信息.
设\(\langle x\rangle=([x]_{2^{k+s}},[r\cdot x]_{2^{k+s}})\)是\(x\)的SPDZ份额, 其中\(r\in\mathbb{Z}_{2^s}\)是全局MAC密钥. 见协议9, 这里直接使用了基于RSS的在模数为二次幂上的Zero-check功能函数\(\mathcal F_\mathsf{CheckZero}\). 这里简单介绍一下协议9中的Zero-check的具体思路6, 设存在一个随机预言机\(\mathcal H\), 若\(\sum_{i}x_i=0\), 则\(x_{i-1}\equiv_{k+s} -(x_i+x_{i+1})\), 因此\(P_i\)发送\(z_i=\mathcal H(-(x_i+x_{i+1}))\)给\(P_{i+1}\), 而\(P_{i+1}\)和\(P_{i-1}\)都有\(x_{i-1}\), 因此\(P_{i+1}\)可以检测\(z_i=\mathcal H(x_{i-1})\)是否成立, 若不成立, 则直接输出中止(Abort).
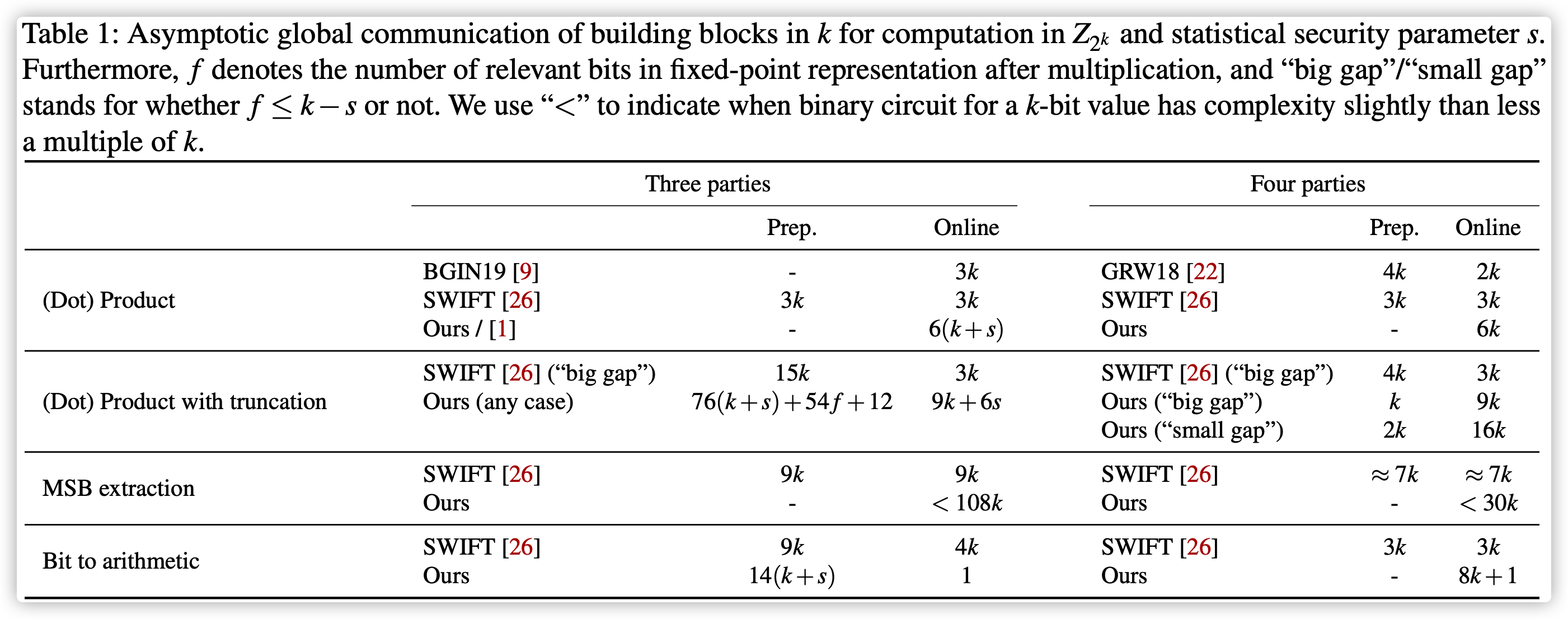
复杂度: 协议9底层协议中, 每个点积计算参与方需要发送\(k+s\)比特, 每个输入输入方需要发送\(2(k+s)\)比特. 因此在协议9中, 所有参与方的点积开销为\(6(k+s)\), 输入开销为\(3(k+s)\). 因此, 点积的开销与向量长度\(n\)无关.
Random Bit Generation for 2PC

这里考虑的是2PC的情况, 与上面的有所区别.
生成具有半诚实安全性的随机比特的方法是两个不同参与方输入随机比特, 然后计算XOR即可.
然而在恶意安全的情况下, 恶意参与方可能输入的\(b\)可能不是一个比特, 为此在不泄漏\(b\)的前提下, 可以通过计算\(b(1-b)=0\)是否成立来检测是否有\(b\in\{0,1\}\). 本文构造的随机比特生成协议也使用了这一原理, 见协议10. 如果\(b_i=0\), 则最后一步检测将成功. 不失一般性, 假设\(P_0\)是诚实的, 因为
\[b_i=b_i^0\oplus b_i^1=b_i^0+b_i^1-2\cdot b_i^0\cdot b_i^1= \begin{cases} b_i^1, & b_i^0=0 \\ 1-b_i^1, & b_i^0=1. \end{cases} \]即, 无关\(b_i^0\), \(b_i\in\{0,1\}\)当且仅当\(b_i^1\in\{0,1\}\). 这种方法排除了对\(b_i^0\)的选择失败攻击.
Communication Cost
本文的三方协议比其他工作慢一个数量级, 四方相差大约2倍.
Privacy Robustness
Slide的这个图很容易理解文章隐私鲁棒性的实现思想, 现在来说明总体的转换思路, 参与方之间约定若JMP输出了恶意参与方的集合, 则优先将索引数小的那个参与方是恶意参与方, 排除该参与方再进行后续计算. 继续背景中的场景, 因为\(P_1\)和\(P_4\)其中必有一方是恶意的, 先假设\(P_1\)是恶意的, 即排除\(P_1\), 剩下的三方将输入的四方秘密分享转化为三方秘密分享, 然后使用中止安全(Security with abort)的三方协议进行隐私计算. 如果在计算中仍然出现了中止信号, 说明\(P_4\)是恶意的, 排除\(P_4\), 剩下的\(P_2,P_3\)使用被动安全的两方计算协议完成隐私计算, 此时可以引入诚实的\(P_1\)生成乘法三元组协助两方进行隐私计算. 这样既可以在不向计算方泄漏用户的隐私信息的前提下完成计算, 又提供了鲁棒性, 达到了预期目标. 文章的JMP协议给出了当出现中止信号时, 检测恶意参与方的方法.
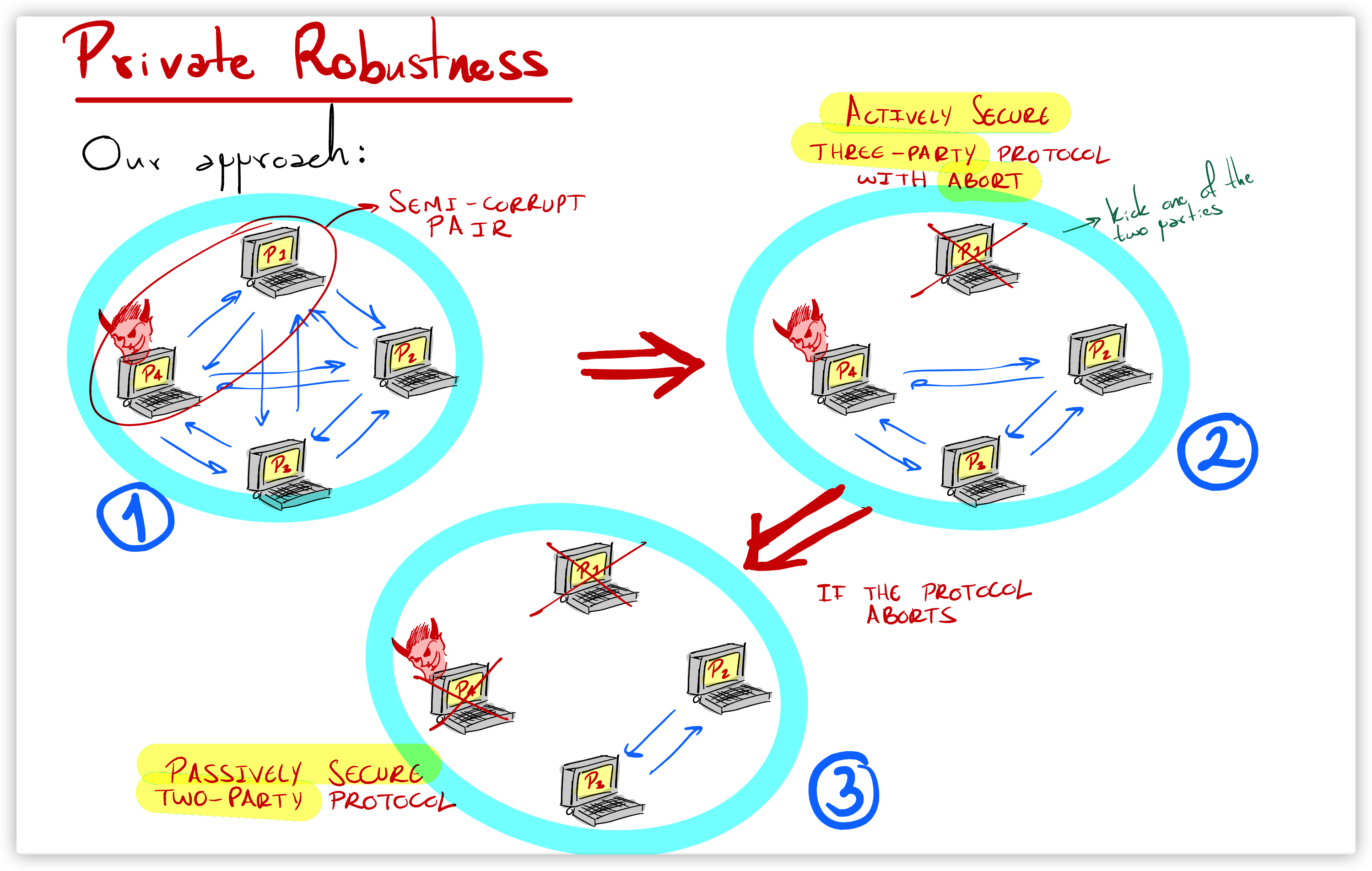
现在说明排除潜在的恶意参与方后, 如何实现份额转换.
设\(x=x_1+x_2+x_3+x_4\), 参与方\(P_i\)拥有的份额为\(\{x_j\}_{j\neq i}\).
- 四方份额转三方份额: 假设\(P_1\)被排除, 则进行如下转换: \(P_2,P_3\)定义\(x'=x_1+x_4\), \(P_4\)丢弃\(x_1\). 这样, \(P_2\)的持有的份额为\((x',x_3)\), \(P_3\)持有的份额为\((x_2,x')\), \(P_4\)的持有份额为\((x_2,x_3)\). 此后计算为恶意安全的三方计算.
- 三方份额转两方份额: 假设\(P_4\)被排除, 则进行如下转换: \(P_2\)定义\(x''=x'+x_3\), \(P_3\)丢弃\(x'\). 这样, \(P_2\)的持有份额为\(x''\), \(P_3\)的持有份额为\(x_2\). 此后计算为半诚实安全的两方计算, 但可以引入诚实方生成乘法三元组协助两方进行计算.
Experiment
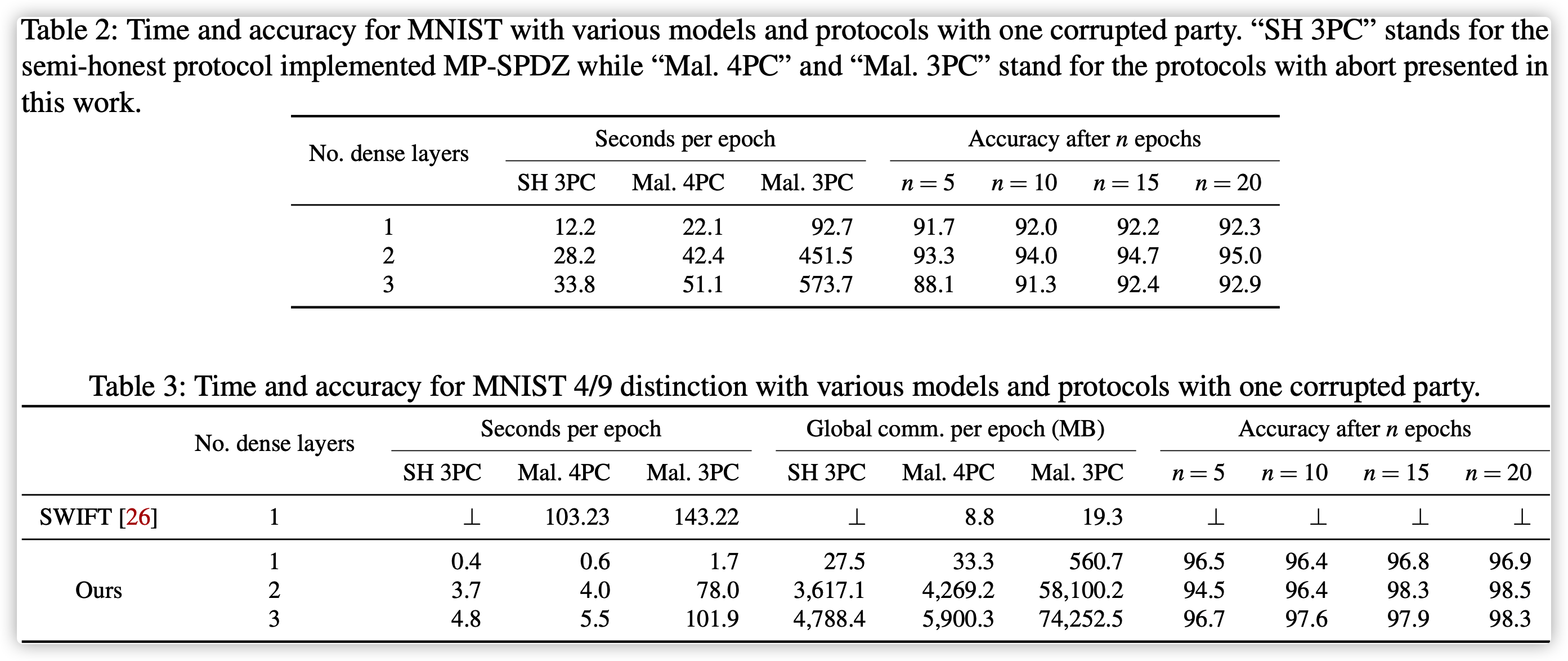
文章中的实验仅实现了中止安全性. 表2展示了不同安全模型下3层网络训练MNIST的计算开销和不同epoch下的模型准确率. 此外, 表3中可以看出文章所提出的半诚实安全的3PC和恶意安全的4PC开销基本相近.
The Impact of Fixed-Point Precision
MPC使用浮点算术(float-point arithmetic)通常可以获得更好的准确性, 但开销也相对较大, 因此通常MPC使用的是效率更高的定点算术(fixed-point arithmetic). 但定点算术的方法由于需要进行概率截断, 可能会导致模型的准确率下降, 先前的工作所选的参数在小型模型上具有较好的准确率, 但大多忽略了在大型模型中的准确性降低的程度. 文章分别对比了不同定点精度与计算域位长导致的准确率和效率之间差异. 结果见表5和表6.
先前的工作大多要求概率截断中的精度比计算域最大长度\(k\)小得多, 误差概率为\(2^{\ell-k}\), 其中\(\ell\)是概率截断输入的长度. 表5表明这个概率大概为\(2^{-20}\). 为训练双层模型, 通常需要将每个数的误差概率限制为\(2^{-40}\).
表6说明虽然低精度截断使得通信量节省了大约1/3, 但较大的模数使得双层模型训练的时间增加了1倍.
此外, 文章还指出64比特模数和13比特定点精度不能满足大型模型训练要求, 表5双层模型定点精度为12时, 随着epoch增大, 模型的准确度反而下降.

Conclusion
SWIFT中不考虑对诚实方保护输入的隐私性, 为此本文提出了Privacy robustness, 在不泄漏任何参与方输入隐私的前提下, 实现了输出可达性. 提出的协议不需要预处理阶段, 但安全性保证的前提是假设诚实方只存储预期信息, 即协议执行完后诚实方不能恢复隐私输入, 为此本文设计的协议不含让诚实参与方恢复信息的步骤. 如果诚实方长期存储所有的输入信息, 则本文提出的方案不适用, 安全性假设较强.
References
-
Nishat Koti, Mahak Pancholi, Arpita Patra, and Ajith Suresh. Swift: Super-fast and robust privacy-preserving machine learning. Cryptology ePrint Archive, Report 2020/592, 2020. ↩ ↩2
-
Byali, Megha et al. “FLASH: Fast and Robust Framework for Privacy-preserving Machine Learning.” Proceedings on Privacy Enhancing Technologies 2020 (2019): 459 - 480. ↩
-
Arpita Patra and Ajith Suresh. BLAZE: Blazing fast privacy-preserving machine learning. In NDSS 2020. The Internet Society, February 2020. ↩
-
Anders P. K. Dalskov, Daniel Escudero, and Marcel Keller. Secure evaluation of quantized neural networks. PoPETs, 2020(4):355–375, October 2020. ↩
-
Escudero, D., Ghosh, S., Keller, M., Rachuri, R. & Scholl, P. Improved Primitives for MPC over Mixed Arithmetic-Binary Circuits. CRYPTO 2020. ↩
-
Mark Abspoel, Anders Dalskov, Daniel Escudero, and Ariel Nof. An efficient passive-to-active compiler for honest-majority MPC over rings. Cryptology ePrint Archive, Report 2019/1298, 2019. ↩
本文标题: Fantastic Four: Honest-Majority Four-Party Secure Computation with Malicious Security
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16337773581295.html
本站文章采用 知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间: 2021-10-09T19:02:38+08:00