不经意传输及其优化方案

本文整理了美国俄勒冈州立大学电子工程和计算机科学学院副教授Mike Rosulek关于安全多方计算与混淆电路的演讲主题的主要内容, 文中图片均来源于Mike Rosulek的演讲报告幻灯片. 整理如有错误之处, 恳请批评指正, 谢谢!

不经意传输(Oblivious Transfer, OT)是MPC的一种特殊情况, 有两个参与者Sender($S$, Alice)和Receiver($R$, Bob), $S$有两个秘密信息$m_0,m_1$, $R$有一个秘密的选择比特$c$, 不经意传输协议将使得$R$根据$c$的取值获得信息$m_c$, 但对$m_{1-c}$一无所知, 同时$S$由于不知$c$的具体取值, 因而对$R$具体获得的是$m_0$还是$m_1$一无所知. 不经意传输协议的一个重要应用是在混淆电路中用于传输Evaluator的输入所对应的标签值, 此外不经意传输在其他MPC协议中也有很重要的应用. 在混淆电路中使用的是对称加密运算, 因而是非常快速且廉价的(cheap), 但不经意传输中需要使用大量的公钥加密运算, 因此计算是非常昂贵(Inherently expensive)的. Impagliazzo和Rudich指出仅使用对称加密原语来构造不经意传输协议是不可能的¹. 下面将主要介绍不经意传输协议的一些优化方案.

一个标准的OT协议是一个确定性的功能函数, 输入信息都是由参与方给定的. 一个随机OT(Random OT, ROT)协议是一个随机化的功能函数, $m_0,m_1,c$都是协议均匀随机生成而非参与方给定的. Beaver去随机化定理²告诉我们, ROT可以很容易地转化为标准OT. 如果我们需要大量的标准OT, 可以通过离线/在线阶段来生成. 首先在离线预计算阶段中生成大量的ROT, 然后在在线阶段中使用Beaver去随机化技巧将ROT转化为确定性的标准OT. 下面我们将介绍Beaver在线阶段的转换方法.

Beaver去随机化方案

如下图所示, 设预计算阶段的ROT协议使发送方Alice获得两个随机信息$m_0^r, m_1^r$, 接收方Bob获得$c^r, m_{c^{r}}^r$, 这里的上标$r$与图中的美元符号含义相同, 设在线阶段Alice的需要发送的信息为$m_0,m_1$, Bob的选择比特为$c$. Beaver去随机化的主要思想是Alice使用ROT的两个随机信息$m_0^r, m_1^r$作为一次一密(OTP)来加密需要他发送的信息$m_0,m_1$, 并将盲化结果$(x_0,x_1)$发给Bob. 如果$c=c^r$, Alice发送的两个信息是$x_0=m_0^r\oplus m_0, x_1=m_1^r\oplus m_1$, Bob本地计算$x_c\oplus m_{c^r}^r=x_c\oplus m_c^r=m_c$即可得到选择比特$c$对应的秘密$m_c$, 但无法获得$m_{1-c}$. 但如果$c\neq c^r$, 按照上述步骤我们会发现Bob将无法获得正确的信息, 除非Alice交换$m_0^r, m_1^r$来加密$m_0,m_1$.

于是很自然地解决办法是, 我们可以让Bob告诉Alice是否有$c=c^r$, 为此, Bob向Alice发送$d=c\oplus c^r$, 然后Alice计算$x_0=m_d^r\oplus m_0,x_1=m_{1\oplus d}^r\oplus m_1$, 并发送$x_0,x_1$给Bob, Bob计算$x_c\oplus m_{c^r}^r=x_c\oplus m_{c\oplus d}^r=m_c$. 正确性容易验证, 若$d=0$, 说明$c=c^r$, Alice使用$m_0^r$来加密$m_0$, $m_1^r$来加密$m_1$; 若$d=1$, 说明$c\neq c^r$, Alice使用$m_0^r$来加密$m_1$, $m_1^r$来加密$m_0$. 容易看出, Bob这样做是安全的, 因为Alice从$d$中无法获知$c^r$的具体信息.

离线阶段的ROT的开销仍然是昂贵的, 但在线阶段由于只有简单的XOR运算, 因此非常快速. 需要特别注意的一点是, 一个ROT实例只能生成一个标准OT实例, 这是因为在线阶段中我们将ROT的输出作为一次一密的密钥来加密参与方所发送的消息, 因此一个ROT只能使用一次.

OT扩展

我们先从公钥加密(PKE)说起, 由于公钥加密的开销比对称加密(SKE)的开销大, 因此我们通常通过同时使用PKE和SKE的混合加密来最小化PKE的开销: 首先使用昂贵的PKE加密短密钥$s$, 然后使用使用$s$通过廉价的SKE来加密长信息$M$. 于是, 通过$\lambda$比特的PKE和廉价的SKE, 我们实现了$N$比特的PKE, 其中$\lambda$代表计算安全参数. 那么, 有没有类似于混合加密的方法, 仅通过$\lambda$次OT实例和廉价的SKE来得到大量的OT实例呢? 这就是OT扩展的出发点.

Beaver在1996年提出了OT扩展(OT extension)³. Beaver注意到Yao协议需要的OT数量正比于函数的输入的长度, 我们可以使用混淆电路来构造这样一个OT扩展协议: Alice和Bob分别输入长度为$\lambda$比特的$s_A$和$s_B$, 使用$s_A\oplus s_B$作为伪随机种子: (1) 生成$2n$个随机串, 组成$n$对随机消息$(m_{1,0},m_{1,1}),\cdots,(m_{n,0},m_{n,1})$; (2) 选取一个$n$比特串$r$; 最终Alice得到所有随机消息对$\{m_{i,b}\}_{i,b}$, Bob得到$r$以及$r$的第$i$比特$r_i$所对应的消息$\{m_{i,r_i}\}_i$, 其中$i\in\{1,\cdots,n\}$, 这里的$n\gg \lambda$.

通过这种方式生成的ROT实例数为$n$, 而实际使用的ROT实例数仅为$\lambda$, 通常将这部分实际使用的OT实例称为Base OT. 虽然Beaver的OT扩展协议并不实用, 因为需要使用Yao协议对包含大量PRG的布尔电路求值, 但它告诉我们OT扩展的想法是切实可行的.

IKNP协议: 半诚实安全的OT扩展协议

2003年的美密会Yuval Ishai, Joe Kilian, Kobbi Nissim, Erez Petrank共同发表了“Extending Oblivious Transfers Efficiently”, 即著名的IKNP协议⁴, 其原理主要是基于矩阵变换, IKNP协议标志着OT扩展逐渐走向实用.

协议描述

假设Alice和Bob想生成$n$个OT, Bob拥有一个长为$m$的选择比特串$r$, 这里$r$的每个比特都是每次OT的一个选择比特. Bob将$r$的比特分解排成一列向量, 然后将向量的每个元素重复并按行扩充成一个$n\times\lambda$维0-1矩阵$R$, 该矩阵每行的元素要么全为0, 要么全为1. Bob对该矩阵进行秘密共享, 生成两个秘密份额矩阵$(T,T')$, 若原始矩阵的行向量全为0, 则$T,T'$在该行的元素相同, 反之则不相同(如图中橙色部分表示原始矩阵行向量全为1的秘密份额). Alice随机生成一个长为$\lambda$的比特串$s$. 然后双方交换身份执行$\lambda$次Base OT(次数取决于矩阵的列数), 对于第$i$次Base OT, Bob将秘密份额矩阵的第$i$列元素$(T_i,T'_i)$作为Base OT发送方的输入信息, Alice将$s$的第$i$个比特$s_i$作为Base OT接收方输入的选择比特, 若$s_i=0$, 则Alice获得$T_i$(即右侧后面那个矩阵的第$i$列), 反之则Alice获得$T'_i$(即右侧前面那个矩阵的第$i$列). 运行$\lambda$次之后, Alice获得矩阵$Q$. 易见, 当$r$的某一位置上的选择比特为0时, Alice所得矩阵$Q$的行向量$q_i$与Bob秘密份额矩阵在该位置的所对应的行向量$t_i$相等, 而当$r$的某一位置上的选择比特为1时, Alice所得矩阵$Q$在该位置所对应行的行向量$q_i$等于Bob秘密份额矩阵在该位置的所对应行的行向量$t_i$异或上$s$. 即

$$q_i=\begin{cases} t_i,& \text{若} r_i=0\\t_i\oplus s, & \text{若} r_i=1 \end{cases}$$

其中$r_i$是$R$的第$i$行. 上式也可以统一写成如下形式:

$$q_i=t_i\oplus r_i\wedge s, \tag{1}$$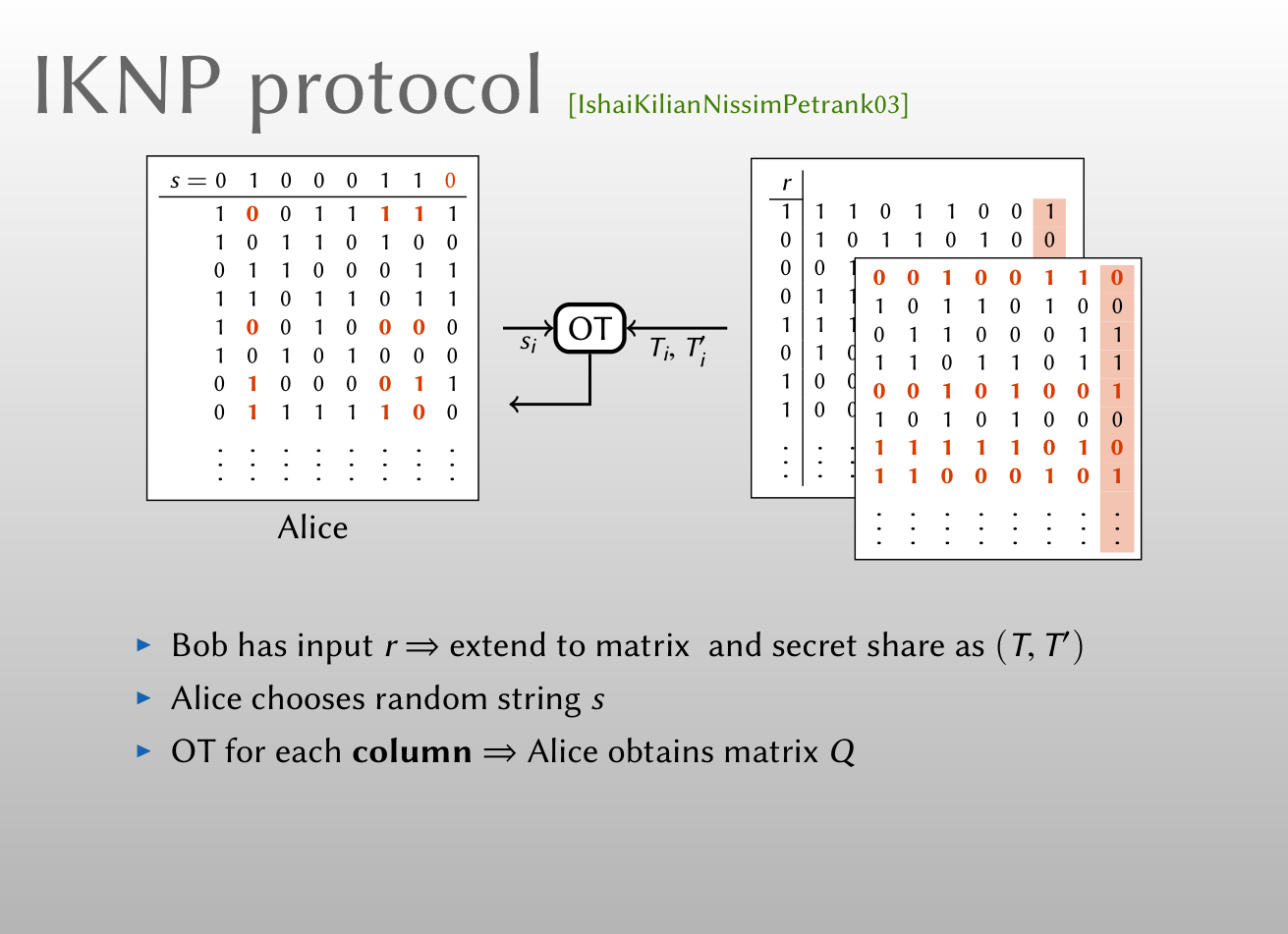

我们可以将上述过程抽象成下图的形式: 对于每个$i$, Bob得到$t_i$, Alice可以计算$q_i$和$q_i\oplus s$. 根据(1)式的关系, 我们可以将Alice所计算的的$q_i$和$q_i\oplus s$, 根据$r_i$的不同, 表示成下图中$t_i$与$s$关系的形式, 这可以看成是OT扩展中Alice作为发送者所拥有的秘密信息, 而从Bob的视角来看, 他所拥有的$t_i$刚好是Alice秘密信息中的其中一个!

但是, 对于Alice表格的每一行来说, 由于重用$s$, 导致了关联性. 为此, Alice和Bob可以采用一个随机预言机$H$来破坏这种关联性即可. IKNP协议的文章中指出, 实际上不需要更强的RO模型假设, 只需要假设$H$是一个关联健壮哈希函数(Correlation Robust Hash Function, CRHF)即可. 给定$t_1,\cdots,t_n$和秘密$s$, $H(t_1\oplus s),\cdots,H(t_n\oplus s)$是独立(伪)随机的, 通常称该性质为关联健壮性(Correlation Robustness), 而满足这种性质的哈希函数称为关联健壮哈希函数. 以上便是完整的IKNP协议的全过程.

如果从更高的视角来看IKNP协议, 可以想象一下我们有一个$n\times \lambda$维的高瘦矩阵, 其中$n\gg \lambda$. 我们通过对矩阵的每列进行$\lambda$次Base OT实例, 每次传输一个$n$比特长的串,通过逐行计算$H$来扩展随机OT实例. 很容易通过Beaver Derandomization Theorem将该随机OT扩展转换为标准OT扩展, 这里不做过多说明.

协议的安全性

安全性方面, IKNP协议是半诚实安全的. 具体而言, Alice可以是恶意的, 但Bob只能是半诚实的, 下面将介绍如果Bob是恶意的, IKNP协议会存在的问题.

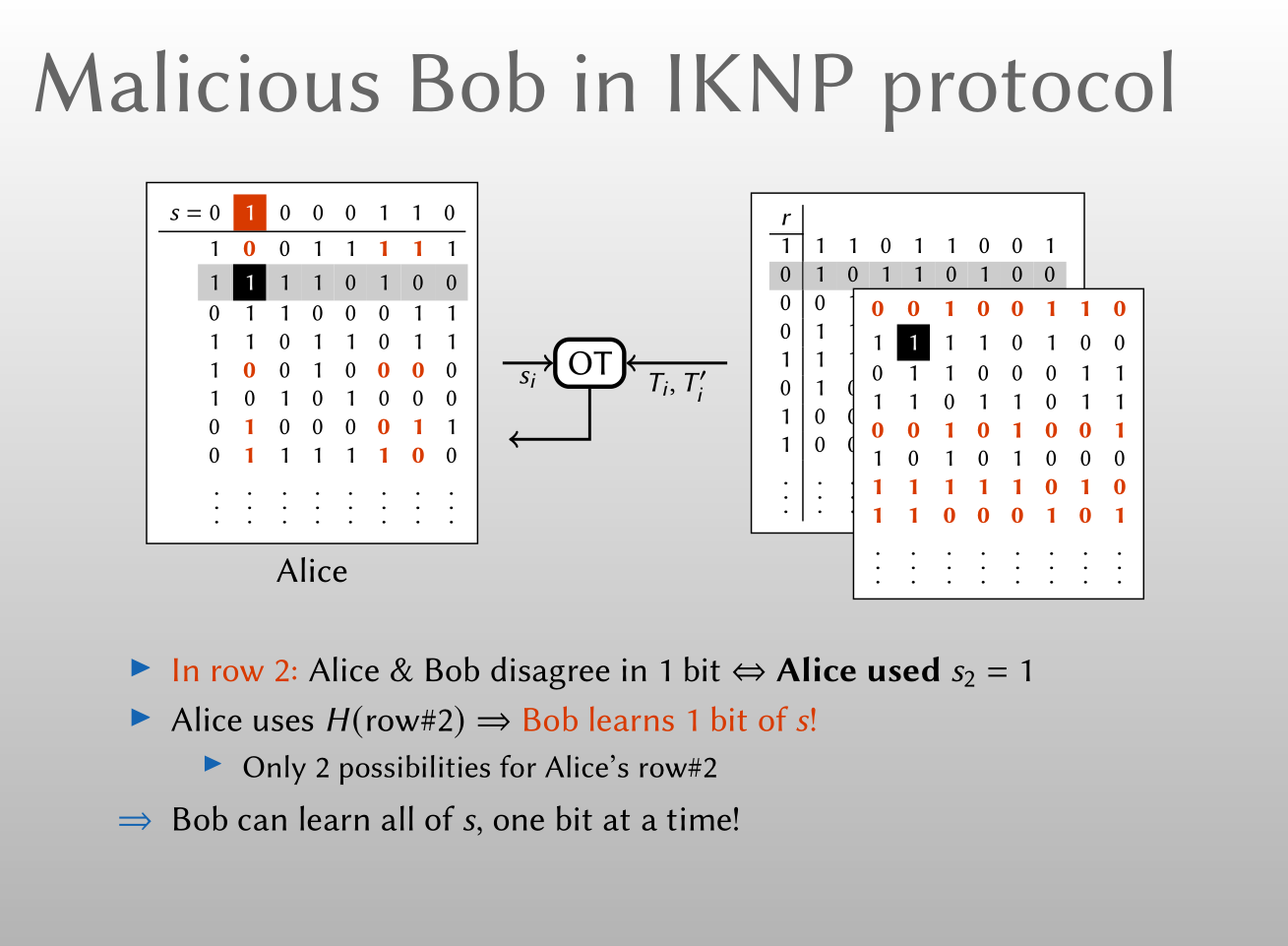
如上图所示, 假设Bob在生成选择比特矩阵时, 在第二行的图示位置篡改了其中一比特. Alice和Bob在第二行有一比特不一致, 当且仅当Alice在Base OT中输入的$s$的第二个比特$s_2=1$. 若Alice对该行进行Hash运算并在其他大型协议中使用这些结果而被Bob检测到, 则Bob将能得到$s$的一比特信息! Bob通过使用类似地方法, 在每列的不同位置篡改一个比特, 便可以获得Alice在该OT扩展协议中唯一的秘密信息$s$, 进而攻破整个OT扩展协议. 因此, IKNP协议仅是半诚实安全的.

KOS协议: 恶意安全的IKNP协议

回顾IKNP协议的等式$q_i=t_i\oplus R_i\wedge s$和恶意敌手Bob的整个攻击过程, 这是由于$R$的第$i$行$R_i$所有元素不一致造成的. 若$R_i$的汉明重量(Hamming Weight)很低, 那么Bob可以通过观察$H(q_i)$来猜测(或检查)$s$的某些比特. 那么, 如何保证Bob在协议中使用的$R_i\in\{0^n,1^n\}$呢? Keller, Orsini, Scholl发表于2015年美密会的一致性检查(Consistency check)技术⁵可以做到这一点.

如下图所示, 由于IKNP等式$q_i=t_i\oplus R_i\wedge s$对矩阵的所有行$i$都成立且所有行的$s$都相同, 因此这些行数集合组成的子集$C$所对应的式子求异或之和后该等式仍然是成立的, 即有以下等式

$$(\bigoplus_{i\in C} q_i)=(\bigoplus_{i\in C} t_i)\oplus(\bigoplus_{i\in C} R_i)\wedge s, \tag{2}$$

为此, Alice可以发起挑战, 选取随机行数组成的集合$C$发给Bob. Bob计算$t^*=\bigoplus_{i\in C}t_i, R^*=\bigoplus_{i\in C}R_i$, 并发送$t^*,R^*$给Alice作为应答. 由于Alice有$s$和$q_i$, 因此她可以计算$q^*=\bigoplus_{i\in C}q_i$, 并验证等式(2)是否成立. KOS协议的一致性检查的主要思想在于如果$R_i\in\{0^n,1^n\}$, 那么对于行的任意组合来说其异或和的结果必然也属于$\{0^n,1^n\}$这个集合; 如果存在某个$R_i$不属于这个集合, 那么Bob将有1/2的概率通过一致性检查从而作弊成功, 此外, Bob也可以通过猜测$s$使其发送的信息$t^*,R^*$通过一致性检查, 为此只需将一致性检查重复$\lambda=128$次, 如果Bob能通过所有的一致性检查, 则Alice可以认为Bob输入的$R_i$确实是属于$\{0^n,1^n\}$这个集合的. 但是, 该一致性检查技术的每次检查会泄露矩阵$R$的一比特信息, 为此Bob只需添加$\lambda=128$个额外的随机行到$R$中来盲化应答.

KOS协议针对半诚实安全的IKNP协议进行了改进, 通过引入一致性检查, 实现了恶意安全的IKNP协议. KOS协议也是目前已知最快的恶意安全的IKNP型OT扩展协议, 其通信开销几乎和半诚实安全的通信开销相同.

1-out-of-$N$ OT扩展协议

以上所介绍的OT协议都是随机2选1的OT扩展协议, 即1-out-of-2 OT extension. 下面我们考虑通过Kolesnikov和Kumaresan发表在2013年美密会的方案⁶, 从编码的角度可以将IKNP协议推广到随机1-out-of-$N$ OT扩展协议.

从编码的角度看IKNP协议

在IKNP协议中, Bob有一个选择比特串$r$, 将其扩充为一个矩阵并进行秘密共享. KK13中指出, IKNP协议将Bob选择比特扩充为矩阵的步骤, 将0映射为$0^\lambda$, 1映射为$1^\lambda$, 这是一种简单的重复码(repetition code), 如果将其视为一种纠错码, 或许我们可以采用不同的纠错码进行推广.

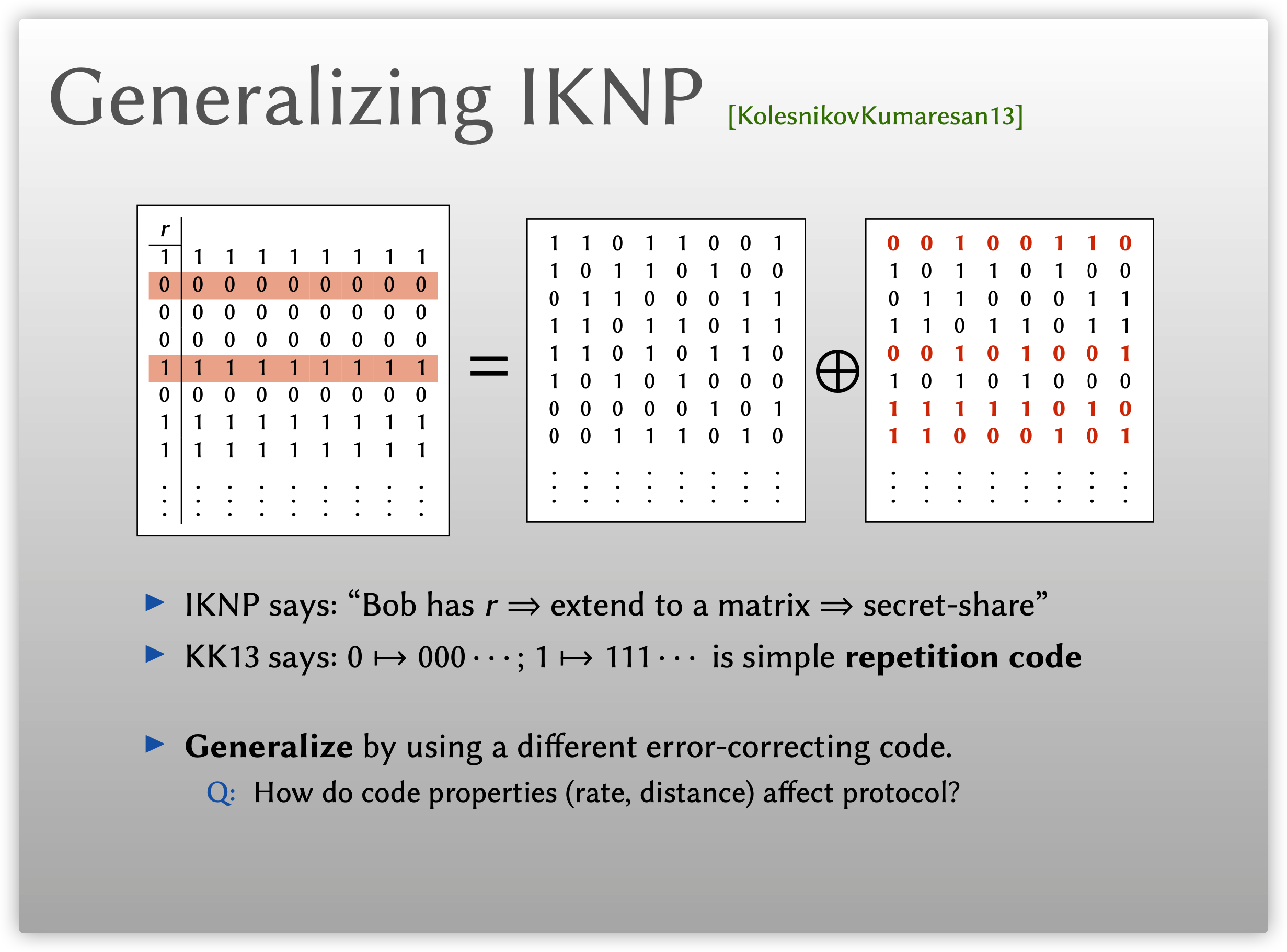
首先, 我们从编码的角度来看IKNP协议, Bob拥有选择比特串$r$, 设$C:\{0,1\}^1\to\{0,1\}^\lambda$是用于编码Bob的选择比特$r_i$的重复码, 然后对该码字矩阵进行秘密分享. 设Bob的秘密分享矩阵为$T,T'$, 则矩阵的元素可分别表示为$t_i,t_i\oplus C(r_i)$. 这样, IKNP等式(1)可以推广为如下形式

$$t_i=q_i\oplus C(r_i)\wedge s. \tag{3}$$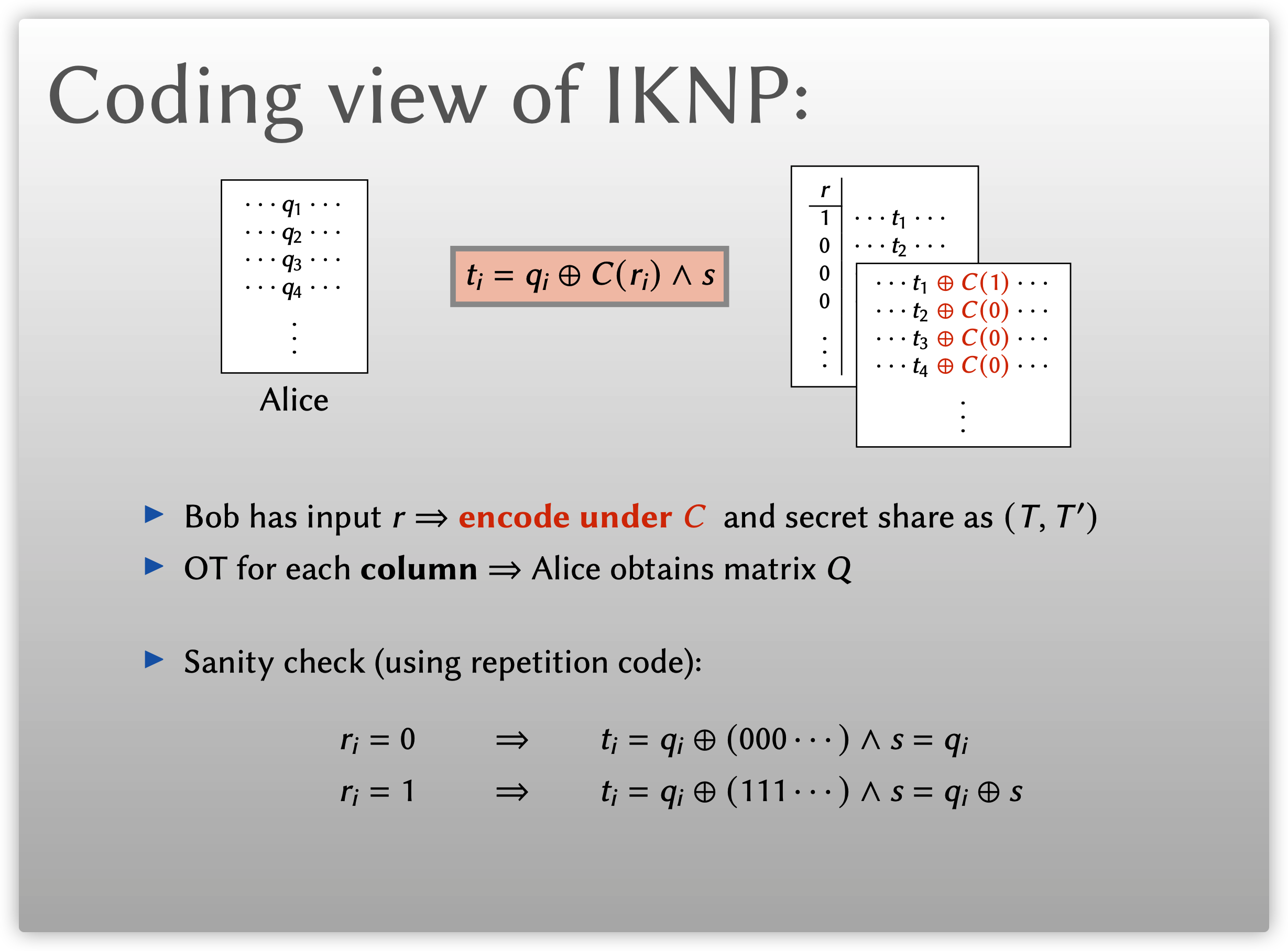

在双方执行完Base OT后, 对于矩阵的第$i$行, Bob已知$t_i$, Alice已知$q_i\oplus C(0)\wedge s$和 $q_i\oplus C(1)\wedge s.$

从Bob的视角, 利用等式(3), 可重写Alice的两个值为

$${\color{red}t_i\oplus C(r_i)\wedge s}\oplus C(0)\wedge s, \qquad{\color{red}t_i\oplus C(r_i)\wedge s}\oplus C(1)\wedge s.$$

当$C$是一个线性码时, 有$[C(a)\wedge s]\oplus[C(b)\wedge s]=C(a\oplus b)\wedge s$成立, 则Alice的两个值可以进一步写成

$$t_i\oplus{\color{red}C(r_i\oplus0)\wedge s}, \qquad t_i\oplus{\color{red}C(r_i\oplus1)\wedge s}.$$

再令$C(0)\wedge s=0^\lambda$, 则Alice的两个值进一步变为

$$t_i, \qquad t_i\oplus C(1)\wedge s,$$

两者的先后次序取决于$r_i$的具体取值.

最后, 再使用随机预言机RO来破坏重用$s$导致的关联性, 即Alice的两个值进一步变为

$$H(t_i), \qquad H(t_i\oplus C(1)\wedge s).$$

而Bob的值则变为$H(t_i)$.

IKNP协议的推广

下面我们考虑选取其他编码方案, 为了方便说明, 我们考虑一个简单编码方案: $C:\{0,1\}^3\to \{0,1\}^k$, 即此时$r_i\in\{0,1\}^3$, 总共8种取值. 对于矩阵的第$i$行, Alice可以计算8个值:

$$q_i\oplus C(000)\wedge s, q_i\oplus C(001)\wedge s,\cdots,q_i\oplus C(111)\wedge s.$$

从Bob的视角来看, 这8个值在RO模型下的形式分别为

$$H(t_i\oplus C(r_i\oplus 000)\wedge s),H(t_i\oplus C(r_i\oplus 001)\wedge s ),\cdots,H(t_i\oplus C(r_i\oplus 111)\wedge s).$$

Bob根据$r_i$的值通过Base OT可以得到$H(q_i\oplus C(r_i)\wedge s)$. 对于已知的$t$和码字$c$, Bob只知道其他值形式为$t\oplus c\wedge s$. 在RO模型中, 若所有非零码字$c_i$的汉明重量都满足大于或等于$\lambda$, 则$H(t_1\oplus c_1\wedge s),\cdots,H(t_n\oplus c_n\wedge s)$是伪随机的, 这样其他值在Bob的视角看来都是随机的, 因此可以保证方案的安全性.

KK13的文章中的一个重要结论是: 一个最小码距为$\lambda$的编码$C:\{0,1\}^\ell\to \{0,1\}^k$, 通过$k$次Base OT, 可以给出一个(随机)1-out-of-$2^\ell$的OT扩展协议, 这里的最小码距与安全性相关, 通常取为计算安全参数$\lambda$. 他们指出, 通过使用最小码距为128的Walsh-Hadamard码$C:\{0,1\}^8\to\{0,1\}^{256}$, 可以给出一个随机1-out-of-256 OT扩展协议, 这是一个半诚实安全的协议.

此外, Orru, Orsini和Scholl于2016年的工作中⁷指出, 通过使用最小码距为171的BCH码$C:\{0,1\}^{76}\to \{0,1\}^{512}$, 可以给出一个随机1-out-of-$2^{76}$ OT扩展协议, 他们同时给出了半诚实安全和恶意安全下的版本.

同年的CCS会议上, Kolesnikov, Kumaresan, Rosulek和Trieu的工作⁸中指出, 在半诚实模型下, 我们不需要编码$C$的线性性质, 由于协议过程不需要译码, 因此也不需要$C$的纠错性质, 而只要$C$能以压倒性概率保证汉明重量大于等于计算安全参数即可, 因此可以使用任意输入长度的伪随机函数$C:\{0,1\}^{\color{red} *}\to \{0,1\}^{\sim480}$来取代编码$C$, 这样, 我们可以构造一个半诚实安全的随机$\infty$-out-of-1 OT扩展协议, 这里的伪随机函数$C$也被称为伪随机编码(Pseudo-Random Code, PRC).

性能比较

以下是1-out-of-2和1-out-of-$N$ OT扩展协议在不同安全模型下的对比. 结论: OT是廉价的!

相关代码参见Github: osu-crypto/libOTe: A fast, portable, and easy to use Oblivious Transfer Library (github.com).

参考文献

1. Russell Impagliazzo, Steven Rudich. Limits on the Provable Consequences of One-Way Permutations. STOC'89. ↩

2. Donald Beaver. Efficient Multiparty Protocols Using Circuit Randomization. CRYPTO 1991. ↩

3. Donald Beaver. Correlated pseudorandomness and the complexity of private computations. STOC'96. ↩

4. Yuval Ishai, Joe Kilian, Kobbi Nissim, Erez Petrank. Extending Oblivious Transfers Efficiently. CRYPTO 2003. ↩

5. Marcel Keller, Emmanuela Orsini, Peter Scholl. Actively Secure OT Extension with Optimal Overhead. CRYPTO 2015. ↩

6. Vladimir Kolesnikov, Ranjit Kumaresan. Improved OT Extension for Transferring Short Secrets. CRYPTO 2013. ↩

7. Michele Orrù, Emmanuela Orsini, Peter Scholl. Actively Secure 1-out-of-N OT Extension with Application to Private Set Intersection. CT-RSA 2017. ↩

8. Vladimir Kolesnikov, Ranjit Kumaresan, Mike Rosulek, Ni Trieu. Efficient Batched Oblivious PRF with Applications to Private Set Intersection. CCS'16. ↩

本文标题: 不经意传输及其优化方案
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16237676401097.html
本站文章采用 知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间: 2021-06-15T22:34:00+08:00