混淆电路及其优化方案
本文整理了美国俄勒冈州立大学电子工程和计算机科学学院副教授Mike Rosulek关于安全多方计算与混淆电路的演讲主题的主要内容, 文中图片均来源于Mike Rosulek的演讲报告幻灯片, 请查看文末相关链接中Mike Rosulek的个人主页获取报告文件1. 整理如有错误之处, 恳请批评指正, 谢谢!
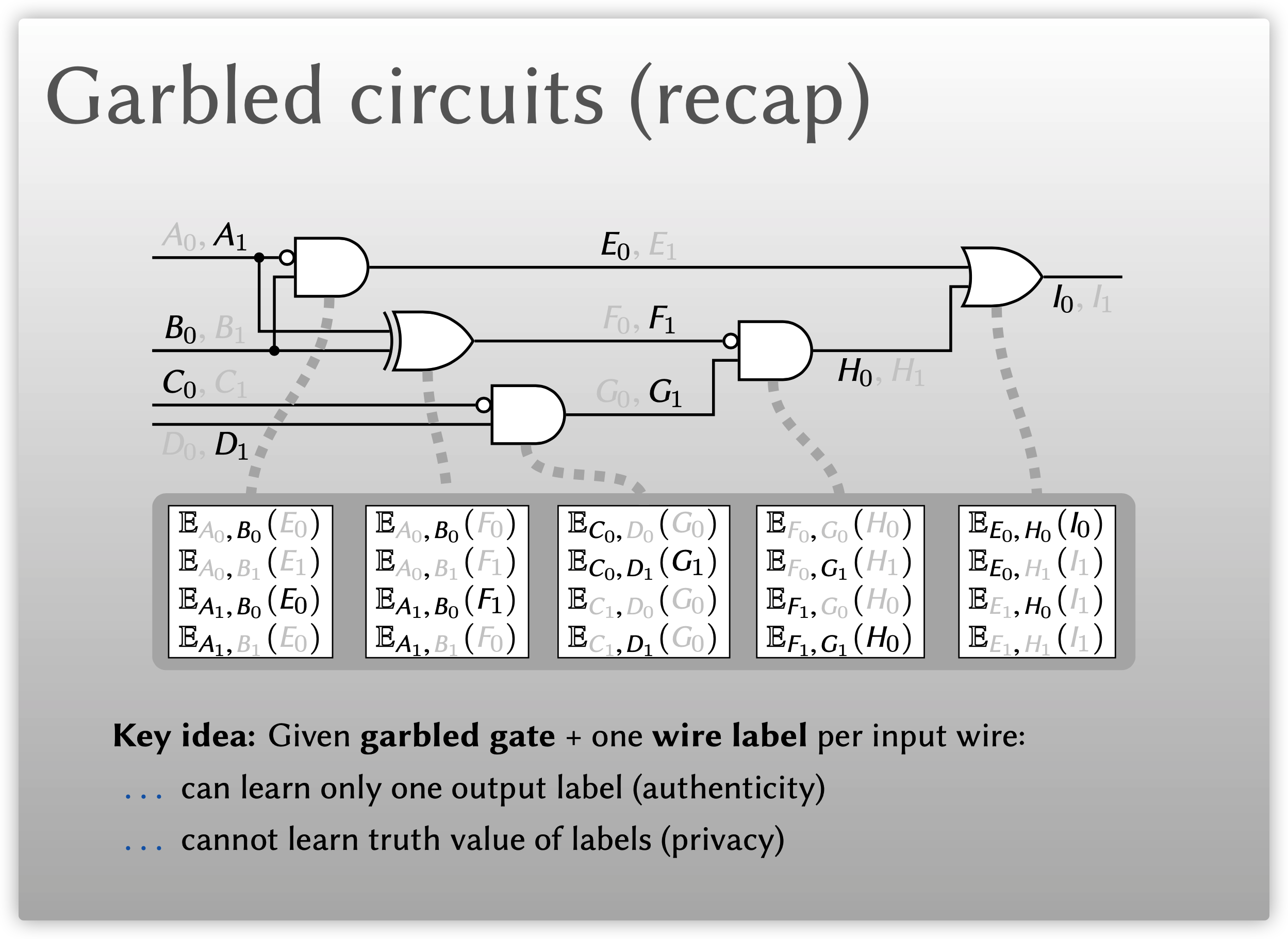
首先概述一下混淆电路的基本步骤. 对于电路的每条线路, 我们随机选取两个密钥, 称为线路标签(wire label), 分别对应于线路的输入True(1)和False(0), 但标签都是随机选取的, 因此只看标签无法辨认真值. 对于所有的门和电路, 我们使用标签加密它的真值表, 例如下图的第一个门中, 输入为1和0, 结果为0, 使用标签\(A_1,B_0\)来加密\(E_0\). 每个门都有4个密文, 所有门的这些密文即称为混淆电路. 电路生成者Garbler生成混淆电路, 因此他知道所有的标签和所有的线路, 他发送混淆电路给电路计算者Evaluator. 电路计算者只知道输入线路标签的其中之一, 称为混淆输入. 电路计算者计算电路将得到混淆输出标签的其中之一, 除了最终输出线路之外, 他无法获知该标签所对应的真值. 给定一个混淆门和每条输入线路的其中一个线路标签, 安全性主要基于以下两点:
- 仅能获得一个输出标签(可靠性);
- 无法获知标签的真值(隐私性).
混淆电路的优化
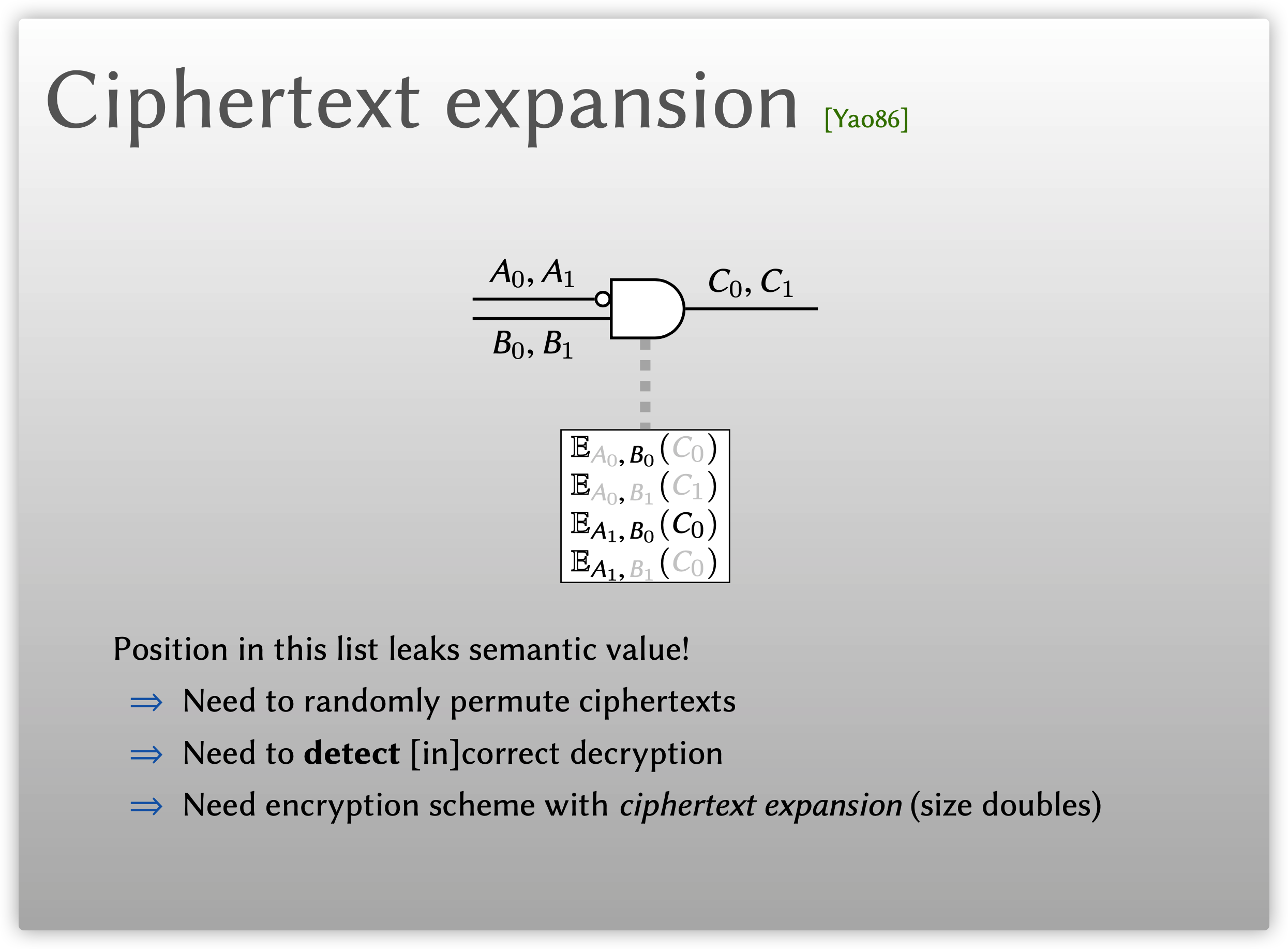
混淆电路的计算是非常快速的, 比如使用硬件AES来计算, 因此计算通常不是一个问题. 混淆电路的大小在实际应用中是一个很重要的参数, 混淆电路的门数越多, Garbler需要发送密文的数量也越大, 通信量也越大, 因此混淆电路在应用中通常受限于网络. 下面将主要介绍混淆布尔电路在通信量方面的优化方案.
Ciphertext expansion
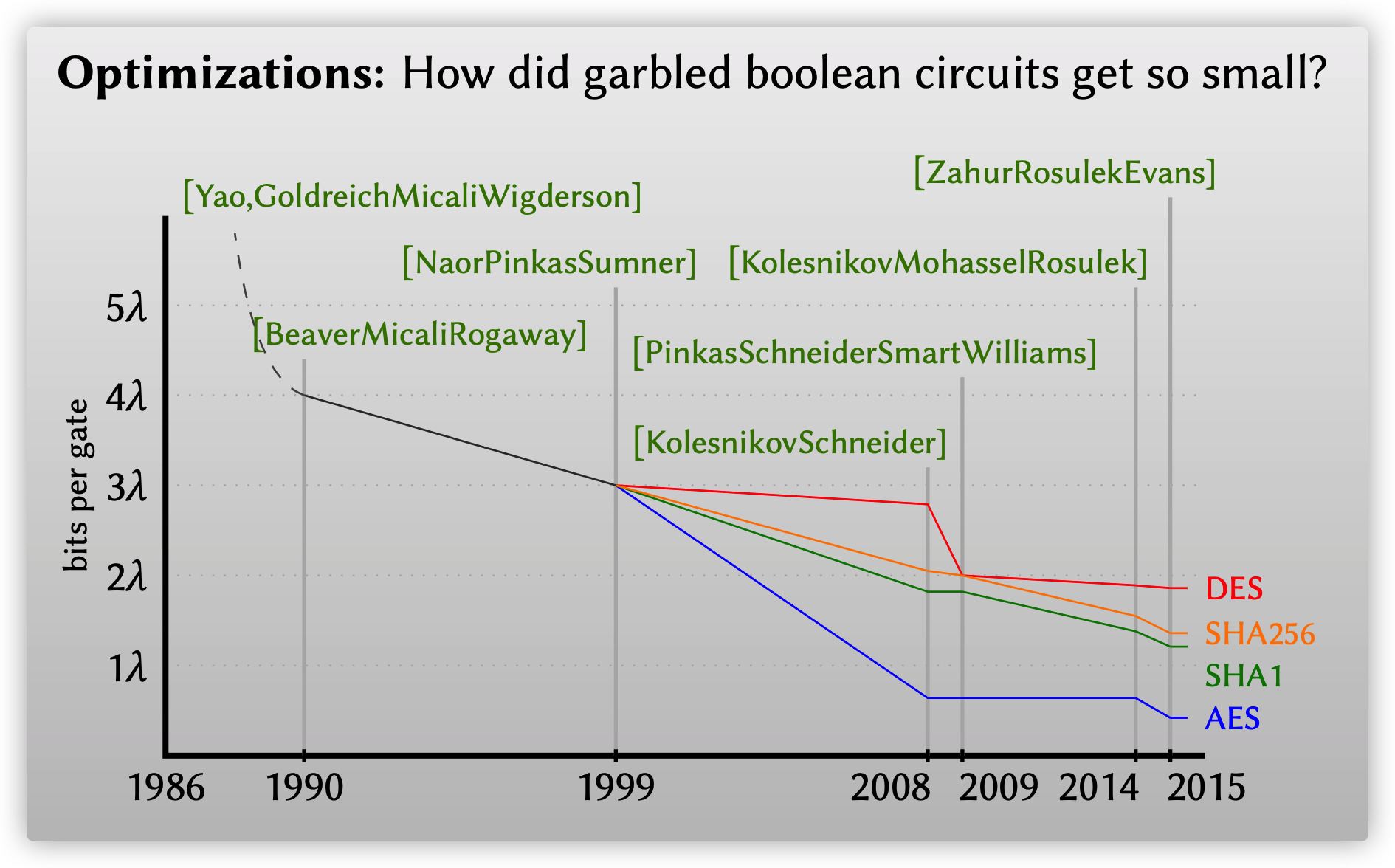
如果密文的排列是按照输入真值按规律排列的, 则密文在列表中的位置可能会泄漏输入的语义真值. 为此, 我们需要通过随机置换来打乱密文的位置. 在之前的描述中, 我们总是假设Evaluator知道哪个密文可以成功解密出正确的标签. 那么在实际应用中, 当Evaluator使用收到的加密标签来解密四个密文时, Evaluator如何判断密文的解密成功还是失败? 例如, 我们知道使用\(A_0,B_1\)可以成功解密\(C_0\), 但对于Evaluator来说, 他并不能判断四个结果中, 哪一个是正确的标签\(C_0\), 因为解密的结果都是随机字符串. 这个问题也是限制混淆电路效率的原因之一, 因为多余的解密需要额外的开销.
一种可行的解决方案是使用密文扩展(Ciphertext expansion)方案2, 通过加入额外的冗余信息如MAC等, 使得密文长度比输出线路标签长. 例如, 如果输出线路的标签是128比特的, 则可能需要256比特的密文, 这样所有的这些密文都将具有256比特的长度. 但是, 这样做将影响解密效率, 不实用.
Point-and-permute
下面介绍由Beaver等人在1990年提出的Point-and-permute技术3, 可以让Evaluator根据得到的加密标签直接获知应该解密哪一个密文获得正确的标签, 既不需要试解密, 也不需要再做密文扩展. 如下图所示, Point-and-permute的主要思想是在每个线路标签上附一个随机颜色比特(color bit, 或称为置换比特permutation bit), 图中分别用红色和蓝色指代不同的颜色比特, 然后根据加密标签的颜色比特来排列密文的位置. 需要注意的一点是, 每条线路颜色比特与加密标签所对应的真值之间的关系是随机的, 两者并无直接关系, 例如, 输入线路上的红色比特在\(A_0\)上对应于输入真值为0, 但\(B_1\)上对应的则是1.

下图中的混淆真值表是根据输入线路的颜色比特来排列的, 代表了不同的密文相应的位置. 通常将输入标签的最后一比特设置为颜色比特. 这样一来, Evaluator可以通过观察输入线路标签的颜色比特便可获知他该解密哪个密文得到正确的标签. 例如, 假设Evaluator获得的加密标签分别为\(A_1, B_1\), 分别对应的颜色比特为蓝色、红色, 于是Evaluator直接解密第三个密文即可得到正确的标签. 如果存在一个随机预言机\(\mathsf H\), 则我们可以使用简单的一次加密来执行混淆电路的加密, 即\(\mathbb{E}_{A,B}(C)=\mathsf H(A,B)\oplus C\). 在实际应用中, \(\mathsf H\)可以使用固定密钥AES(fixed-key AES)来实例化. 通过Point-and-permute方案, 可以将Evaluator的解密计算量降低4倍.

Garbled Row Reduction 3
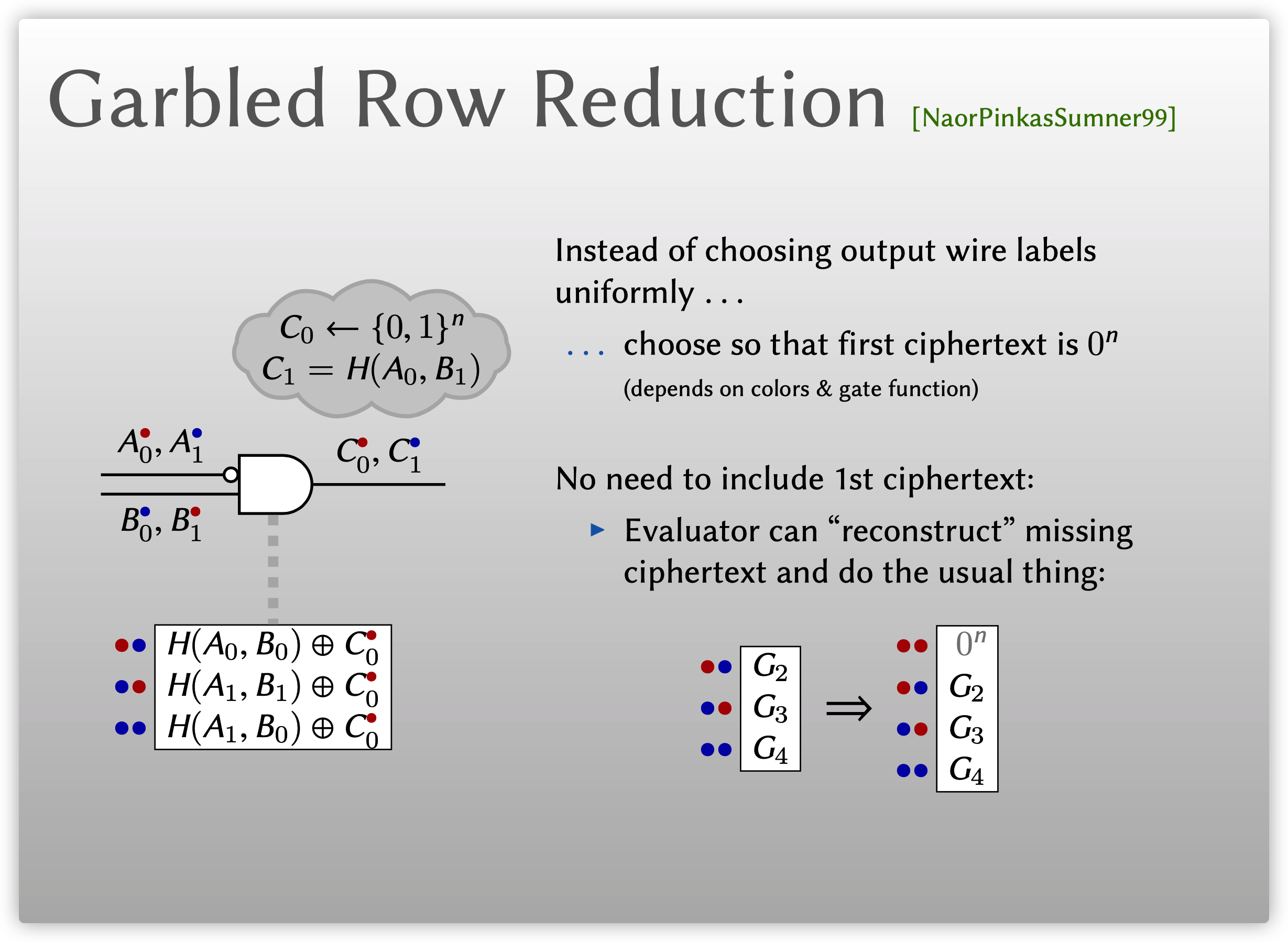
之前的描述中, 我们总是假设Garbler在每条线路上的两个标签都是随机选取的. 1999年, Naor等人的工作中4考虑了这样一个技巧: 不再随机选取输出线路的两个加密标签, 而是选取合适的输出线路加密标签使得混淆表的第一个密文(取决于颜色比特和门函数)总为特殊值\(0^n\), 而另一个加密标签仍然随机选取. 例如, 在下图中, 混淆表的第一行为\(\mathsf{H}(A_0,B_1)\oplus C_1\), 则直接取\(C_1=\mathsf{H}(A_0,B_1)\)即可使得混淆表的第一行密文为零串\(0^n\). 这样Garbler就不再需要发送第一个密文了, 从而将Garbler在每个门的密文发送的数量从4个减少为3个, Evaluator可以"重构"出第一个密文, 然后正常解密即可得到正确的标签. 通常把这种技术记为GRR3. 第一个密文取特殊值并不会影响混淆电路的安全性, 这是因为Evaluator无法有效区分剩下的三个密文到底是针对真值0的加密标签还是1的加密标签.
Free XOR
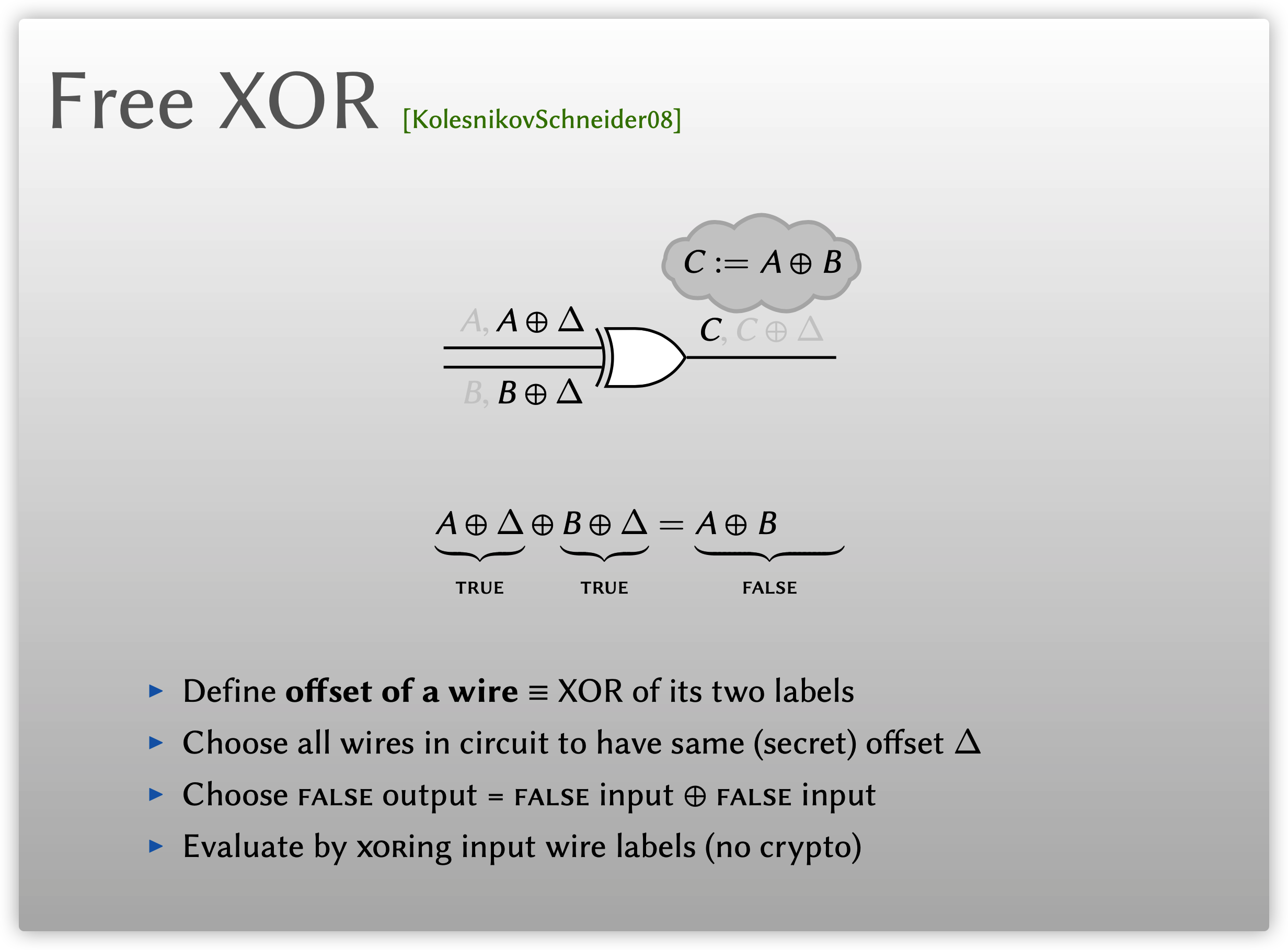
Free XOR技术5由Kolesnikov和Schneider于2008年提出, 该方案针对XOR门进行优化, 使得XOR混淆时, 不再需要发送密文, 也无需进行加解密运算, 从而将XOR门参与方的开销降为0. 之前的方案的标签可以看成如下形式: 定义XOR门线路\(W\)的偏移量(offset)\(\Delta_W\)为该线路两个标签的XOR, 则任意一条线路的两个标签都可以表示为\((W,W\oplus\Delta_W)\), 其中\(W\)是随机选取的. Free XOR技术是指将XOR门的所有输入线路的偏移量都取为同一个\(\Delta\), 而输出线路标签则取为两个输入线路标签的XOR. 如下图中, 设\(A,B\)分别表示两条输入线路上真值为FALSE的标签, \(C\)表示输出线路上真值为FALSE的标签, 则输入线路的标签可分别表示为\((A,A\oplus \Delta),(B,B\oplus\Delta)\), 而输出标签可表示为\((C,C\oplus\Delta)=(A\oplus B,A\oplus B\oplus\Delta)\). 如此一来, Garbler无需加密输出标签, 而Evaluator计算输出标签只需将收到的输入标签直接XOR在一起即可, 无需任何解密运算, 即XOR门的计算是免费的(free). 原论文中指出Free XOR在Random Oracle(RO)模型下, 对半诚实敌手来说是安全的. 此外, Free XOR技术与GRR3技术是兼容的, 可以一起使用.
Garbled Row Reduction 2
在前面的Garbled Row Reduction小节中, 我们通过选取一个合适的输出标签, 使得第一行密文为全零, 从而不再需要发送第一个密文, 降低了Garbler的通信开销, 注意到在这里的另一个输出标签仍然是随机选取的, 能否在此基础上进一步减少密文发送的数量呢? 答案是肯定的, 只需两个密文的AND门优化方案最早在2009年由Pinkas等人6给出, 但由于其使用了多项式插值, 因此方案较复杂, 这里不做介绍. 下面将主要介绍CCS'15会议上Gueron等人的优化方案7, 其核心思想是对于AND门, 可以通过选取合适的另一个输出标签, 使得剩下的三个密文XOR在一起结果是全零.
如下图所示, 通过选取\(C_1=\mathsf{H}(A_0,B_1)\overset{\Delta}{=}\mathsf{H}_{01}\)使得第一行密文全为零, 通过选取\(C_0=\mathsf{H}_{00}\oplus\mathsf{H}_{11}\oplus\mathsf{H}_{10}\), 容易验证这将使剩下三行密文的XOR结果为零.
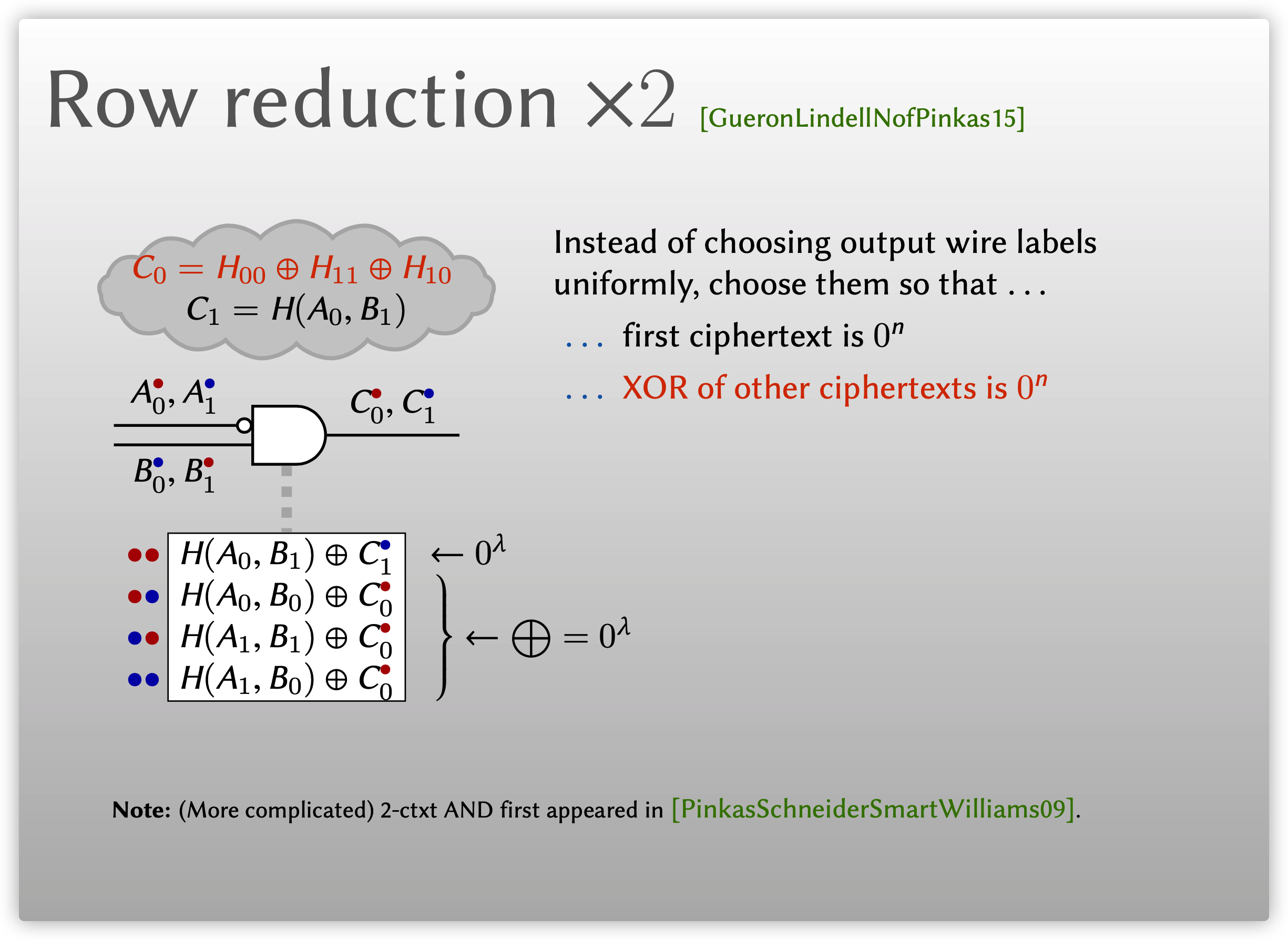
如果Garbler和Evaluator商定使用上述方式生成电路, 则可以将Garbler发送密文的个数从4个下降到2个, 即Garbler不再需要发送前两个密文, 只需发送第三个和第四个即可, 第二个密文为第三个密文与第四个密文的XOR结果, 如下图所示, 这种技术被称为GRR2. 需要注意的是这种优化方案只针对于像AND门这样的类型, 因为需要保证有真值表中有三个输出相同. 如果真值表中两个输出为1, 两个为0, 则这种方法就失效了, 因为此时三个密文的XOR结果不能相互抵消.

根据实际电路的不同, Free XOR技术和GRR2各有优势, 但这两种技术是不兼容的, 因为Free XOR要求两个输出标签必须满足\(C_0\oplus C_1=\Delta\), 但GRR2中对两个输出标签的要求无法保证同时也能满足Free XOR的这个要求.
Half-gates
2015年的欧密会上Zahur、Rosulek和Evans等人提出了Half-gates技术8, 不仅可以实现XOR门不需要密文(free), 同时AND门只需2个密文.
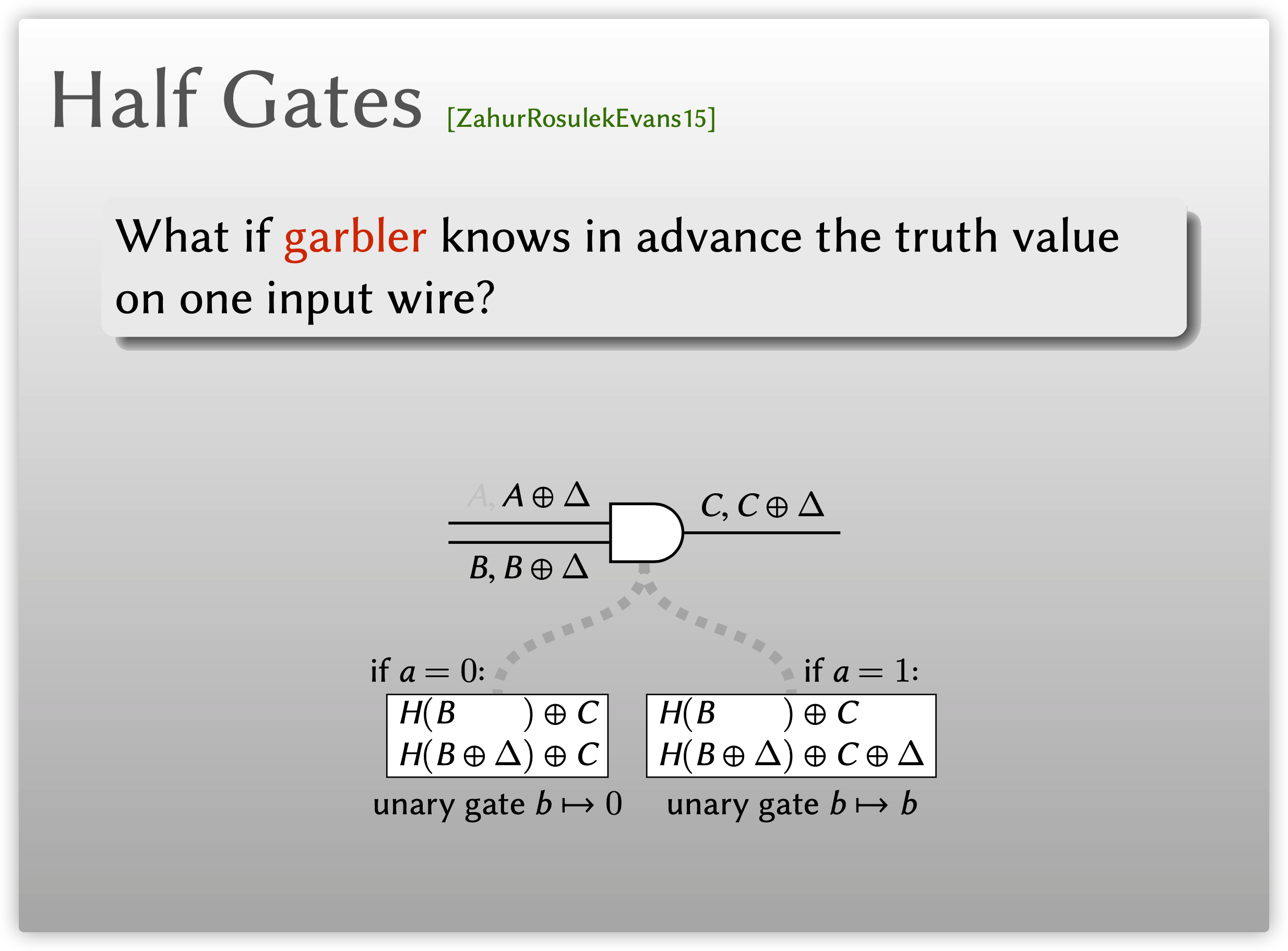
考虑类似于Free XOR标签设定的AND门, 设\(\Delta\)为标签偏移量(offset), 上侧输入标签分别为\(A, A\oplus \Delta\), 分别对应真值\(0,1\), 下侧输入标签\(B, B\oplus \Delta\), 分别对应真值\(0,1\), 输出标签分别为\(C,C\oplus\Delta\), 分别对应真值\(0,1\), 为方便描述, 在下文中输入线路的真值分别记为\(a,b\), 输出线路的真值记为\(c\), 我们分别考虑以下三个问题:
- 假设Garbler事先通过某种方式知道上侧线路输入\(a\)及其对应的标签, 如何计算\(c=a\wedge b\)?
-
若\(a=0\), 对应于标签\(A\), 由AND门的性质, 我们有输出线路的真值\(c\equiv 0\), 与\(b\)的取值无关, Garbler可以和往常一样加密输出标签, 使用\(B\)来加密\(C\), 使用\(B\oplus \Delta\)来加密\(C\), 此时输出标签表示为\(\mathsf{H}(B)\oplus C, \mathsf{H}(B\oplus \Delta)\oplus C\);
-
若\(a=1\), 对应于标签\(A\oplus\Delta\), 由AND门的性质, 我们有\(c=b\), Garbler只需使用\(B\)来加密\(C\), 使用\(B\oplus \Delta\)来加密\(C\oplus \Delta\), 此时输出标签表示为\(\mathsf{H}(B)\oplus C, \mathsf{H}(B\oplus \Delta)\oplus C\oplus \Delta\).
容易看出, 以上两种情况可以合并为Garbler使用\(B\)来加密\(C\), 使用\(B\oplus \Delta\)来加密\(C\oplus a\Delta\), 两个输出标签可表示为\(\mathsf{H}(B)\oplus C\)和\(\mathsf{H}(B\oplus \Delta)\oplus C\oplus a\Delta\), 于是混淆表的密文数为2. Garbler使用Point-and-permute技术, 根据\(B\)的颜色比特适当地排列密文的次序. 我们可以进一步使用Garbled Row Reduction的技巧来减少密文数, 即不再均匀随机选取\(C\), 而是取\(C:=\mathsf{H}(B)\), 使得混淆表第一个密文为全零, 于是Garbler只需发送第二个密文即可.
这说明, 如果Garbler事先通过某种方式知道AND门的一个输入\(a\)及其对应的标签, 则他只需发送一个密文\(\mathsf{H}(B\oplus \Delta)\oplus C\oplus a\Delta\), 即可混淆计算AND门. 称这种情况下的AND门为Garbler-half-gate, 它包含一个密文, Garbler调用\(\mathsf{H}\)两次, Evaluator调用\(\mathsf{H}\)一次.
- 假设Evaluator事先通过某种方式获知下侧线路的真值\(b\)及其对应的输入标签, 如何计算\(c=a\wedge b\)?
-
若Evaluator知道\(B\)及其所对应的真值为\(b=0\), 则Evaluator须得到\(c=0\)的输出标签\(C\), Garbler只需使用\(B\)来加密\(C\)的结果作为密文, 即\(\mathsf H(B)\oplus C\);
-
若Evaluator知道\(B\oplus \Delta\)及其所对应的真值为\(b=1\), 此时需要将上侧输入线路的标签转移到输出线路的标签上, 使得当上侧标签为\(A\)时, Evaluator得到的输出标签为\(C\), 当上侧标签为\(A\oplus \Delta\)时, Evaluator得到的输出标签为\(C\oplus \Delta\), 怎么做呢? 只需将上侧标签直接与\(A\oplus C\)进行XOR即可. 于是Garbler只需用\(B\)来加密\(C\), 用\(B\oplus \Delta\)来加密\(A\oplus C\)的结果作为密文, 即输出标签为\(\mathsf{H}(B)\oplus C,\mathsf{H}(B\oplus\Delta)\oplus A\oplus C\). 注意, 这种情况下Garbler不再使用Point-and-permute技术置换密文的次序, 这是因为Evaluator已经知道了\(b\),可以根据\(b\)的取值来判断需要解密哪个密文, 如果\(b=0\), 则解密第一个密文, \(b=1\), 则解密第二个密文. 但仍可以使用Garbled Row Reduction的技巧来减少密文数, 即取\(C:=\mathsf{H}(B)\), 使得混淆表第一个密文为全零, 于是Garbler只需发送第二个密文即可.
这说明Evaluator如果事先通过某种方式获知下侧线路的真值\(b\)及其对应的输入标签, Garbler只需发送一个密文即可混淆计算AND门. 下文中, 称这种情况下的AND门为Evaluator-half-gate, 它包含一个密文, Garbler调用\(\mathsf{H}\)两次, Evaluator调用\(\mathsf{H}\)一次.

- 现在抛开以上两种假设, \(a,b\)分别是Gabler, Evaluator的秘密, 如何计算\(c=a\wedge b\)?
首先, 将\(c=a\wedge b\)分解成如下图所示的形式, Garbler均匀随机选择一个比特\(r\)用于盲化\(a\), 并让Evaluator获得\(a\oplus r\), 这样做不会泄漏\(a\)的语义真值, 因为这相当于一次一密(OTP). Evaluator已知\(a\oplus r\), 可以通过调用一个Evaluator-half-gate来计算分解式中的\((a\oplus r)\wedge b\), 而Garbler已知\(r\), 可以通过调用一个Garbler-half-gate来计算\(r\wedge b\), 最后将两个half-gate的结果通过一个XOR门计算即可, 而XOR门计算是免费的, 于是计算\(c=a\wedge b\)总的开销仅为2个密文, Garbler调用\(\mathsf{H}\)四次, Evaluator调用\(\mathsf{H}\)两次.
那么, Garbler如何选择\(r\), 又如何让Evaluator获得\(a\oplus r\)呢? 实际上, Garbler只需将\(r\)取为真值为0(FALSE)的标签\(A\)的颜色比特即可做到这一点, 而无需任何额外开销, 此时, \(a\oplus r\)为Evaluator所收到的标签\(A\)或\(A\oplus \Delta\)的颜色比特.
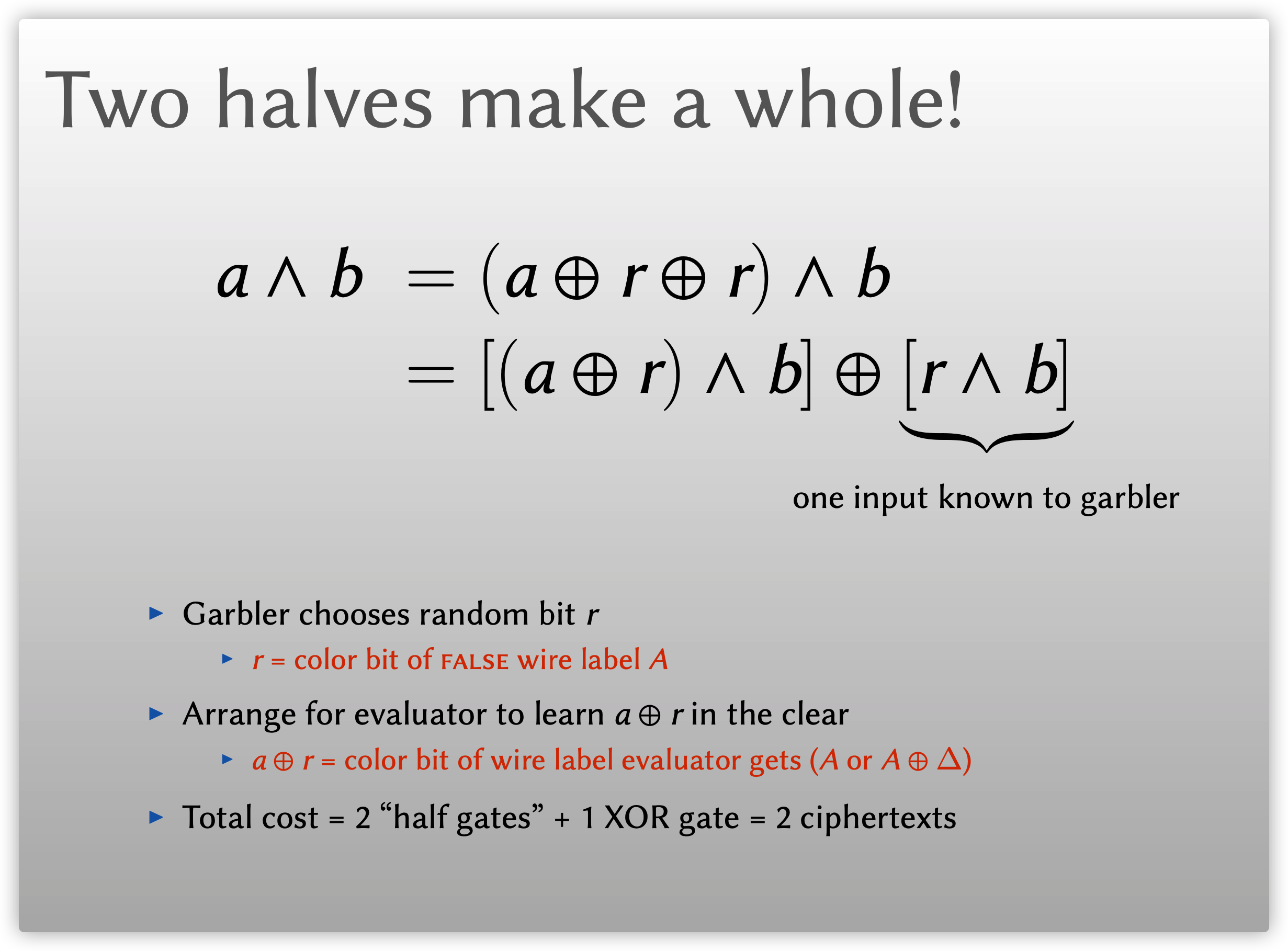
开销比较
下图展示了上述方案与原始的混淆电路方案相比, 密文大小与Garbler和Evaluator的平均计算开销, 其中\(\lambda\)表示安全参数. 注意到原始混淆电路中每个门理论上只需4个密文, 但由于需要进行Ciphertext expansion, 因此, 这实际上相当于需要8个密文.
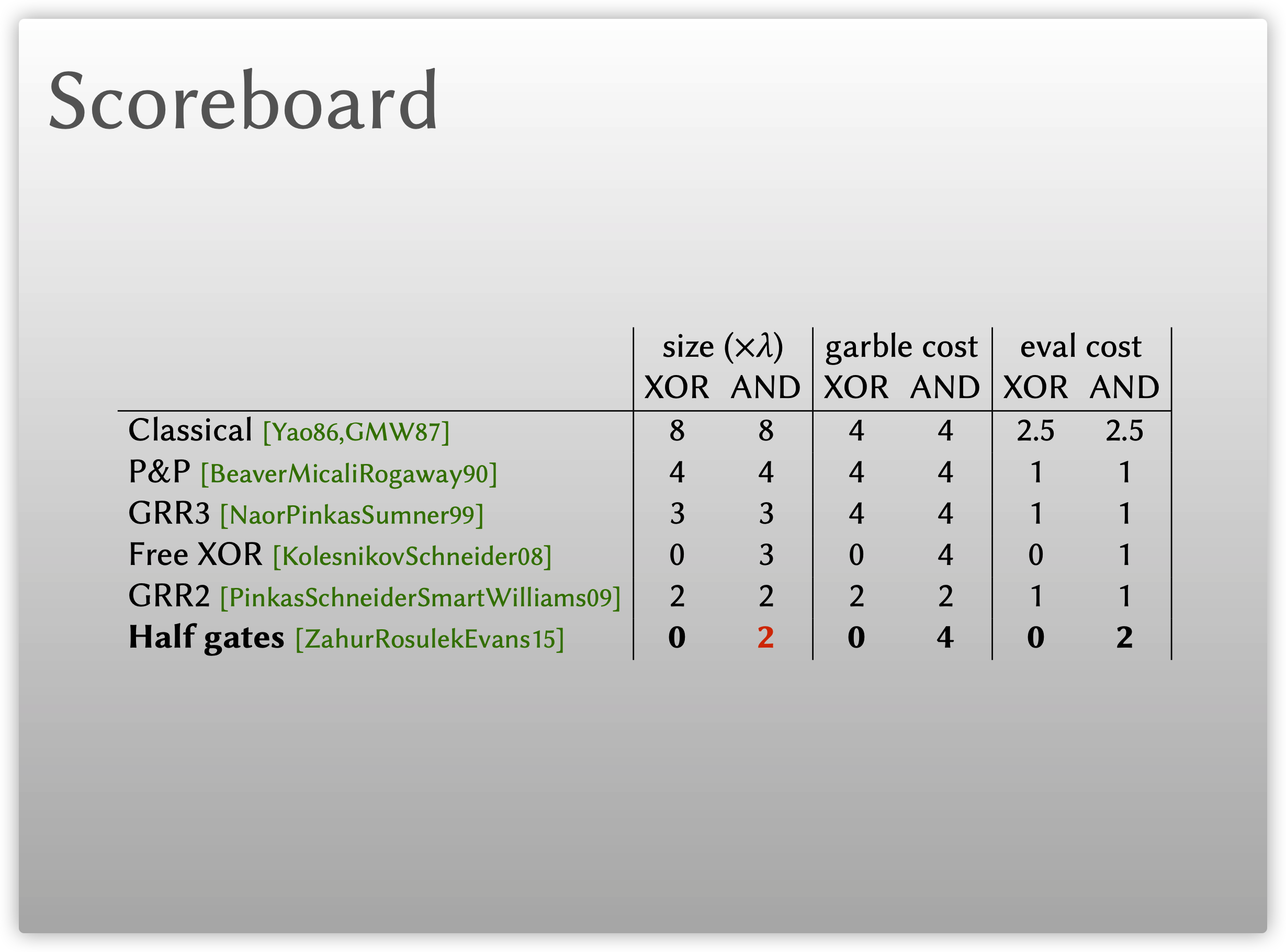
易见, Half-gates技术是当前混淆电路中的最佳优化方案. 很自然的一个问题, 我们能否可以做到比Half-gates技术更好? Half-gates的作者在他们的文章中指出, 如果仅使用标准技术(Standard techniques), 在通用模型下不能以少于两个密文来混淆计算一个AND门. 虽然在CCS'16会议Ball等人9和16年亚密会Kempka等人10的两项工作中指出可以仅以一个密文来计算AND门, 但都基于特殊假设, 如整个电路只有一个AND门等, 在大规模电路中不适用. 因此, 能否在通用模型下做到比Half-gates方案更好, 仍然是一个公开问题.
相关链接与参考文献
-
Mike Rosulek的个人主页: http://web.engr.oregonstate.edu/~rosulekm/ ↩
-
Yao, Andrew Chi-Chih. “How to Generate and Exchange Secrets.” 27th Annual Symposium on Foundations of Computer Science (Sfcs 1986), 1986, pp. 162–167. ↩
-
Beaver, Donald et al. “The Round Complexity of Secure Protocols (Extended Abstract).” STOC 1990 (1990). ↩
-
Naor, M. et al. “Privacy preserving auctions and mechanism design.” EC '99 (1999). ↩
-
Kolesnikov, V. and T. Schneider. “Improved Garbled Circuit: Free XOR Gates and Applications.” ICALP (2008). ↩
-
Pinkas, Benny et al. “Secure Two-Party Computation is Practical.” IACR Cryptol. ePrint Arch. (2009). ↩
-
Gueron, S. et al. “Fast Garbling of Circuits Under Standard Assumptions.” Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security (2015). ↩
-
Zahur, Samee et al. “Two Halves Make a Whole - Reducing Data Transfer in Garbled Circuits Using Half Gates.” EUROCRYPT (2015). ↩
-
Ball, Marshall et al. “Garbling Gadgets for Boolean and Arithmetic Circuits.” Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (2016). ↩
-
Kempka, Carmen, et al. “How to Circumvent the Two-Ciphertext Lower Bound for Linear Garbling Schemes.” Proceedings, Part II, of the 22nd International Conference on Advances in Cryptology --- ASIACRYPT 2016 - Volume 10032, vol. 2017, 2016, pp. 967–997. ↩
本文标题: 混淆电路及其优化方案
本文作者: 云中雨雾
本文链接: https://weiviming.github.io/16222891373334.html
本站文章采用 知识共享署名4.0 国际许可协议进行许可
除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间: 2021-05-29T19:52:17+08:00